Límite de Fermat: en qué consiste y ejercicios resueltos
El límite de Fermat es un método numérico utilizado para conseguir el valor de la pendiente de una recta, la cual es tangente a una función en un punto determinado de su dominio. También es empleado en la obtención de puntos críticos de una función. Su expresión se define como:
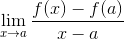
Es obvio que Fermat desconocía los fundamentos de la derivación, sin embargo fueron sus estudios los que impulsaron a un grupo de matemáticos a indagar sobre las rectas tangentes y sus aplicaciones en el cálculo.
Índice del artículo
- 1 ¿En qué consiste el límite de Fermat?
- 2 Aplicación del límite de Fermat para máximos y mínimos
- 3 Historia
- 4 Ejercicios
- 5 Referencias

Consiste en un acercamiento de 2 puntos, que en condiciones anteriores forman una recta secante a la función con intersección en pares de valores.
Al aproximar la variable al valor “a”, se obliga al par de puntos a encontrarse. De esta forma la recta anteriormente secante, se convierte en tangente al punto ( a ; f(a) ).
El valor del cociente ( x – a ), al ser evaluado en el punto “a”, arroja una indeterminación de límites del tipo K entre cero ( K/0 ). Donde a través de distintas técnicas de factorización se pueden romper dichas indeterminaciones.
Las técnicas de operación más utilizadas son:
-Diferencia de cuadrados ( a2 – b2 ) = ( a + b ) ( a – b ) ; La existencia del elemento (a–b) implica en gran parte de los casos el factor que simplifica la expresión (x–a) en el cociente del límite de Fermat.
– Completación de cuadrados ( ax2 + bx ); Tras completar cuadrados se obtiene un binomio de Newton, donde uno de sus 2 factores se simplifica con la expresión ( x – a ), rompiendo la indeterminación.
– Conjugada ( a + b ) / ( a + b ); Multiplicar y dividir la expresión por la conjugada de algún factor, puede ser de gran ayuda para romper la indeterminación.
– Factor común; En muchos casos el resultado de operar el numerador del límite de Fermat f(x) – f(a) oculta al factor ( x – a ) necesario para factorizar. Para esto se observa con detenimiento qué elementos se repiten en cada factor de la expresión.
Aún cuando el límite de Fermat no diferencia entre máximos y mínimos, ya que solo puede identificar los puntos críticos según su definición, es comúnmente usado en el cálculo de topes o pisos de las funciones en el plano.
Un conocimiento base sobre la teoría gráfica de funciones en conunto con este teorema, puede ser suficiente para establecer valores máximos y mínimos entre funciones. De hecho los puntos de inflexión pueden ser definidos mediante el teorema del valor medio adicional al teorema de Fermat.
La paradoja más significativa para Fermat llegó al estudiar la parábola cúbica. Debido a que su atención estaba dirigida a las rectas tangentes de una función para un punto dado, se encontró con el problema de definir dicha recta tangente en el punto de inflexión existente en la función.
Parecía imposible determinar la recta tangente a un punto. Comienza así la indagación que daría origen al cálculo diferencial. Definido luego por importantes exponentes de la matemática.
El estudio de máximos y mínimos de una función supuso un reto para las matemáticas clásicas, donde hacía falta un método inequívoco y práctico para la definición de estos.
Fermat creó un método basado en la operación de pequeños valores diferenciales, los cuales tras procesos de factorización, son eliminados dando paso al valor buscado como máximo y mínimo.
Esta variable habrá de ser evaluada en la expresión original para determinar la coordenada de dicho punto, que junto a criterios analíticos será definido como máximo o mínimo de la expresión.
En su método, Fermat emplea el simbolismo literal de Vieta, que consistía en el uso exclusivo de letras mayúsculas: Las vocales, para las incógnitas, y las consonantes para las cantidades conocidas.
Para el caso de valores radicales, Fermat implementó un proceso particular, que más adelante sería utilizado en las factorizaciones de los límites de indeterminación infinito entre infinito.
Este proceso consiste en dividir cada expresión entre el valor del diferencial utilizado. En el caso de Fermat utilizó la letra E, donde tras la división entre la mayor potencia de E, el valor buscado del punto critico se vuelve despejable.
El límite de Fermat es de hecho uno de los aportes de menos renombre en la larga lista del matemático. Sus estudios fueron desde los números primos, hasta básicamente crear las bases para el cálculo.
A su vez Fermat era conocido por sus excentricidades respecto a sus hipótesis. Era común que dejara una especie de reto a los otros matemáticos de la época, cuando él ya poseía la solución o demostración.
Tuvo gran variedad de disputas y alianzas con distintos matemáticos de la época, quienes amaban u odiaban trabajar con él.
Su último teorema fue el principal responsable de su fama mundial, donde afirmó que una generalización del teorema de Pitágoras para cualquier grado “n”, era imposible. Dijo poseer una demostración valida de ello, pero murió antes de hacerla pública.
Dicha demostración tuvo que esperar 350 años aproximadamente. En 1995 los matemáticos Andrew Wiles y Richard Taylor, pusieron fin a la zozobra dejada por Fermat, demostrando que tenía razón a través de una demostración válida de su último teorema.
Defina la pendiente de la recta tangente a la curva f(x)=x2 en el punto (4 , 16)
Sustituyendo en la expresión del límite de Fermat se tiene:
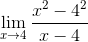
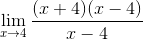
Se simplifican los factores ( x – 4 )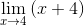
Al evaluar se tiene
M = 4 + 4 = 8
Defina el punto crítico de la expresión f(x) = x2 + 4x usando el límite de Fermat

Se realiza una agrupación estratégica de elementos, buscando agrupar los pares X-X0

Se desarrollan los mínimos cuadrados
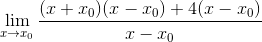
Se observa el factor común X-X0 y se extrae
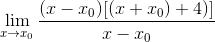
Ya puede simplificarse la expresión y romperse la indeterminación
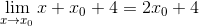
En los puntos mínimos se sabe que la pendiente de la recta tangente es igual a cero. De tal modo podemos igualar a cero la expresión encontrada y despejar el valor X0
2 X0 + 4 = 0
X0 = -4/2 = -2
Para conseguir la coordenada faltante solo hace falta evaluar el punto en la función original
F(-2) = (-2)2 + 4(-2) = 4 – 8 = – 4
El punto crítico es P ( -2 , -4 ).
- Real Analysis. A Historical Approach Sauhl Stahl, John Wiley & Sons, 5 ago. 1999.
- The Mathematical Career of Pierre de Fermat, 1601-1665: Second Edition. Michael Sean Mahoney. Princeton University Press, 5 jun. 2018
- From Fermat to Minkowski: Lectures on the Theory of Numbers and Its Historical Development. W. Scharlau, H. Opolka, Springer Science & Business Media, 1985
- Fermat’s Last Theorem: A Genetic Introduction to Algebraic Number Theory. Harold M. Edwards. Springer Science & Business Media, 14 ene. 2000
- Fermat Days 85: Mathematics for Optimization. J.-B. Hiriart-Urruty Elsevier, 1 ene. 1986
