Ohm: medidas de resistencias, ejemplos y ejercicio resuelto

El ohm u ohmio es la unidad de medida de la resistencia eléctrica perteneciente al Sistema Internacional de Unidades (SI), ampliamente utilizado en ciencia e ingeniería. Se nombró así en honor al físico alemán Georg Simon Ohm (1789-1854).

Ohm fue profesor e investigador en la Universidad de Múnich, y entre sus muchos aportes a la electricidad y el magnetismo se cuenta la definición de la resistencia a través de la relación existente entre el voltaje y la corriente que atraviesa un conductor. 

A esta relación se la conoce como la Ley de Ohm y suele expresarse como: 

R = ΔV/I

Donde R representa la resistencia eléctrica, ΔV es el voltaje en voltios (V) e I es la corriente en amperios (A), todo en unidades SI.

Por lo tanto, 1 ohm, que también se denota indistintamente con la letra griega Ω, equivale a 1 V/A. Significa que si establecer un voltaje de 1 V a través de cierto conductor origina una corriente de 1 A, la resistencia de dicho conductor es de 1 Ω.

La resistencia eléctrica es un elemento de circuito muy común que se utiliza de muchas formas para controlar adecuadamente la corriente, tanto si forma parte de un circuito integrado o de manera individual.

Índice del artículo

• 1 Medida de la resistencia eléctrica
  • 1.1 Código de colores para las resistencias
• 2 Ejemplos de valores de resistencias
  • 2.1 Prefijos más utilizados
  • 2.2 Resistencia de un conductor
• 3 Ejercicio resuelto
• 4 Referencias

Medida de la resistencia eléctrica

Las resistencias se miden con la ayuda de un multímetro, un medidor que viene en versiones analógicas y digitales. Los más básicos miden voltajes y corrientes directos, pero existen aparatos más sofisticados con funciones adicionales. Cuando se usan para medir resistencia se denominan óhmetros u ohmimetros. Este aparato es muy sencillo de usar:

– Se coloca el selector central en la posición para medir resistencia, escogiendo una de las escalas identificadas con el símbolo Ω, en caso de que el instrumento disponga de más de una.

– La resistencia a medir se extrae del circuito. Si no es posible, es preciso apagar la fuente de alimentación.

– Se coloca la resistencia entre las puntas o sondas del instrumento. La polaridad no importa.

– El valor se lee directamente en la pantalla digital. Si el instrumento es analógico, tiene una escala marcada con el símbolo Ω que se lee de derecha a izquierda.

En la siguiente figura (número 2), se muestra un multímetro digital y sus sondas o puntas. El modelo tiene una sola escala para medir resistencias, señalada con una flecha.

Frecuentemente el valor de una resistencia eléctrica comercial viene expresado por un código de bandas de colores en su exterior. Por ejemplo, las resistencias de la figura 1 tienen bandas rojas, violetas, doradas, amarillas y grises. Cada color tiene un significado numérico que indica el valor nominal, como se mostrará seguidamente.

Código de colores para las resistencias

En la siguiente tabla aparecen los códigos de colores para las resistencias:

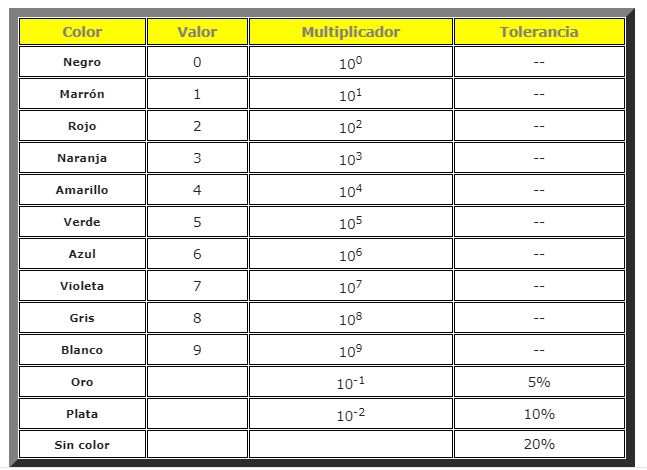
Tomando en cuenta que la banda metalizada queda a la derecha, el código se utiliza de la siguiente manera:

– Los dos primeros colores de izquierda a derecha dan el valor de la resistencia.

– El tercer color señala la potencia de 10 por la cual se debe multiplicar.

– Y el cuarto indica la tolerancia establecida por el fabricante.

Ejemplos de valores de resistencias

A modo de ejemplo veamos primero la resistencia en primer plano, a la izquierda de la figura 1. La secuencia de colores mostrada es: gris, rojo, rojo, dorado. Hay que recordar que la banda oro o plata debe estar a la derecha.

El gris representa 8, el rojo es 2, el multiplicador es rojo e igual a 10² = 100 y finalmente, la tolerancia es dorada que simboliza 5%. Por lo tanto la resistencia vale 82 x 100 Ω = 8200 Ω.

Siendo la tolerancia de 5 %, la misma equivale en ohmios a: 8200 x (5/100) Ω = 410 Ω. Por lo tanto el valor de la resistencia está comprendido entre: 8200 – 410 Ω = 7790 Ω y 8200 + 410 Ω = 8610 Ω.

Mediante el código de colores se tiene el valor nominal o de fábrica de la resistencia, pero para precisar la medida, se necesita medir la resistencia con el multímetro, según se explicó antes.

Otro ejemplo para la resistencia de la siguiente figura:

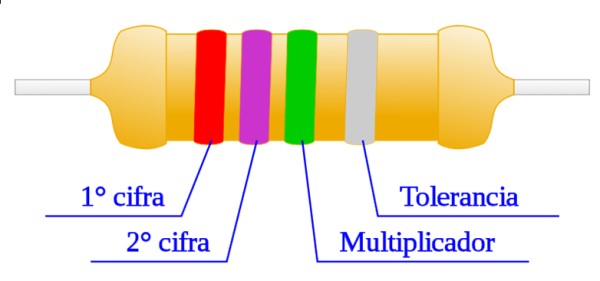
Tenemos lo siguiente para la resistencia R: rojo (=2), violeta (= 7), verde (multiplicar por 10⁵), por lo que la resistencia R de la figura vale 27 x 10⁵ Ω. La banda de la tolerancia es plateada: 27 x 10⁵ x (10/100) Ω = 27 x 10⁴ Ω. Una forma de expresar el resultado anterior, redondeando 27 x 10⁴ a 30 x 10⁴, es:

R = (27 ± 3) × 10⁵ Ω = (2.7 ± 0.3) × 10⁶ Ω 

Prefijos más utilizados

Los valores que puede tener una resistencia eléctrica, que siempre es positiva, están en un rango muy amplio. Por ello se utilizan mucho las potencias de 10 para expresar sus valores, así como los prefijos. A continuación los más usuales:

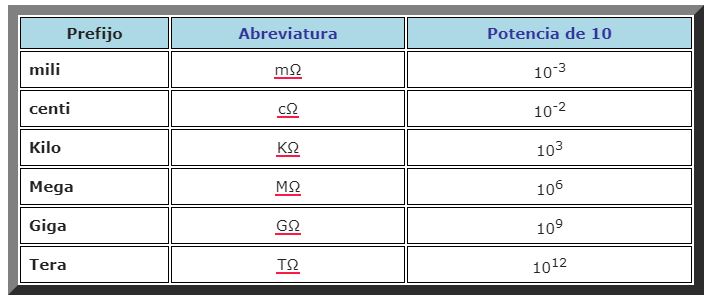
Según esta notación, la resistencia del ejemplo anterior es: (2.7 ± 0.3) MΩ.

Resistencia de un conductor

Las resistencias se fabrican de diversos materiales y es una medida de la oposición que tiene el conductor al paso de la corriente, como es sabido, no todos los materiales conducen de igual forma. Incluso entre los materiales considerados como conductores hay diferencias.

La resistencia depende de varias características, siendo las más importantes:

– Geometría del conductor: longitud y área de la sección transversal.

– Resistividad del material: indica la oposición que presenta el material al paso de la corriente.

– Temperatura: la resistividad y la resistencia aumentan con la temperatura, ya que el ordenamiento interno del material disminuye y así los portadores de corriente ven obstaculizado su paso.

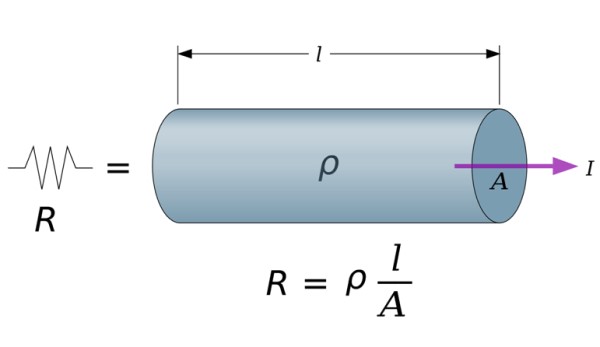
Para un conductor de sección transversal constante, a una temperatura dada la resistencia viene dada por:

R = ρ (ℓ/A)

Donde ρ es la resistividad del material a la temperatura en cuestión, la cual se determina experimentalmente, ℓ es la longitud del conductor y A es el área de sección transversal.

Ejercicio resuelto

Hallar la resistencia de un alambre de cobre de 0.32 mm de radio y 15 cm de longitud, sabiendo que la resistividad del cobre es 1.7 × 10^-8 Ω.m.

Solución

Dado que la resistividad está en unidades del Sistema Internacional, lo más adecuado es expresar el área de sección transversal y la longitud en dichas unidades, para después sustituir en la fórmula de la sección precedente:

Radio = 0.32 mm = 0.32 ×10^-3 m

A = π (Radio²) = π (0.32 × 10^-3 m)² = 3.22 x 10^-7 m²

ℓ = 15 cm = 15 x 10^-2 m

R = ρ (ℓ/A) = 1.7 × 10^-8 Ω.m x (15 x 10^-2 m / 3.22 x 10^-7 m² ) = 7.9 ×10^-3 Ω = 7.9 m-ohm.

Referencias

1. Figueroa, D. (2005). Serie: Física para Ciencias e Ingeniería. Volumen 5. Electrostática. Editado por Douglas Figueroa (USB).
2. Giancoli, D.  2006. Physics: Principles with Applications. 6^th. Ed Prentice Hall.
3. Resnick, R. (1999). Física. Vol. 2. 3^ra en español. Compañía Editorial Continental S.A. de C.V.
4. Sears, Zemansky. 2016. University Physics with Modern Physics. 14^th. Ed. Volume 2.
5. Serway, R., Jewett, J. (2018). Física para Ciencias e Ingeniería. Volumen 1. 10^ma. Ed. Cengage Learning.