Teorema del binomio: concepto, demostración y ejemplos

¿Qué es el teorema del binomio?
El teorema del binomio es una ecuación que nos dice cómo se desarrolla una expresión de la forma (a+b)n para algún número natural n. Un binomio no es más que la suma de dos elementos, como (a+b). También nos permite saber para un término dado por akbn-k cuál es el coeficiente que lo acompaña.
Este teorema es comúnmente atribuido al inventor, físico y matemático inglés sir Isaac Newton; sin embargo, se han encontrado diversos registros que indican que en el Medio Oriente ya se conocía su existencia, alrededor del año 1000.
Números combinatorios
El teorema del binomio nos dice matemáticamente lo siguiente:
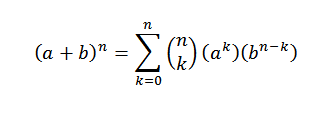
En esta expresión a y b son números reales y n es un número natural.
Antes de dar la demostración, veamos algunos conceptos básicos que son necesarios.
El número combinatorio o combinaciones de n en k es expresado de la siguiente manera:
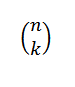
Esta forma expresa el valor de cuántos subconjuntos con k elementos se pueden elegir de un conjunto de n elementos. Su expresión algebraica viene dada por:
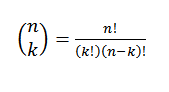
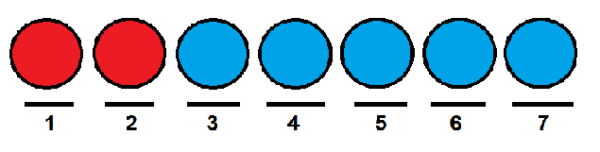
Veamos un ejemplo: supongamos que tenemos un grupo de siete pelotas, de las cuales dos de son rojas y el resto son de color azul.
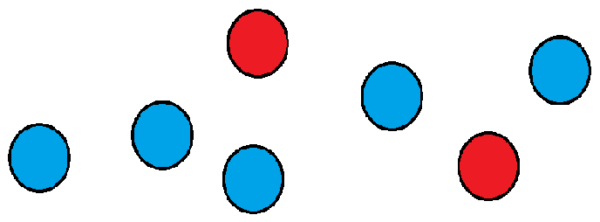
Queremos saber de cuántas maneras podemos ordenarlas en fila. Una manera podría ser colocar las dos rojas en la primera y segunda posición, y el resto de las pelotas en las posiciones que quedan.
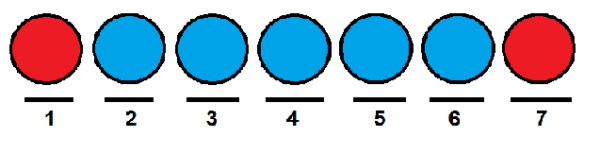
Similar al caso anterior, podríamos darles a las pelotas rojas la primera y la última posición respectivamente, y ocupar las otras con pelotas azules.
Ahora, una forma eficaz de contar de cuántas maneras podemos ordenar las pelotas en fila es usando a los números combinatorios. Podemos ver a cada posición como un elemento del siguiente conjunto:
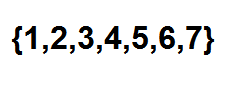
A continuación solo queda elegir un subconjunto de dos elementos, en el cual cada uno de estos elementos representa la posición que ocuparán las pelotas rojas. Esta elección la podemos hacer según la relación dada por:
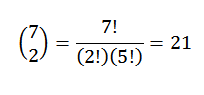
De esta manera, tenemos que existen 21 maneras de ordenar dichas pelotas.
La idea general de este ejemplo nos será de gran utilidad en la demostración del teorema del binomio. Observemos un caso particular: si n = 4, tenemos (a+b)4, que no es más que:
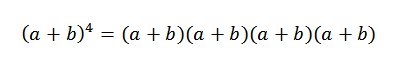
Cuando desarrollamos este producto, nos queda la suma de los términos que se obtienen al multiplicar un elemento de cada uno de los cuatro factores (a+b). Así, tendremos términos que serán de la forma:
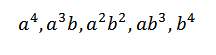
Si quisiéramos obtener el término de la forma a4, solo basta con multiplicar de la siguiente manera:
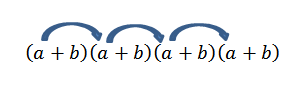
Nótese que solo hay una forma de obtener este elemento; pero, ¿qué pasa si ahora buscamos el término de la forma a2b2? Como “a” y “b” son números reales y, por lo tanto, vale la ley conmutativa, tenemos que una forma de obtener este término es multiplicar con los miembros como indican las flechas.
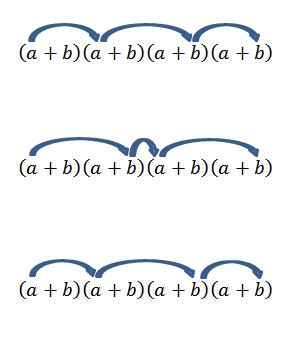
Realizar todas estas operaciones suele ser algo tedioso, pero si vemos el término “a” como una combinación en donde deseamos saber de cuántas maneras podemos elegir dos “a” de un conjunto de cuatro factores, podemos usar la idea del ejemplo anterior. Entonces, tenemos lo siguiente:
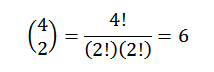
Así pues, sabemos que en el desarrollo final de la expresión (a+b)4 tendremos exactamente 6a2b2. Usando la misma idea para los demás elementos, se tiene que:
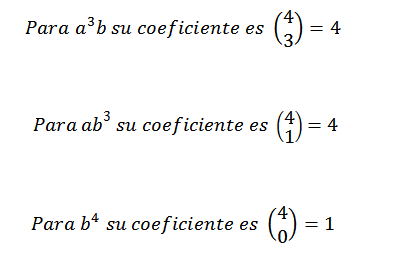
Luego sumamos las expresiones obtenidas anteriormente y nos queda que:
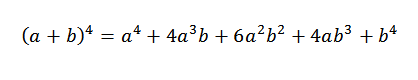
Se trata de una demostración formal para el caso general en el que “n” sea cualquier número natural.
Demostración
Notemos que los términos que quedan al desarrollar (a+b)n son de la forma akbn-k, donde k=0,1,…,n. Usando la idea del ejemplo anterior, tenemos la forma de elegir “k” variables “a” de los “n” factores es de:
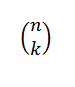
Al elegir de esta manera, automáticamente estamos eligiendo n-k variables “b”. De esto se sigue que:
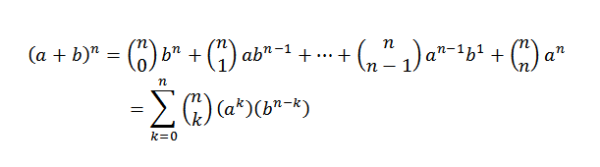
Ejemplos
Considerando (a+b)5, ¿cuál sería su desarrollo?
Por el teorema del binomio tenemos que:
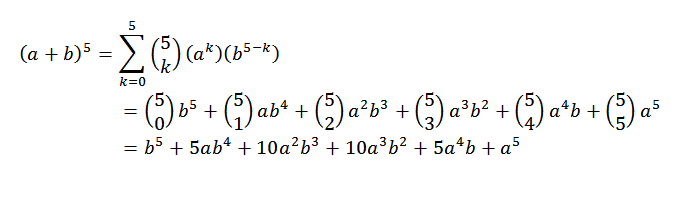
El teorema del binomio nos resulta muy útil si tenemos una expresión en la que queremos saber cuál es el coeficiente de un término en específico sin tener que realizar el desarrollo completo. Como ejemplo podemos tomar la siguiente incógnita: ¿cuál es el coeficiente de x7y9 en el desarrollo de (x + y)16?
Por el teorema del binomio, tenemos que el coeficiente es:
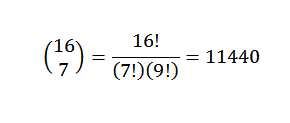
Otro ejemplo sería: ¿cuál es el coeficiente de x5y8 en el desarrollo de (3x-7y)13?
Primero rescribimos la expresión de una manera conveniente; esto es:
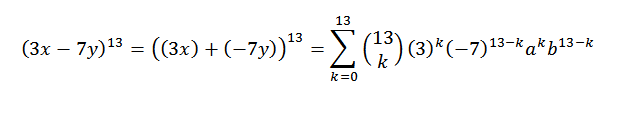
Luego, usando el teorema del binomio, tenemos que el coeficiente buscado es cuando se tiene k = 5
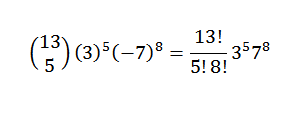
Otro ejemplo de los usos de este teorema es en la demostración de algunas identidades comunes, como las que mencionaremos a continuación.
Identidad 1
Si “n” es un número natural, tenemos que:
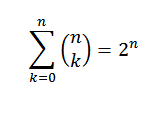
Para la demostración usamos el teorema del binomio, donde tanto “a” como “b” toman el valor de 1. Entonces nos queda:
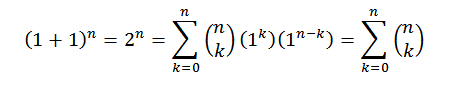
De esta forma tenemos probada la primera identidad.
Identidad 2
Si “n” es un número natural, entonces
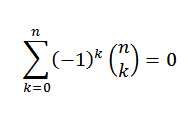
Por el teorema del binomio tenemos que:
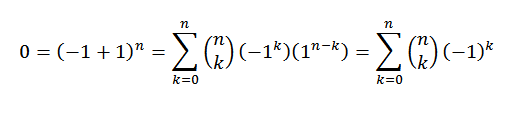
Otra demostración
Podemos hacer una demostración distinta para el teorema de binomio haciendo uso del método inductivo y la identidad de pascal, la cual nos dice que, si “n” y “k” son enteros positivos que cumplen con n ≥ k, entonces:
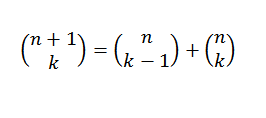
Demostración por inducción
Primero veamos que la base inductiva se cumple. Si n = 1, tenemos que:
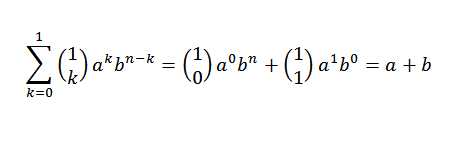
Efectivamente, vemos que se cumple. Ahora, sea n = j tal que se cumple:
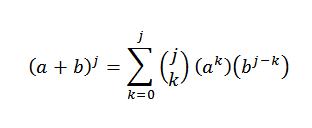
Queremos ver que para n= j+1 se cumple que:
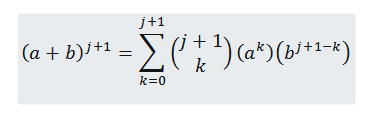
Entonces, tenemos que:
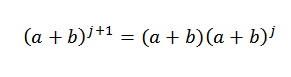
Por hipótesis sabemos que:
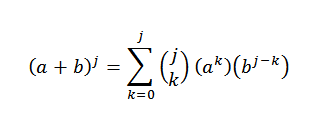
Luego, usando la propiedad distributiva:
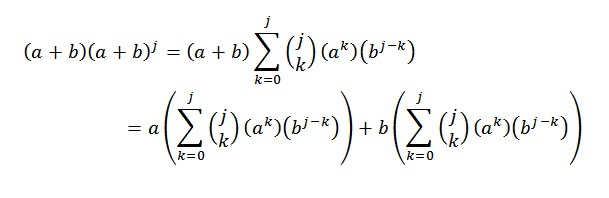
Posteriormente, desarrollando cada una de las sumatorias se tiene:
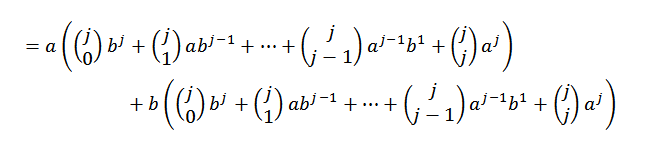
Ahora, si agrupamos de manera conveniente, nos queda que:
Usando la identidad de pascal, tenemos que:
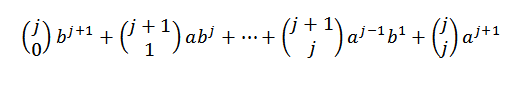
Para finalizar, nótese que:
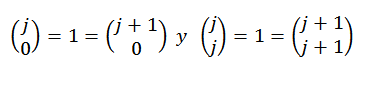
Por lo tanto, vemos que el teorema del binomio se cumple para todo “n” perteneciente a los números naturales, y con esto termina la prueba.
Curiosidades
El número combinatorio (nk) también es llamado coeficiente binomial por ser precisamente el coeficiente que aparece en el desarrollo del binomio (a+b)n.
Isaac Newton dio una generalización de este teorema para el caso en el cual el exponente es un número real; este teorema es conocido como el teorema del binomio de Newton.
Ya en la antigüedad se conocía este resultado para el caso particular en el que n=2. Este caso es mencionado en los Elementos de Euclides.
