Cultura general
2021-08-21T15:42:38+02:00

Distribución exponencial: qué es, características, fórmulas, ejemplos

¿Qué es la distribución exponencial?

La distribución exponencial es un modelo probabilístico para variables aleatorias continuas. Esto significa que, a través de él, se puede conocer la probabilidad de ocurrencia de un determinado valor de la variable, por lo que es una distribución de probabilidad.

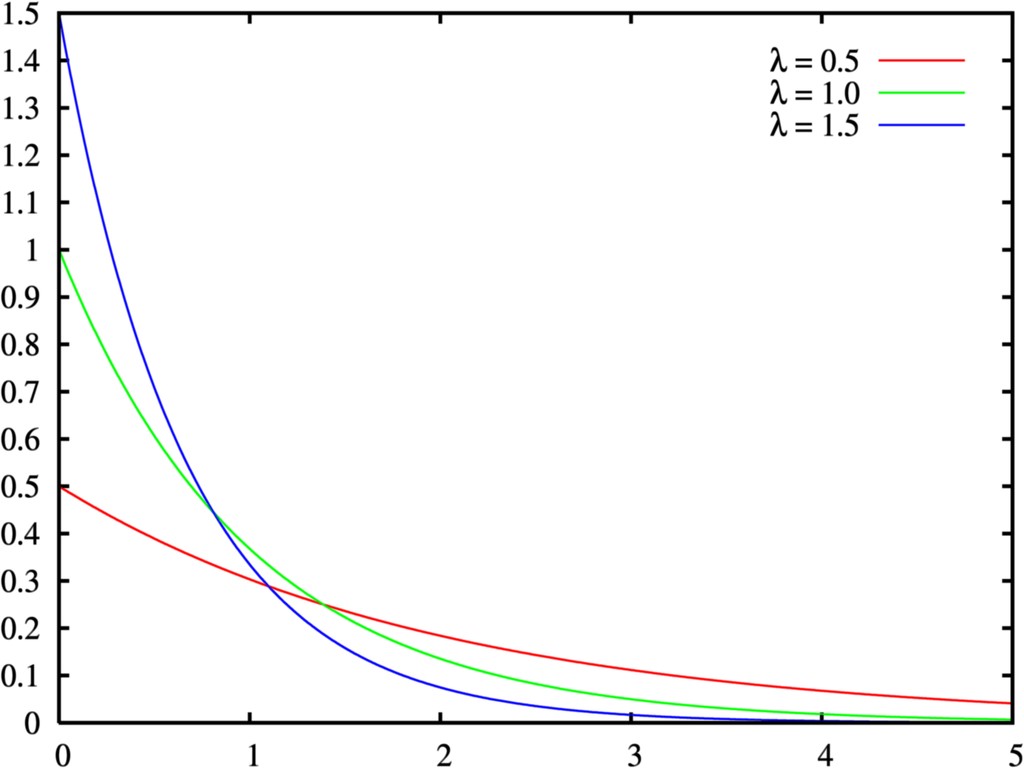
Para obtener la distribución, se parte de una función de densidad, la cual tiene forma exponencial de parámetro λ > 0:

0 // 0& /text{ si } x/leq 0 /end{cases}" src="https://latex.codecogs.com/gif.latex?f(x)=%5Cbegin%7Bcases%7D&space;%5Clambda&space;e%5E%7B-%5Clambda&space;x%7D&&space;%5Ctext%7B&space;si&space;%7D&space;x>0&space;%5C%5C&space;0&&space;%5Ctext%7B&space;si&space;%7D&space;x%5Cleq&space;0&space;%5Cend%7Bcases%7D" width="178" height="48">

La función de densidad como tal no permite calcular la probabilidad, pero una vez establecida f(x), la función de distribución F(x), mediante la cual se obtienen las probabilidades, se obtiene mediante integración de f(x). Por ejemplo, la probabilidad P de que la variable aleatoria tome valores comprendidos entre 0 y x es:

Llevando a cabo la integración, que es muy sencilla, pues la integral de una exponencial es la misma exponencial, salvo por las constantes que acompañan al argumento, se obtiene:

La distribución exponencial se utiliza mucho para determinar la probabilidad de que ocurra un evento tras un determinado tiempo de espera, como por ejemplo el tiempo que transcurre en la emergencia de un hospital antes de que llegue un paciente.

Con frecuencia, los eventos se refieren a la falla o avería de componentes eléctricos, electrónicos y de otros tipos. En tal caso, la distribución exponencial ayuda a estimar el tiempo que tarda un componente en fallar, y también el tiempo transcurrido entre reparaciones. A esto se le conoce como teoría de la fiabilidad.

Características de la distribución exponencial

Algunas de las características más destacadas de la función de densidad f(x) de la distribución exponencial son las siguientes:

f(x) es positiva.
El área bajo la curva y = f(x)= λe^−λ^x siempre es igual a 1, porque que la suma de las probabilidades de ocurrencia de todos los valores de la variable tiene que ser 1. Esta es una condición que cumplen las funciones de densidad. Dicha área se calcula a través de la integral:

Falta de memoria de la distribución exponencial

La característica más destacada de la distribución exponencial es su carencia de memoria. Por ejemplo, supóngase que se está modelando con esta distribución el tiempo transcurrido hasta que ocurre la falla de un elemento.

Pues bien, la falta de memoria se refiere a que saber que el elemento funcionó un tiempo de supervivencia “s”, no modifica la probabilidad de que el elemento siga funcionando hasta una cierta cantidad de tiempo adicional “t”.

Es decir, que la probabilidad de que el elemento falle de aquí a un cierto tiempo (1 minuto, 1 hora, por ejemplo) no depende de que haya funcionado bien hasta el momento.

Matemáticamente se calcula mediante definición de probabilidad de sucesos independientes:

Por lo tanto, la probabilidad no depende de s o tiempo de supervivencia.

Fórmulas

1.- La función de densidad de la distribución exponencial es:

Donde λ es el parámetro de la distribución.

2.- Tal como se describió anteriormente, la distribución de probabilidades propiamente dicha se denota como F(x) y las distintas probabilidades se obtienen por integración de la función de densidad:

0 /end{cases}" src="https://latex.codecogs.com/gif.latex?F(x)=%5Cbegin%7Bcases%7D&space;0&space;&&space;%5Ctext%7B&space;si&space;%7D&space;x%5Cleq&space;0&space;%5C%5C&space;1-e%5E%7B-%5Clambda&space;x%7D&&space;%5Ctext%7B&space;si&space;%7D&space;x>0&space;%5Cend%7Bcases%7D" class="">

3.- De lo anterior se desprende que la probabilidad de que la variable tome valores menores o iguales a “x” es P[X≤x] = 1 −e^−λ^x.

4.- El área bajo la curva y = f(x), comprendida entre a y b permite calcular la probabilidad de que la variable se encuentre en el intervalo [a, b]. Dicha área es:

P [a ≤ x ≤ b] = F (b) – F (a)

5.- El valor de P [x ≥ a] es 1 – F(a) = 1 – (1 − e^−λ^x) = e^−λ^x

Valor esperado de la distribución exponencial

La esperanza o valor esperado E(x) de la distribución exponencial es el valor que se espera ocurra con mayor frecuencia. Se calcula a partir de la integral:

E(x) = 1/λ

Varianza de la distribución exponencial

Para el cálculo de la varianza hay que determinar la integral:

La cual también se resuelve con el método de integración por partes, para obtener:

Var (x) = 1/λ²

Una particularidad de la distribución exponencial es que la desviación estándar S(x), definida como la raíz cuadrada de la varianza es:

S(x) = √Var(x) =√(1/λ²) = 1/λ

Es decir, la desviación estándar es igual a la esperanza de la distribución.

Ejemplos de distribución exponencial

Datación de muestras por carbono 14

La distribución exponencial se usa para determinar el tiempo que tarda en desintegrarse una partícula radiactiva. Estos tiempos se utilizan para datar muestras fósiles mediante radiocarbono.

Tiempo que se tarda en revisar el correo

Se puede modelar el tiempo que tardan los usuarios en revisar su correo electrónico, una vez recibida la notificación, mediante una distribución exponencial. Supóngase que el parámetro de la distribución es λ = 0.2, entonces, la probabilidad de que una persona demore menos de 1 minuto en revisar su correo es:

Esta integral se resolvió al comienzo, solo queda sustituir los valores numéricos en la solución y calcular el resultado final:

P[x ≤ 1]=1−e⁻^0.2^×¹ = 1− e⁻^0.2 = 1− 0.819 = 0.181

También se puede sustituir directamente en la función F(x) dada anteriormente, para obtener F(1).

Ejercicios

Ejercicio 1

Hallar la probabilidad de que una persona tarde más de una hora revisando su correo, si la distribución de probabilidades es exponencial, con parámetro λ = 0.2.

Solución

Se debe calcular P [x ≥ 60], puesto que 1 hora equivale a 60 minutos y se pide la probabilidad de que la persona tarde 60 minutos o más en revisar el correo. La probabilidad se calcula con la misma integral presentada al comienzo, solo cambiando los límites de integración:

El valor obtenido es pequeño, por lo que es muy poco probable que una persona se demore más de una hora en revisar su correo electrónico.

Ejercicio 2

Las bombillas eléctricas suelen tener una duración finita, excepto la famosa bombilla de la estación de bomberos en Livermore, California, que nunca ha fallado desde que fuera encendida por primera vez, en 1901.

Supóngase que la duración de una bombilla actual sigue una distribución exponencial, con un valor esperado de 8 meses. Calcular:

a) ¿Cuál es la probabilidad de que la bombilla dure entre 5 y 14 meses?

b) La probabilidad de que la bombilla dure más de 25 meses, sabiendo que tiene más de 11 meses en funcionamiento.

Solución a

Lo primero es encontrar el valor de λ, a través del valor esperado de la distribución E(x) = 8 meses. De acuerdo a lo dicho en la sección precedente, el valor esperado es el inverso del parámetro λ, por lo tanto:

E(x) = 1/λ → λ = 1 /E(x) = 1 / 8 = 0.125

Seguidamente se calcula la probabilidad pedida, mediante la integral dada al comienzo, pero cambiando convenientemente los límites de integración:

Seguidamente se sustituye en la función F(x) dada en la sección precedente, de la siguiente manera:

P [5 ≤ X ≤ 14] = F (14) – F (5) = [1 – e^-(0.125×14)] − [1 – e^-(0.125×5)] = 0.36

Solución b

Para responder esta cuestión se usará la propiedad de la falta de memoria, enunciada más arriba. Como se sabe que ha durado ya más de 11 meses, entonces:

s = 11 meses

El tiempo adicional para que dure 25 meses o más es:

t = 14 meses

P [x ≥ s + t│t ≥ s] = P [x ≥ 11+14│t ≥ 11] = e^−0.125×14= 0.174