Homotecia negativa: como se hace, ejemplos y ejercicios

¿Qué es la homotecia negativa?

La homotecia negativa es una transformación en la que un polígono contenido en un plano tiene como imagen otro polígono en ese mismo plano, de iguales ángulos y con los lados correspondientes proporcionales a los del original. Cuando la homotecia es negativa la imagen queda rotada media vuelta respecto a la figura inicial.

La homotecia se caracteriza por tener un centro de homotecia O y una constante de proporcionalidad llamada la razón r. Cuando r es un número negativo entonces se habla de homotecia negativa.

¿Cómo se hace una transformación de homotecia?

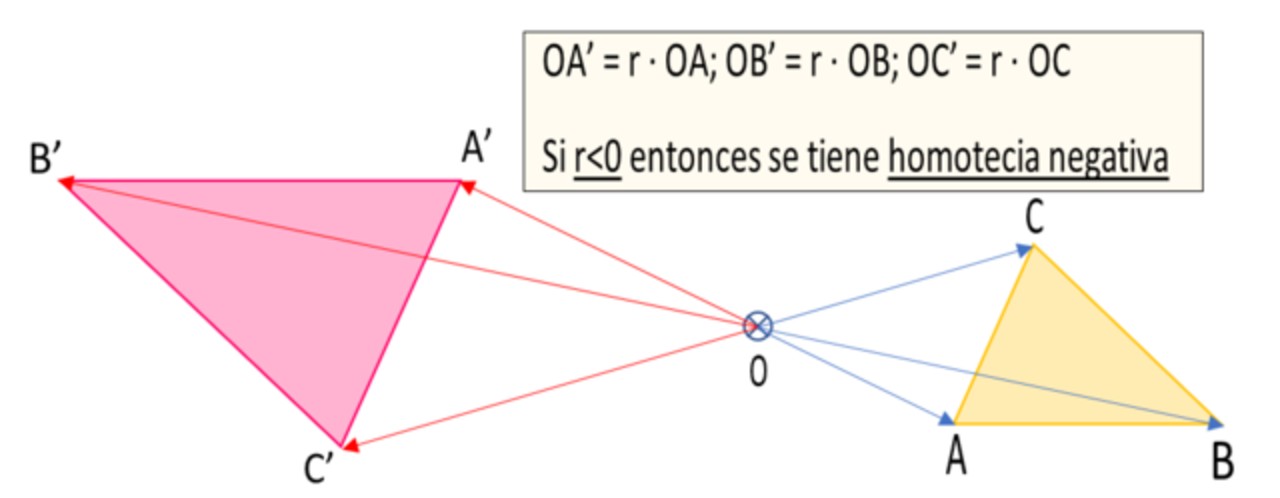
Para explicar como se realiza una homotecia negativa tomaremos el caso de la figura 1 en la que se tiene un triángulo ABC al que se le quiere construir su homotético negativo.

1.- Se parte por elegir un centro de homotecia, que es este caso es el punto O.

2.- A partir de O se construyen los segmentos orientados (vectores) OA, OB y OC que van del centro de homotecia a cada uno de los vértices del triángulo.

3.- Se elige una razón de homotecia r. Como se quiere una homotecia negativa, entonces r debe ser menor que cero. En el caso de la figura 1 se tomó r= -1.5.

4.- Se trazan los vectores OA’, OB’ y OC’, los cuales son respectivamente OA’ = r ∙ OA, OB’ = r ∙ OB  y OC’ = r ∙ OC. Como r = -1.5, es decir un número negativo, entonces los vectores OA’, OB’ y OC’ tienen dirección contraria a sus homólogos correspondientes, es decir OA, OB y OC. Pero como el valor absoluto de la razón r es |r|= 1.5 los tamaños de OA’, OB’ y OC’ son una vez y media mayor que la de sus homólogos OA, OB y OC.

5.- Las puntas de los vectores OA’, OB’ y OC’ definen los vértices del triángulo A’B’C’ que es el homotético negativo del triángulo ABC.

Propiedades de la homotecia negativa

La homotecia negativa, también denominada homotecia inversa, tiene las siguientes propiedades:

1.- Los lados correspondientes entre el polígono imagen y el polígono original tienen longitudes proporcionales, siendo la constante de proporcionalidad el valor absoluto de la razón de homotecia, es decir la imagen está amplificada en un factor |r| siempre que |r| sea mayor que la unidad, pero la imagen se reduce si |r| es menor que la unidad.

2.- Los ángulos entre lados correspondientes de la figura imagen y de la figura original tienen las mismas medidas.

3.- Los lados homólogos entre original e imagen son paralelos entre sí.

4.- Los segmentos correspondientes en el caso de homotecia negativa son paralelos, pero con orientación o sentido contrario. Por ejemplo en la figura 1, el segmento AB tiene su homologo A’B’ paralelo al primero, pero con dirección opuesta.

Comparación con la homotecia positiva

Se llama homotecia positiva aquella en la que la razón de homotecia es un número positivo. Para construir una homotecia positiva se siguen los mismos pasos que los de la homotecia negativa:

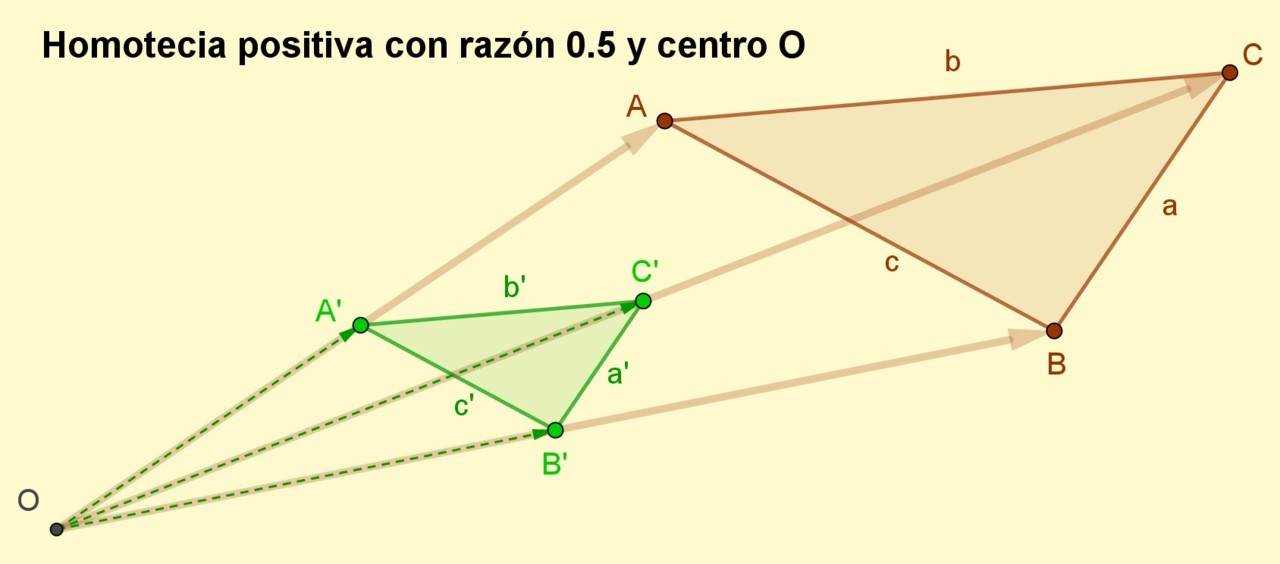
1.- Elegir un centro de homotecia, en nuestro caso el punto O (ver figura 2).

2.- Trazar los segmentos orientados (vectores), que van del centro de homotecia hasta los vértices del polígono, en el caso de la figura 2 estos son: OA, OB y OC.

3.- Elegir una razón de homotecia que sea un número positivo, por ejemplo, en el caso de la figura 2 se ha elegido r= 0.5.

4.- Se trazan los vectores OA’, OB’ y OC’, los cuales son respectivamente OA’ = r ∙ OA, OB’ = r ∙ OB y OC’ = r ∙ OC. Como r es un número positivo, entonces los vectores OA’, OB’ y OC’ tienen la misma dirección que OA, OB y OC. Las longitudes de OA’, OB’ y OC’ son la mitad que la de sus homólogos OA, OB y OC, ya que la razón es r= 0.5.

5.- Finalmente se unen los vértices A’B’C’ para obtener el triángulo homotético a ABC con razón 1/2.

Ejemplos de homotecia

La homotecia aparece en diversas situaciones:

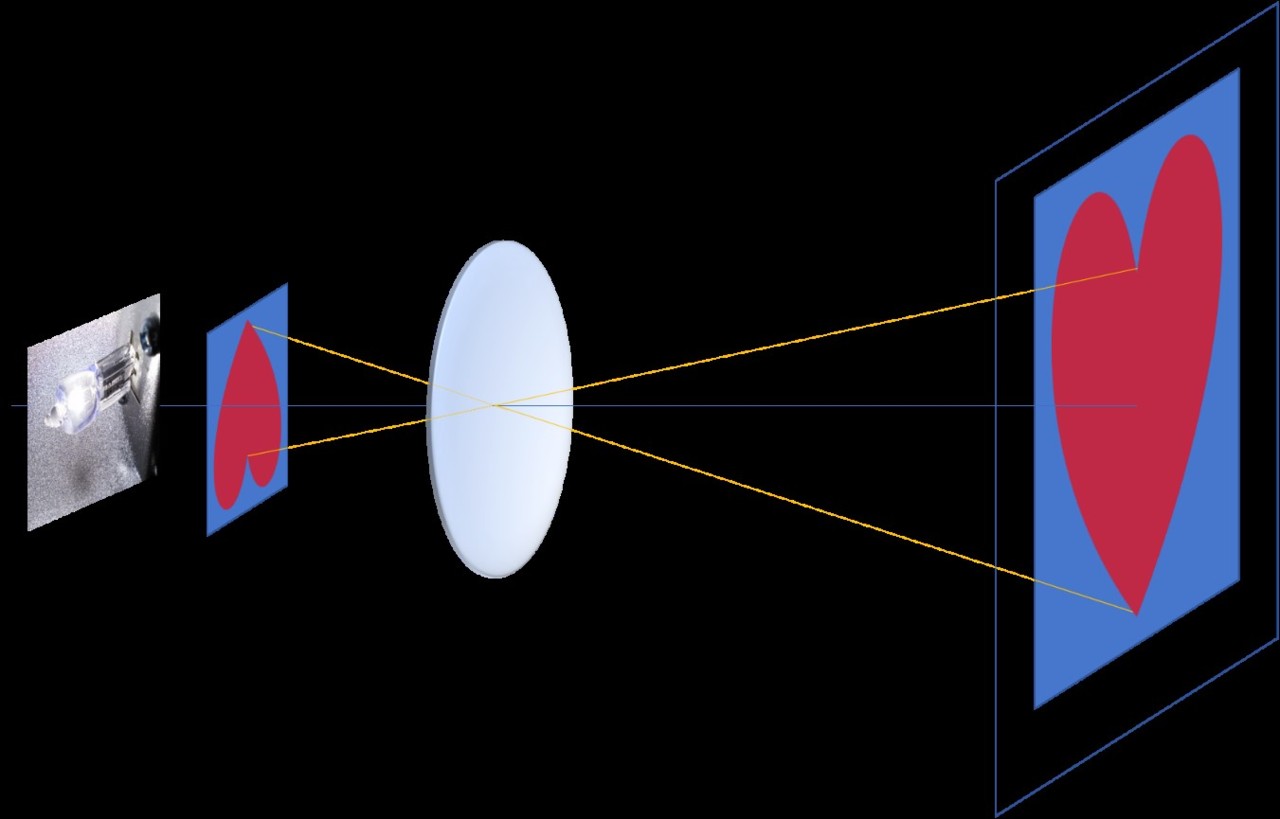
Proyectores de cine

En un proyector de cine la imagen grabada en un fotograma se proyecta y amplía sobre una pantalla, y para que la proyección se vea al derecho es necesario que el fotograma esté invertido, ya que el centro de homotecia está en el centro de la lente del proyector, entre el fotograma y la pantalla (homotecia negativa, ver figura 3)

Cámaras fotográficas

Este principio también aplica a las cámaras fotográficas: la luz proveniente de la imagen ubicada a cierta distancia de la lente se proyecta sobre el sensor fotográfico, el cual puede ser una película química sensible a la luz o un sensor CCD, si se trata de una cámara digital.

La imagen registrada en el sensor está invertida respecto a la real y suele ser proporcionalmente menor que ella.

Aplicación práctica

El Sol no se debe mirar directamente, pues causa daño permanente en la retina, pero hay dos posibilidades para estudiarlo: usar filtros que atenúen la intensidad luminosa o proyectar su imagen sobre una pantalla.

Un dispositivo de proyección consiste en un tubo de longitud d. Uno de los extremos del tubo se tapa con papel de aluminio y se perfora en su centro con un alfiler. El otro extremo, que servirá de pantalla, se tapa con papel translúcido, el cual puede ser papel cebolla o papel albanene (papel vegetal).

Ejercicio

Determinar el diámetro del Sol, sabiendo que el radio orbital terrestre es del orden de 150 millones de kilómetros, que el tubo de proyección, como el mostrado en la figura 4, tiene 2,2 metros de longitud y que la imagen proyectada es de 2,1 cm de diámetro.

Solución

Los datos son los siguientes:

• Longitud del tubo: d = 2,2m
• Diámetro de la imagen proyectada del Sol: s = 2,1 cm
• Distancia del tubo al Sol: R = 150 x 10^9 m
• Diámetro real del Sol: S = ¿?

Para obtener el diámetro del Sol se aplica una relación de proporcionalidad según la proporcionalidad de la homotecia (ver figura 4):

La distancia al Sol es a la longitud del tubo como el diámetro del Sol es al diámetro de la imagen proyectada:

(R / d) = (S / s)

Despejando de esta igualdad se tiene que el diámetro real del Sol es el diámetro de la proyección multiplicado por el cociente entre la distancia al Sol y la longitud del tubo:

S = s (R / d)

Colocando los valores numéricos se tiene:

S = 2,1 x 10^-2 m (150 x 10⁹ m / 2,2 m)

S = 1,43 x 10⁹ m.

Este resultado se interpreta así: el diámetro real del Sol es 1,43 millones de kilómetros.

Referencias

1. Álvaro Rendón, A. R. 2004. Dibujo Técnico: cuaderno de actividades.
2. Antonio Álvarez de la Rosa, J. L. 2002. Afinidad, Homología y Homotecia.
3. Baer, R. 2012. Linear Algebra and Projective Geometry. Courier Corporation.
4. Hebert, Y. 1980. Matemáticas generales, probabilidades y estadística.
5. Meserve, B. E. 2014. Fundamental Concepts of Geometry. Courier Corporation