Radio de convergencia: definición, ejemplos y ejercicios resueltos
El radio de convergencia de una serie de potencias es el radio del círculo de convergencia al cual la serie converge. Dicho círculo se extiende desde el valor que anula la base de las potencias hasta la singularidad más cercana de la función asociada a la serie.
Toda función analítica f(z) tiene asociada una serie de potencias en torno un punto no singular, denominada serie de Taylor:
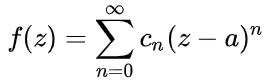
Donde a es el centro del círculo de convergencia, z la variable independiente de la función y los cn son coeficientes relacionados con las derivadas de la función f en el punto z=a.
El radio de convergencia r es un número real positivo que define la región:
|z – a| r
Donde la serie converge. Fuera de esa región la serie diverge, es decir toma valores infinitos. Cuando el radio de convergencia es infinito, entonces la serie converge en todo el plano complejo.
Índice del artículo
Para que una serie sea convergente es necesario que el valor absoluto de los términos sucesivos vaya en disminución cuando el número de términos sea muy grande. En forma matemática se expresaría de la siguiente manera:

Usando las propiedades de los límites en la expresión anterior se obtiene:
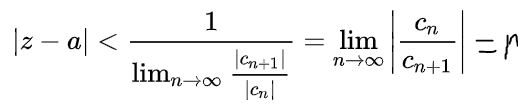
Aquí r es el radio de convergencia y |z – a| r es el círculo de frontera abierta en el plano complejo donde la serie converge. En caso que el valor a y la variable z sean números reales, entonces el intervalo abierto de convergencia sobre el eje real será: (a – r, a+r).
La serie de Taylor de una función f(x) en torno a un valor a en el que la función tiene infinitas derivadas, es una serie de potencias que se define como:
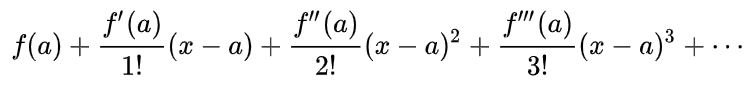
En el entorno | x – a | r, con r como el radio de convergencia de la serie, se tiene que la serie de Taylor y la función f(x) coinciden.
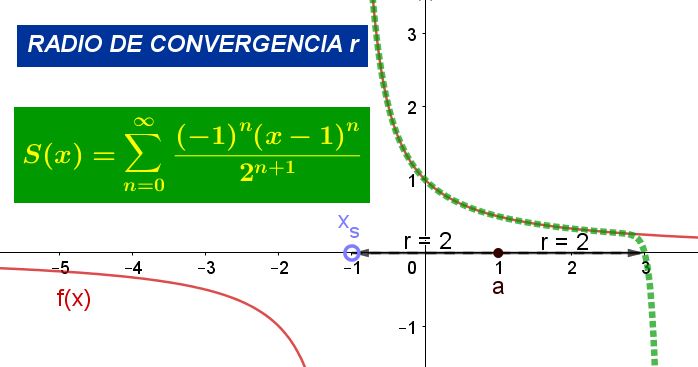
Por otra parte, el radio de convergencia r es la distancia que hay del punto a y la singularidad xs más cercana al punto a, siendo los puntos singulares aquellos valores donde el límite de la función tiende a infinito.
Es decir, que cuando x → xs entonces f → ±∞.
Sea S(x) la serie de potencias dada por la siguiente expresión:
S(x) = 1 – x + x2– x3+ x4– …….+(-1)n ⋅ xn + ….
Para determinar la región donde la serie converge, calculamos el cociente entre el término (n-ésimo + 1) y el término (n-ésimo):
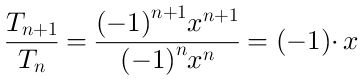
El valor absoluto del cociente anterior es |x| y su límite cuando n → ∞ también es |x|.
Para que la serie sea convergente es necesario que:
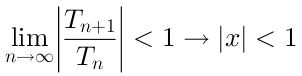
Entonces el radio de convergencia de esta serie es r=1, ya que la misma converge para los valores de x que están a una distancia menor que 1 respecto del centro x = 0.
Se quiere encontrar la serie de Taylor de la función f(x) = 1 / (1 + x) en torno al punto x=0 y determinar su radio de convergencia.
Para encontrar la serie tomamos las derivadas sucesivas de la función f(x), de las cuales mostraremos las tres primeras:
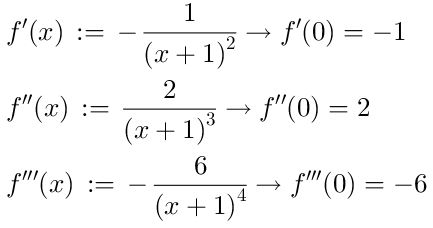
Tomando en cuenta que el término de orden cero de la serie de Taylor es:
f(0)=1,
El de primer orden: f’(0)/1!
Segundo orden:
f’’(0)/2!
Tercer orden:
f’’’(0)/3!
Y así sucesivamente, se tiene que la serie de Taylor de la función dada es:
f(x) = 1 – x + x2 – x3 + x4 – …….+(-1)n ⋅ xn + ….
Que coincide con la serie de potencia estudiada en el ejemplo 1.
Ya hemos dicho que el radio de convergencia de una serie de Taylor es la distancia desde el centro de la expansión en serie, que en nuestro caso es el valor x=0 hasta la primera singularidad de la función f(x).
Como nuestra función tiene una singularidad (es decir, un infinito) en x = -1, la distancia entre el valor -1 y el centro de expansión 0 es |-1 – 0| = 1, se concluye que el radio de convergencia de la serie de Taylor es 1.
Este resultado coincide plenamente con el obtenido en el ejemplo 1 por otro método.
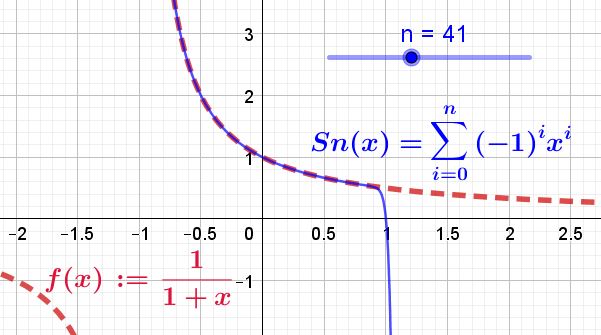
El hecho de que la zona de convergencia de la serie de Taylor sea el intervalo abierto (-1, 1) implica que la función y la serie coinciden en este intervalo, pero no fuera del mismo.
Eso se muestra en la figura 2, donde se han tomado 41 términos de la serie de Taylor, dibujada mediante la línea azul continua, mientras que la función original se muestra en línea roja de segmentos.
Considerar la misma función f(x) = 1 / (1 + x) del ejemplo 2, pero en esta oportunidad se pide hallar la serie de Taylor de dicha función en torno al punto a = 1.
Solución
Hallamos los sucesivos términos coeficientes de la serie, comenzando por el término independiente que es f(1) = ½.
El próximo coeficiente que corresponde al término de primer orden es:
f’(1)/1! = -¼
El de segundo orden es:
f’’(1)/2! = 2/(23 2!)
Sigue el coeficiente de tercer orden:
f’’’(1)/3! = -6 / (24 3!)
Y así sucesivamente. La serie de Taylor será:
Sf(x) = ½ – 1/22 (x-1) + 1/23(x-1)2 – 1/24 (x-1)3 + 1/25 (x-1)4– …..
Hallar el radio de convergencia de la serie anterior
Solución
Escribimos el término n-ésimo y el término n-ésimo más uno:
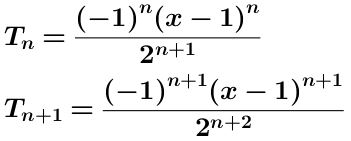
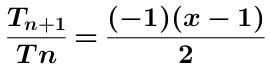
Se toma el valor absoluto de la expresión anterior obteniéndose:
| x – 1 | / 2
Sin embargo, para que la serie sea convergente es necesario que la cantidad anterior sea estrictamente menor que la unidad, es decir:
| x – 1 | 2
Lo que nos indica que el radio de convergencia alrededor del valor x=1 es:
r = 1
Por otra parte, la expresión anterior es equivalente a la doble desigualdad:
-2 x – 1 +2
Si sumamos +1 a cada uno de los tres miembros de la expresión anterior se obtiene:
-1 x 3
Que es el intervalo de convergencia de la serie.
En la figura 1 se muestra la función original y la serie de Taylor de dicha función alrededor del punto x=1. En la figura puede verificarse que la serie coincide con la función en un entorno del punto x=1, pero dentro del radio de convergencia.
- CK-12 Foundation. Series de Potencias: representación de funciones y operaciones. Recuperado de: ck12.org.
- Engler, A. 2019. Cálculo Integral. Universidad Nacional del Litoral.
- Larson, R. 2010. Cálculo de una variable. 9na. Edición. McGraw Hill.
- Mathematics Libre Texts. Power series. Recuperado de: math.liibretexts.org.
- Wikipedia. Series de potencia. Recuperado de: es.wikipedia.org.
- Wikipedia. Radius of convergence. Recuperado de: en.wikipedia.org
