Variación lineal: concepto, ejemplos, ejercicio resuelto
La variación lineal ocurre entre dos magnitudes físicas cuando la gráfica que las representa es una línea recta. Es equivalente a afirmar que las variables están en dependencia lineal, de tal manera que si a una de ellas la llamamos “y” y a la otra “x”, estarán relacionadas mediante la expresión matemática:
y = mx + b
En esta fórmula, m y b son números reales. El valor de m representa la pendiente o inclinación de la recta -que siempre es constante- y b es el corte de la recta con el eje vertical.

Cada fenómeno que responde a una variación lineal tiene diferentes nombres para las variables, como veremos en los siguientes ejemplos. Sin embargo, la forma matemática de la ecuación es la misma.
Experimentalmente se puede establecer si hay una relación lineal entre dos magnitudes, midiendo las parejas de valores (x,y).
Los puntos así obtenidos se grafican en un papel milimetrado y se observa si tienen tendencia lineal, es decir, si hay una recta que se ajuste adecuadamente a los datos experimentales.
En una primera instancia, esta recta se puede trazar visualmente, pero mediante una regresión lineal se pueden encontrar en forma analítica, los valores de m y b de la recta que mejor se ajustan a los puntos experimentales.
Índice del artículo
Existen numerosos fenómenos naturales, así como relaciones establecidas entre patrones de medida, que obedecen a una variación lineal, por ejemplo:
La velocidad en función del tiempo v (t) de un móvil que se desplaza a lo largo de una recta con aceleración constante a y velocidad inicial vo diferente de 0. A este movimiento se le conoce como movimiento rectilíneo uniformemente variado y la ecuación para la velocidad es:
v(t) = vo + at
Otro fenómeno natural cuya variación es lineal es el aumento de longitud que experimentan una varilla o un alambre al calentarse.
En efecto, cuando aumenta la temperatura de cualquier objeto, sus dimensiones también, y este aumento depende del cambio de temperatura ΔT y una cantidad llamada coeficiente de dilatación lineal denotado por la letra griega α:
L = Lo + α ΔT
En esta expresión L es la longitud final del objeto y Lo es su longitud inicial.
Un móvil con velocidad constante se mueve siempre en línea recta. Si la línea recta es el eje horizontal x, la posición x (t) en cualquier instante viene dada por:
x (t) = xo + vt
Donde xo es la posición inicial, v es la velocidad y t es el tiempo. De esta manera se dice que la posición x varía linealmente con el tiempo t.
Médicos y antropólogos pueden estimar la estatura de una persona midiendo la longitud del fémur.
Cuanto más alta es una persona, más largas tiene las piernas, así que hay modelos lineales para predecir la estatura de una persona adulta H (en pulgadas) si se conoce la longitud L (también en pulgadas) de su fémur, de acuerdo a la ecuación:
H = 1.880⋅L + 32.010
Las escalas Celsius y Fahrenheit se utilizan cotidianamente para medir temperaturas. Esta última escala es usada comúnmente en los países de habla inglesa. Hay una equivalencia para pasar de una a otra:
F = (9/5) C + 32
Donde F es la temperatura en grados Fahrenheit y C es la temperatura en grados Celsius.
La presión absoluta P en un fluido incompresible como el agua, cuya densidad constante es ρ, varía en función de la profundidad h como:
P = Po + ρgh
Donde Po es la presión en la superficie libre del líquido. Si el líquido está en un recipiente abierto a la atmósfera, esta presión es simplemente la presión atmosférica Patm, pudiendo escribir entonces:
P = Patm + ρgh
La presión atmosférica a nivel del mar es de aproximadamente 101 kPa. Esta relación entre P y h significa que la presión se incrementa linealmente con la profundidad.

El costo mensual C de manejar un automóvil, incluye un costo fijo mensual Co más el costo del kilometraje o el millaje recorrido cada mes. Un conductor observa que en un mes dado el costo de manejo fue de 380$ por 480 millas, y al mes siguiente fue de 460$ por 800 millas.
Sea d la cantidad de millas recorridas al mes por el conductor, con los datos suministrados, hallar:
a) La variación lineal entre C y d.
b) ¿Cuánto costaría al mes conducir el automóvil en un viaje de 1500 millas?
c) La gráfica de C versus d.
Solución a
Supongamos que las variables tienen una relación dada por:
C = Co + A.d
Donde A y Co son constantes a determinar. A es la pendiente de la recta que representa gráficamente la relación entre C y d. Co es el corte con el eje vertical, el costo fijo mensual que el conductor debe pagar por el solo hecho de tener a la disposición el automóvil. Aquí podrían incluirse gastos de mantenimiento e impuestos, por ejemplo.
Para determinar inequívocamente una recta es necesario conocer su pendiente. Para esto tenemos los puntos:
P1: 480 millas, 380 $
P2: 800 millas, 460 $
Estos puntos, de coordenadas (d,C) o (distancia, costo) son análogos a los puntos de coordenadas (x,y) del plano cartesiano, lo que cambia son los nombres. La pendiente A de la recta entonces viene dada por:
A = (C2 – C1)/(d2 – d1)
A = [(460 – 380) $ / (800 – 480) millas] = (1/ 4) $ / milla
La pendiente de la recta representa el costo por milla, de esta forma:
C = Co + A.d = Co + (1/4).d
Para determinar el costo de base Co se toma esta ecuación y se sustituye uno de los puntos que sabemos le pertenece, por ejemplo P1:
380 $ = Co + [(1/4) $ / milla] . 480 milla → 380 $ = Co + 120 $
Co = 260 $
Ahora podemos formular el modelo de variación lineal como:
C = 260 + (1/4)d
Solución b
El costo mensual de viajar 1500 millas es:
C = 260 + (1/4) x 1500 $ = 635 $
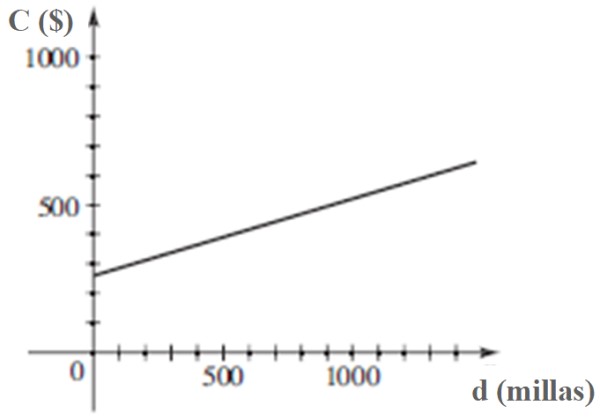
Solución c
La gráfica de C en función de d es:
- Baldor. 1977. Álgebra Elemental. Ediciones Cultural Venezolana.
- Hoekenga, C. Ecuaciones lineales en la Ciencia. Recuperado de: visionlearning.com.
- Hoffman, J. Selección de temas de Matemática. Volumen 2.
- Jiménez, R. 2008. Álgebra. Prentice Hall.
- Stewart, J. 2006. Precálculo: Matemáticas para el Cálculo. 5ta. Edición. Cengage Learning.
- Zill, D. 1984. Álgebra y Trigonometría. McGraw Hill.
