Celda unitaria: propiedades, constantes de red y tipos
La celda unitaria es un espacio o región imaginaria que representa la mínima expresión de un todo; que en el caso de la química, el todo vendría a ser un cristal compuesto de átomos, iones o moléculas, los cuales se ordenan siguiendo un patrón estructural.
En la vida diaria se pueden encontrar ejemplos que encarnan este concepto. Para ello es necesario prestar atención a objetos o superficies que exhiban cierto orden repetitivo de sus elementos. Algunos mosaicos, bajorrelieves, artesonados, sábanas y papeles tapices, pueden englobar en términos generales lo que se entiende por celda unitaria.
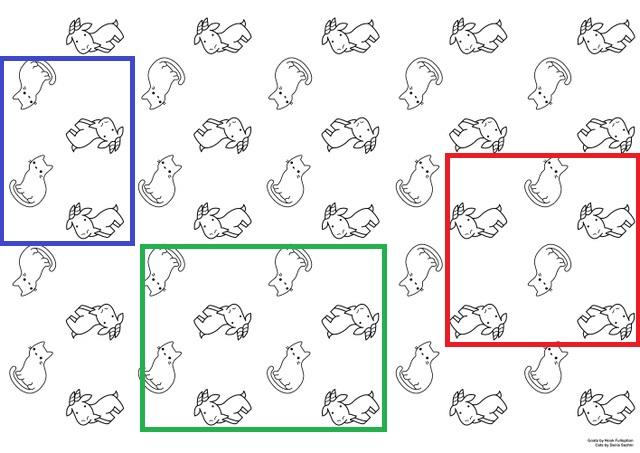
Para ilustrarlo con más claridad, se tiene la imagen superior que podría utilizarse como papel tapiz. En ella aparecen gatos y cabras con dos sentidos alternativos; los gatos están de pies o de cabeza, y las cabras acostadas mirando hacia arriba o hacia abajo.
Estos gatos y cabras establecen una secuencia estructural repetitiva. Para construir todo el papel, bastaría con reproducir la celda unitaria por la superficie un número suficiente de veces, mediante movimientos traslacionales.
Las posibles celdas unitarias se representan con las casillas azul, verde y roja. Cualquiera de estas tres podría utilizarse para obtenerse el papel; pero, es necesario moverlas imaginariamente a lo largo de la superficie para averiguar si reproducen la misma secuencia observada en la imagen.
Empezando por la casilla roja, se apreciaría que si se desplazara tres columnas (de gatos y cabras) hacia la izquierda, ya no aparecería en su parte inferior dos cabras sino solamente una. Por lo tanto, daría lugar a otra secuencia y no puede considerarse como celda unitaria.
Mientras que si movieran imaginariamente las dos casillas, azul y verde, sí se obtendría la misma secuencia del papel. Ambas son celdas unitarias; sin embargo, la casilla azul obedece más la definición, ya que es más pequeña que la casilla verde.
Índice del artículo
- 1 Propiedades de las celdas unitarias
- 2 ¿Qué constantes de red definen una celda unitaria?
- 3 Tipos
- 4 Referencias
Su propia definición, además del ejemplo recién explicado, aclara varias de sus propiedades:
-Si se trasladan en el espacio, sin importar cuál sea la dirección, se obtendrá el sólido o cristal completo. Esto se debe a que, como se mencionó con los gatos y cabras, reproducen la secuencia estructural; lo que es igual a la distribución espacial de las unidades repetitivas.
-Deben ser lo más pequeña posible (u ocupar poco volumen) frente a otras posibles opciones de celdas.
-Son, de ordinario, simétricas. Asimismo, su simetría se refleja literalmente en los cristales del compuesto; si la celda unitaria de una sal es cúbica, sus cristales serán cúbicos. No obstante, hay estructuras cristalinas que se describen con celdas unitarias con geometrías distorsionadas.
-Contienen las unidades repetitivas, las cuales pueden sustituirse por puntos, que a su vez componen tridimensionalmente lo que se conoce como retículo. En el ejemplo anterior los gatos y las cabras representan los puntos reticulares, vistos desde un plano superior; es decir, dos dimensiones.
Las unidades repetitivas o puntos reticulares de las celdas unitarias mantienen la misma proporción de las partículas del sólido.
Si se cuentan el número de gatos y cabras dentro de la casilla azul, se tendrán dos gatos y cabras. Lo mismo ocurre con la casilla verde, y con la casilla roja también (aun si ya se sabe que no es una celda unitaria).
Supóngase por ejemplo que los gatos y las cabras son átomos G y C, respectivamente (una extraña soldadura animal). Como la proporción entre G y C es 2:2 o 1:1 en la casilla azul, puede esperarse, sin equivocaciones, que el sólido tendrá la fórmula GC (o CG).
Cuando el sólido presenta estructuras más o menos compactas, como sucede con las sales, metales, óxidos, sulfuros y aleaciones, en las celdas unitarias no se tienen unidades repetitivas enteras; esto es, hay porciones o partes de las mismas, las cuales suman una o dos unidades.
Esto no es el caso para GC. De serlo, la casilla azul “partiría” a los gatos y cabras en dos (1/2G y 1/2C) o cuatro partes (1/4G y 1/4C). En próximos apartados se verá que en estas celdas unitarias los puntos reticulares están divididos convenientemente de esta y otras maneras.
Las celdas unitarias del ejemplo GC son bidimensionales; sin embargo, esto no aplica en los modelos reales que consideran las tres dimensiones. Así, las casillas o paralelogramos, se transforman en paralelepípedos. Ahora, el término “celda” cobra mayor sentido.
Las dimensiones de estas celdas o paralelepípedos dependen de qué tan largos sean sus lados y ángulos respectivos.
En la imagen inferior se tiene la esquina inferior trasera del paralelepípedo, compuesta por los lados a, b y c, y los ángulos α, β y γ.
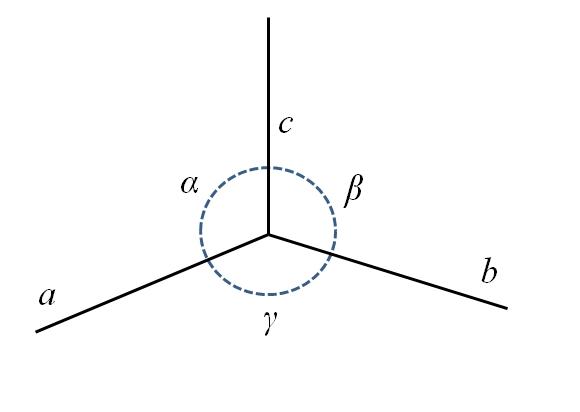
Como puede verse, a es un poco más largo que b y c. En el centro se tiene un círculo con trazo punteado para indicar los ángulos α, β y γ, entre ac, cb y ba, respectivamente. Para cada celda unitaria estos parámetros tienen valores constantes, y definen su simetría y la del resto del cristal.
Aplicando nuevamente algo de imaginación, los parámetros de la imagen definirían una celda parecida a un cubo estirado en su arista a. Así, surgen celdas unitarias con diferentes longitudes y ángulos de sus aristas, las cuales asimismo pueden clasificarse en varios tipos.
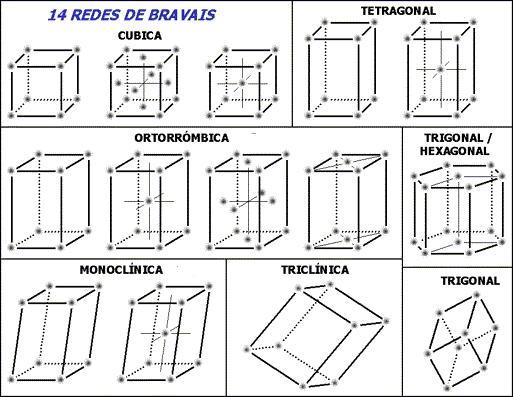
Nótese para empezar en la imagen superior las líneas punteadas dentro de las celdas unitarias: indican el ángulo inferior trasero, tal y como recién se explicó. Puede formularse la siguiente pregunta, ¿dónde están los puntos reticulares o unidades repetitivas? Aunque dan la errónea impresión de que las celdas están vacías, en sus vértices radica la respuesta.
Estas celdas se generan o escogen de tal manera que en sus vértices se sitúen las unidades repetitivas (puntos grisáceos de la imagen). Dependiendo de los valores de los parámetros establecidos en el apartado anterior, constantes para cada celda unitaria, se derivan siete sistemas cristalinos.
Cada sistema cristalino tiene su propia celda unitaria; la segunda define al primero. En la imagen superior hay siete recuadros, correspondientes a los siete sistemas cristalinos; o de manera un poco más resumida, redes cristalinas. Así, por ejemplo, una celda unitaria cúbica corresponde a uno de los sistemas cristalinos que define una red cristalina cúbica.
De acuerdo a la imagen, los sistemas o redes cristalinos son:
-Cúbica
-Tetragonal
-Ortorrómbica
-Hexagonal
-Monoclínica
-Triclínica
-Trigonal
Y dentro de estos sistemas cristalinos surgen otros que componen las catorce redes de Bravais; que entre todas las redes cristalinas, son las más básicas.
En un cubo todos sus lados y ángulos son iguales. Por lo tanto, en esta celda unitaria se cumple lo siguiente:
a = b = c
α = β = γ = 90º
Hay tres celdas unitarias cúbicas: simple o primitiva, centrada en el cuerpo (bcc), y centrada en las caras (fcc). Las diferencias radican en cómo se distribuyen los puntos (átomos, iones o moléculas) y en el número de los mismos.
¿Cuál de estas celdas es la más compacta? Aquella cuyo volumen sea más ocupado por puntos: la cúbica centrada en las caras. Nótese que si sustituyéramos los puntos por los gatos y cabras del principio, estos no estarían confinados a una única celda; pertenecerían y serían compartidos por varias. Nuevamente, se trataría de porciones de G o C.
Número de unidades
Si los gatos o cabras estuvieran en los vértices, serían compartidos por 8 celdas unitarias; es decir, cada celda poseería 1/8 de G o C. Junte o imagine 8 cubos, en dos columnas de dos filas cada una, para visualizarlo.
Si los gatos o cabras estuvieran en las caras, serían compartidos solamente por 2 celdas unitarias. Para verlo, basta con juntar dos cubos.
Por otro lado, si el gato o la cabra estuvieran en el centro del cubo, únicamente pertenecerían a una sola celda unitaria; igual sucede con las casillas de la imagen principal, cuando se abordó el concepto.
Dicho entonces lo anterior, dentro de una celda unitaria cúbica simple se tiene una unidad o punto reticular, ya que posee 8 vértices (1/8 x 8 = 1). Para la celda cúbica centrada en el cuerpo se tiene: 8 vértices, que es igual a un átomo, y un punto o unidad en el centro; por lo tanto, hay dos unidades.
Y para la celda cúbica centrada en las caras se tiene: 8 vértices (1) y seis caras, donde en las cuales se comparten la mitad de cada punto o unidad (1/2 x 6 = 3); por lo tanto, posee cuatro unidades.
Comentarios similares puede hacerse respecto a la celda unitaria para el sistema tetragonal. Sus parámetros estructurales son los siguientes:
a = b ≠ c
α = β = γ = 90º
Los parámetros para la celda ortorrómbica son:
a ≠ b ≠ c
α = β = γ = 90º
Los parámetros para la celda monoclínica son:
a ≠ b ≠ c
α = γ = 90º; β ≠ 90º
Los parámetros para la celda triclínica son:
a ≠ b ≠ c
α ≠ β ≠ γ ≠ 90º
Los parámetros para la celda hexagonal son:
a = b ≠ c
α = β = 90º; γ ≠ 120º
En realidad la celda constituye la tercera parte de un prisma hexagonal.
Y finalmente, los parámetros para la celda trigonal son:
a = b = c
α = β = γ ≠ 90º
- Whitten, Davis, Peck & Stanley. (2008). Química. (8va ed.). CENGAGE Learning P 474-477.
- Shiver & Atkins. (2008). Química Inorgánica. (Cuarta edición). Mc Graw Hill.
- Wikipedia. (2019). Primitive cell. Recuperado de: en.wikipedia.org
- Bryan Stephanie. (2019). Unit Cell: Lattice Parameters & Cubic Structures. Study. Recuperado de: study.com
- Academic Resource Center. (s.f.). Crystal structures. [PDF]. Illinois Institute of Technology. Recuperado de: web.iit.edu
- Belford Robert. (07 de febrero de 2019). Crystal lattices and unit cells. Chemistry Libretexts. Recuperado de: chem.libretexts.org
