Par ordenado: características, ejemplos, ejercicios

¿Qué es un par ordenado?

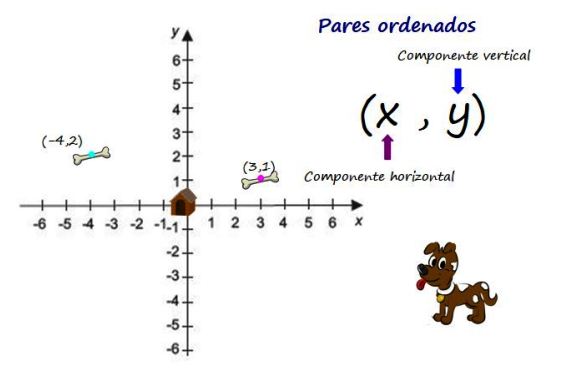
Un par ordenado o dupla es un conjunto de dos elementos que se escriben según el orden establecido por un determinado criterio. Dicho criterio especifica cuál de los dos elementos va primero y cuál va después.

El par ordenado se denota como (x,y), donde “x” es el primer elemento del par y “y” es el segundo, también llamados componentes. En general (x, y) no es el mismo par ordenado (y, x). Y además del orden, otra característica importante de los pares ordenados es la igualdad: dos pares ordenados (a,b) y (c,d) son iguales solamente si a = c y b = d.

Ejemplos de pares ordenados serían los que se componen de la edad y el peso de un curso de alumnos de matemática. El par ordenado (15, 62) corresponde a un alumno de 15 años y 62 kilos, diferente al improbable par (62,15).

El concepto de par ordenado es muy importante en diversas áreas de la matemática, como el plano cartesiano, las fracciones, los vectores en el plano, las relaciones y las funciones. Un  aspecto importante es que sus elementos no tienen que ser necesariamente numéricos, por ejemplo se pueden hacer pares ordenados con:

• País-ciudad capital
• Nombre-apellido
• Esposa-esposo

Y muchas otras combinaciones más.

Ejemplos de pares ordenados

Fracciones

Una fracción se representa como el cociente de dos enteros p/q, por ejemplo la fracción ½, que es equivalente al número decimal 0.5.

Sin embargo, esta fracción no es la única que representa al decimal 0.5, también lo hacen las siguientes:

2/4; 3/6; (–2)/(–4); 20/40; (–1)/(–2)…

De este modo, cualquier fracción se puede representar como un par ordenado (p,q), donde p y q son enteros, con p ocupando la posición del numerador y q la del denominador. Hay una restricción importante y es que q (el denominador) tiene que ser diferente de 0, ya que no están definidas las fracciones de la forma p/0.

Y otra condición importante es que dos fracciones a/b y c/d son iguales siempre y cuando se cumpla que:

a∙d=b∙c

Funciones y sus gráficas

Una función se puede expresar como un conjunto de pares ordenados. Por ejemplo, al graficar una función en el plano cartesiano, al primer elemento se le asigna la posición de la variable independiente, mientras que al segundo se le asigna la variable dependiente. Este es un par ordenado.

Para la función y = f(x), se puede expresar el par ordenado como [x, f(x)]. Por ejemplo, considérese el conjunto de partida:

A= {1, 2, 3, 4}

En este conjunto se encuentran las primeras componentes de un par ordenado según la función y = x². El conjunto de las segundas componentes es:

B ={1, 4, 9, 16}

Y los pares ordenados que se forman son:

{(1,1); (2,4); (3, 9); (4;16)}

Sobre el sistema de coordenadas cartesianas, los pares ordenados representan los puntos que se unen mediante trazo continuo para generar la gráfica de la función.

Vectores en el plano

Los vectores se pueden representar en el plano cartesiano mediante pares ordenados, donde el primer elemento representa la componente horizontal “x” y el segundo la componente vertical “y”. Para distinguir los vectores de los puntos en el plano, se los denota mediante letras negritas y se utilizan los corchetes en vez de los paréntesis, así:

v = x, y >

Por ejemplo, el vector v = 4, 7 > tiene componente horizontal igual a 4 y componente vertical igual a 7. Su gráfica es:

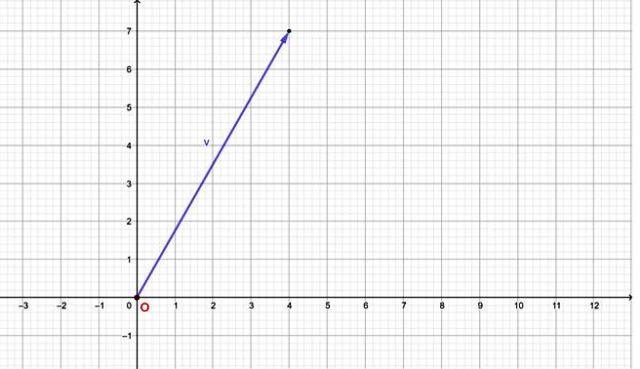
Nótese que este vector tiene su origen coincidiendo con el origen del sistema de coordenadas (0,0). Si el vector tiene su origen en cualquier otro punto, se puede expresar igualmente en forma de par ordenado a través de una resta de pares ordenados, para ello ver los apartados siguientes.

Operaciones con pares ordenados

Adición

Sean los pares ordenados (a,b) y (c,d). Se obtiene un nuevo par ordenado mediante su suma de acuerdo a:

(a,b) + (c,d) = (a+c, b+d)

Elemento neutro

El elemento neutro de la adición de pares ordenados es el par (0,0), ya que cuando se suma al par ordenado (a,b), la suma resulta este último:

(a,b) + (0,0) = (a,b)

Suma del opuesto

Al sumar un par ordenado (a,b) con su opuesto (-a,-b) se obtiene el par ordenado (0,0):

(a,b) + (–a,–b) = (0,0)

Conmutatividad

El orden de los sumandos no altera la suma:

(a,b) + (c,d) = (c,d) + (a,b)

Asociatividad

El resultado de sumar tres pares ordenados no se altera cuando se agrupan para efectuar la operación:

[(a,b) + (c,d)] + (e, f) = (a,b) + [(c,d) + (e, f)]

Sustracción de pares ordenados

Sean los pares ordenados (a,b) y (c,d), la sustracción se lleva a cabo del siguiente modo:

(a,b) – (c,d) = (a–c, b–d)

Producto

En el producto hay dos opciones: i) multiplicar un par ordenado por una constante y ii) multiplicar dos (o más) pares ordenados.

Multiplicación por una constante

Sea k una constante y el par ordenado (a,b), el producto entre la constante y el par es:

k∙(a,b) = (k∙a, k∙b)

Multiplicación de pares ordenados

El producto entre los pares ordenados (a,b) y (c,d) se efectúa de la siguiente manera:

(a,b) x (c,d) = (ac – bd, bc+ad)

Elemento neutro

El elemento neutro de la multiplicación es (1,0), ya que al multiplicar cualquier par ordenado por este, siguiendo la regla de la multiplicación antes descrita, resulta el par original:

(a,b) x (1,0)= (a – 0, b + 0) = (a,b)

Asociatividad

Como el orden de los factores no altera el producto, se puede agrupar de maneras diferentes para multiplicar tres o más pares ordenados y el resultado es el mismo:

[(a,b) x (c,d)] x (e,f) = (a,b) x [(c,d) x (e,f)]

Ejercicios resueltos

Ejercicio 1

Se tienen los pares ordenados (x², x–2) = (16, 2). ¿Cuál es el valor de x?

Solución

Aplicando la igualdad de pares ordenados se obtiene en primer lugar:

x² = 16 ⇒ x₁ = 4, x₂ = –4

Para saber cuál de los dos valores escoger, se hace uso de:

x–2 = 2

x = 2 + 2 = 4

Por lo tanto, el valor pedido de x es 4.

Ejercicio 2

Expresar como un par ordenado el vector que va desde el punto (1, 3) hasta el punto (7, 11) y representarlo gráficamente.

Solución

Sea v el vector buscado. Para determinar el par ordenado que lo representa, y que contiene sus coordenadas, se restan las coordenadas del punto de llegada y el punto de origen, en ese orden. Así:

v = 7-1; 11-3> = 6; 8>

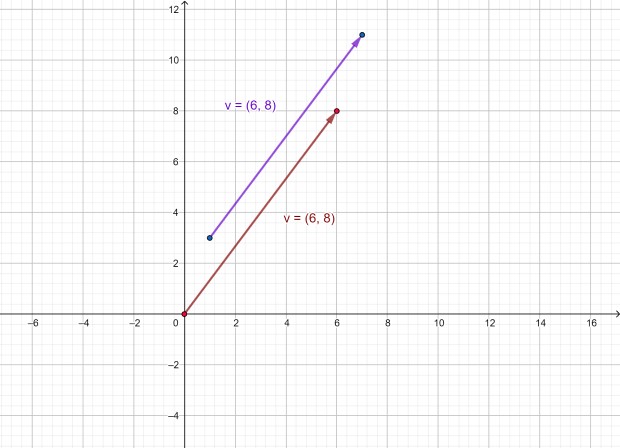
A continuación se representa el vector v como aquel que va desde (1,3) hasta (7, 11) y el vector equipolente v cuyo origen se fija al origen del sistema de coordenadas (0,0). Como se puede ver, tienen la misma dirección y sentido.

Referencias

1. DeepAl. Ordered Pair. Recuperado de: deepai.org.
2. Matemovil. Representación cartesiana de un vector mediante un par ordenado. Recuperado de: matemovil.com.
3. Varsity Tutors. Ordered Pair. Recuperado de: varsitytutors.com
4. Sacerdoti, Juan. Relaciones y funciones. Facultad de Ingeniería. Departamento de Matemáticas. Universidad de Buenos Aires. Recuperado de: materias.fi.uba.ar.
5. University of Denver. Relations. Recuperado de: math.ucdenver.edu.