¿Cuáles son las Partes del Plano Cartesiano?
Las partes del plano cartesiano están compuestas por dos rectas reales, perpendiculares, las cuales dividen al plano cartesiano en cuatro regiones. Cada una de estas regiones se llama cuadrantes y los elementos del plano cartesiano se llaman puntos. El plano, junto con los ejes coordenados, se llama plano cartesiano en honor al filósofo francés René Descartes, quien inventó la geometría analítica.
Las dos rectas (o ejes coordenados) son perpendiculares porque forman un ángulo de 90º entre ellas y se cruzan en un punto común (origen). Una de las rectas es horizontal, siendo denominada origen de la x (o abcisa) y la otra recta es vertical, siendo denominada origen de y (u ordenada).
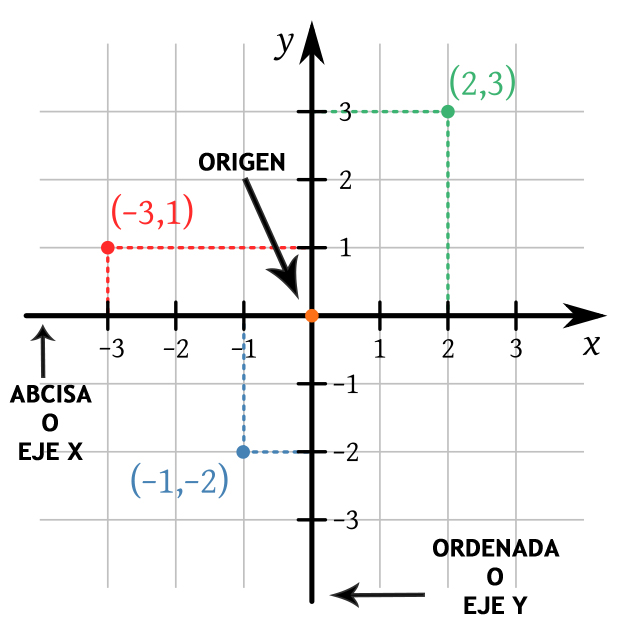
La mitad positiva del eje X está a la derecha del origen y la mitad positiva del eje Y está hacia arriba del origen. Esto permite distinguir los cuatro cuadrantes del plano cartesiano lo cual es muy útil a la hora de graficar puntos en el plano.
Puntos del plano Cartesiano
A cada punto P del plano se le puede asignar un par de números reales los cuales son sus coordenadas cartesianas.
Si una recta horizontal y una recta vertical pasan por P, y estas intersectan al eje X y al eje Y en los puntos a y b respectivamente, entonces las coordenadas de P son (a,b). Se llama a (a,b) un par ordenado y es importante el orden en que se escriben los números.
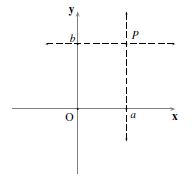
El primer número, a, es la coordenada en “x” (o abscisa) y el segundo número, b, es la coordenada en “y” (u ordenada). Se utiliza la notación P = (a,b).
Es evidente por la forma en que se construyó el plano cartesiano que al origen le corresponden las coordenadas 0 en el eje “x” y 0 en el eje “y”, es decir, O=(0,0).
Cuadrantes del plano cartesiano
Como se aprecia en las figuras anteriores, los ejes coordenados generan cuatro regiones diferentes que son los cuadrantes del plano cartesiano, los cuales son denotados por las letras I, II, III y IV y estos se diferencian entre sí en el signo que poseen los puntos que están en cada uno de ellos.
Cuadrante I
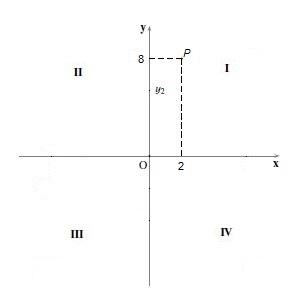
Los puntos del cuadrante I son aquellos que tienen ambas coordenadas con signo positivo, es decir, su coordenada x y su coordenada y son positivas.
Por ejemplo, el punto P=(2,8). Para graficarlo se ubica el punto 2 en el eje “x” y el punto 8 en el eje “y”, luego se trazan las rectas vertical y horizontal respectivamente, y donde se intersecten es donde está el punto P.
Cuadrante II
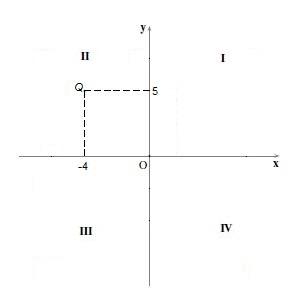
Los puntos del cuadrante II tienen su coordenada “x” negativa y la coordenada “y” positiva. Por ejemplo, el punto Q=(-4,5). Se grafica procediendo como en el caso anterior.
Cuadrante III
En este cuadrante el signo de ambas coordenadas es negativo, es decir, la coordenada “x” y la coordenada “y” poseen son negativas. Por ejemplo, el punto R=(-5,-2).
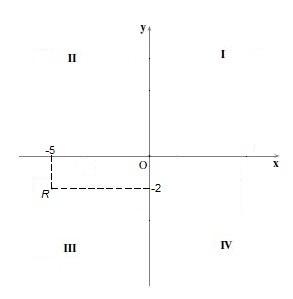
Cuadrante IV
En el cuadrante IV los puntos tienen coordenada “x” positiva y coordenada “y” negativa. Por ejemplo el punto S=(6,-6).
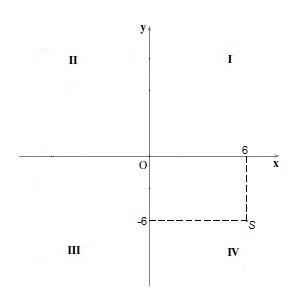
Referencias
- Fleming, W., & Varberg, D. (1991). Algebra y trigonometría con geometría analítica. Pearson Educación.
- Larson, R. (2010). Precalculus (8 ed.). Cengage Learning.
- Leal, J. M., & Viloria, N. G. (2005). Geometría Analítica Plana. Mérida – Venezuela: Editorial Venezolana C. A.
- Oteyza, E. (2005). Geometría Analítica (Segunda ed.). (G. T. Mendoza, Ed.) Pearson Educación.
- Oteyza, E. d., Osnaya, E. L., Garciadiego, C. H., Hoyo, A. M., & Flores, A. R. (2001). Geometría analítica y Trigonometría (Primera ed.). Pearson Educación.
- Purcell, E. J., Varberg, D., & Rigdon, S. E. (2007). Cálculo (Novena ed.). Prentice Hall.
- Scott, C. A. (2009). Cartesian Plane Geometry, Part: Analytical Conics (1907) (reprint ed.). Lightning Source.
