Teorema de Lamy: explicación y ejercicio resuelto
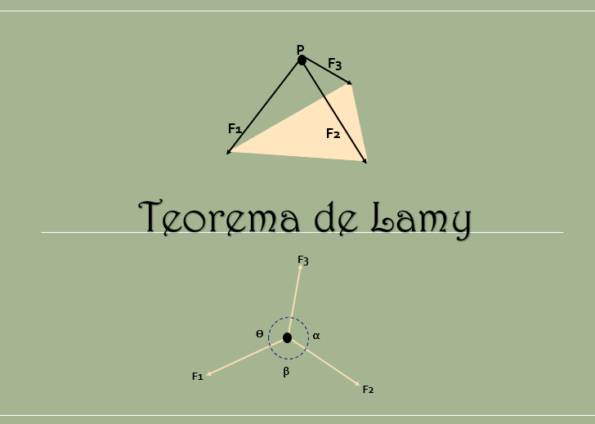
El teorema de Lamy establece que cuando un cuerpo rígido está en equilibrio y sobre la acción de tres fuerzas coplanares (fuerzas que están en un mismo plano), sus líneas de acción concurren en un mismo punto.
El teorema fue deducido por el físico y religioso francés Bernard Lamy y se originó de la ley de los senos. Es muy usado para encontrar el valor de un ángulo, de la recta de acción de una fuerza o para formar el triángulo de fuerzas.
Explicación
El teorema establece que para que pueda cumplirse la condición del equilibrio las fuerzas deben ser coplanares; es decir, la suma de las fuerzas ejercidas sobre un punto es nula.
Además, como se observa en la siguiente imagen, se cumple que al prolongar las líneas de acción de esas tres fuerzas, estas concurren en un mismo punto.
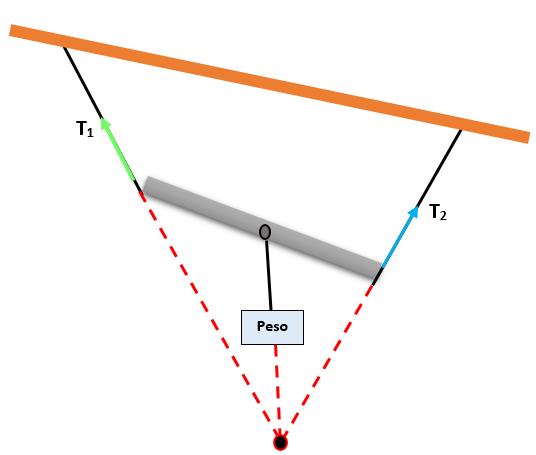
De ese modo si tres fuerzas que están en un mismo plano y son concurrentes, la magnitud de cada fuerza va a ser proporcional al seno del ángulo opuesto, que se forman por las otras dos fuerzas.
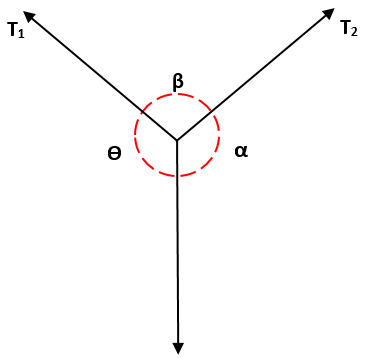
Así se tiene que T1, partiendo del seno de α, es igual a la razón de T2/β, que a su vez es igual a la razón de T3 / Ɵ, es decir:
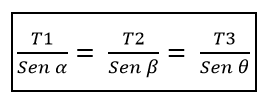
De ahí se deduce que los módulos de esas tres fuerzas deberán ser iguales si los ángulos que forman entre sí cada par de fuerzas son iguales a 120º.
Existe la posibilidad de que uno de los ángulos sea obtuso (mida entre 900 y 1800). En ese caso el seno de ese ángulo será igual al seno del ángulo suplementario (en su par mide 1800).
Ejercicio resuelto
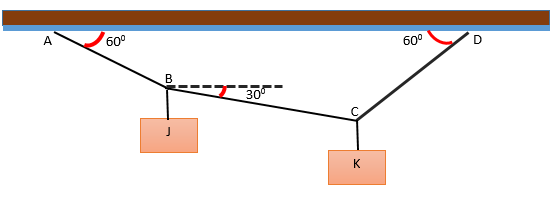
Se tiene un sistema formado por dos bloques J y K, que cuelgan de varias cuerdas formando ángulos respecto a la horizontal, como se muestra en la figura. El sistema se encuentra en equilibrio y el bloque J pesa 240 N. Determinar el peso del bloque K.
Solución
Por el principio de acción y reacción se tiene que las tensiones ejercidas en los bloques 1 y 2 serán igual al peso de estos.
Ahora se construye un diagrama de cuerpo libre para cada bloque y así determinar los ángulos que forman el sistema.
Se sabe que la cuerda que va de A hasta B, tiene un ángulo de 300 , de modo que el ángulo que lo complementa es igual a 600 . De esa forma se llega a 900.
Por otra parte, donde se ubica el punto A, se tiene un ángulo de 600 con respecto a la horizontal; el ángulo entre la vertical y TA va a ser = 1800 – 600 – 900 = 300.
Así se obtiene que el ángulo entre AB y BC = (300 + 900 + 300) y (600 + 900 + 60) = 1500 y 2100. Al sumarse se comprueba que el ángulo total es 3600.
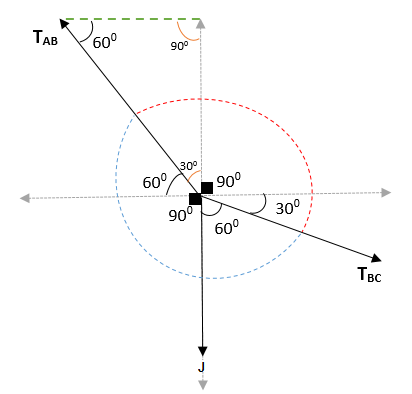
Aplicando el teorema de Lamy se tiene que:
TBC/ sen 1500 = PA/ sen 1500
TBC = PA
TBC = 240N.
En el punto C, donde está el bloque, se tiene que el ángulo entre la horizontal y la cuerda BC es de 300, así que el ángulo complementario es igual a 600.
Por otra parte, se tiene un ángulo de 600 en el punto CD; el ángulo entre la vertical y TC va a ser = 1800 – 900 – 600 = 300.
Así se obtiene que el ángulo en el bloque K es = (300 + 600)
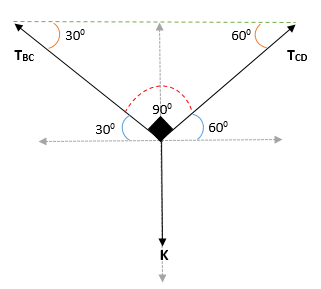
Aplicando el teorema de Lamy en el punto C:
TBC/ sen 1500 = B / sen 900
Q = TBC * sen 900 / sen 1500
Q = 240 N * 1 / 0,5
Q = 480 N.
Referencias
- Ferdinand P. Beer, E. R. (2013). Mecánica para ingenieros, Estática. McGraw-Hill Interamericana.
- Francisco Español, J. C. (2015 ). Problemas resueltos de álgebra lineal. Ediciones Paraninfo, S.A.
- Graham, J. (2005). Fuerza y Movimiento. Houghton Mifflin Harcourt.
- Harpe, P. d. (2000). Topics in Geometric Group Theory. University of Chicago Press.
- P. A Tipler y, G. M. (2005). Física para la Ciencia y la Tecnología. Volumen I. Barcelona: Reverté S.A.
