Números primos: características, ejemplos, ejercicios
Los números primos, también llamados primos absolutos, son aquellos números naturales que únicamente son divisibles entre sí mismos y el 1. En esta categoría entran números como: 2, 3, 5, 7, 11, 13, 17, 19, 23 y muchos más.
En cambio, un número compuesto es divisible por sí mismo, por el 1 y al menos un número más. Tenemos por ejemplo el 12, que es divisible por 1, 2, 4, 6 y 12. Por convención, el 1 no está incluido en la lista de los números primos ni en la de los compuestos.
El conocimiento de los números primos data de tiempos remotos; los antiguos egipcios ya los manejaban y seguramente eran conocidos desde mucho antes.
Estos números son muy importantes, ya que cualquier número natural puede ser representado mediante el producto de números primos, siendo esta representación única, salvo en el orden de los factores.
Este hecho queda plenamente establecido en un teorema llamado teorema fundamental de la aritmética, el cual afirma que los números que no son primos, necesariamente están conformados por productos de números que sí lo son.
Índice del artículo
- 1 Características de los números primos
- 2 Cómo saber si un número es primo
- 3 Formas de encontrar un número primo
- 4 Ejercicios
- 5 Referencias
A continuación las principales características de los números primos:
-Son infinitos, ya que por más grande que sea un número primo, siempre se puede encontrar otro mayor.
-Si un número primo p no divide exactamente a otro número a, se dice entonces que p y a son primos entre sí. Cuando esto sucede, el único divisor común que tienen ambos es el 1.
No es necesario que a sea primo absoluto. Por ejemplo, el 5 es primo, y aunque el 12 no lo es, ambos números son primos entre sí, ya que los dos tienen como divisor común al 1.
-Cuando un número primo p divide a una potencia del número n, también divide a n. Consideremos el 100, que es un potencia de 10, concretamente 102. Ocurre que el 2 divide tanto a 100 como a 10.
-Todos los números primos son impares a excepción del 2, por lo tanto su último dígito es 1, 3, 7 o 9. El 5 no está incluido, porque aunque es impar y primo, nunca es la cifra final de otro número primo. De hecho todos los números que terminan en 5 son múltiplos de este y por lo tanto no son primos.
-Si p es primo y divisor del producto de dos números a.b, entonces p divide a uno de ellos. Por ejemplo, el número primo 3 divide al producto 9 x 11 = 99, ya que 3 es divisor del 9.
La primalidad es el nombre dado a la cualidad de ser primo. Pues bien, el matemático francés Pierre de Fermat (1601-1665) halló una forma de comprobar la primalidad de un número, en el llamado pequeño teorema de Fermat, que dice así:
“Dados un número natural primo p y un número natural cualquiera a mayor que 0, se cumple que ap – a es múltiplo de p, siempre y cuando p sea primo”.
Podemos corroborar esto usando números pequeños, por ejemplo supongamos que p = 4, que ya sabemos que no es primo y a = 6:
64 – 6 = 1296 – 6 = 1290
El número 1290 no es divisible exactamente entre 4, por lo tanto 4 no es número primo.
Hagamos la prueba ahora con p = 5, el cual es primo y a = 6:
65 – 6 = 7766 – 6 = 7760
7760 es divisible entre 5, ya que cualquier número que termina en 0 o en 5 lo es. De hecho 7760/5 = 1554. Como se cumple el pequeño teorema de Fermat, podemos asegurar que 5 es número primo.
La prueba a través del teorema es efectiva y directa con números pequeños, en los cuales la operación sea fácil de realizar, pero ¿qué hacer si nos piden averiguar la primalidad de un número grande?
En ese caso el número se divide sucesivamente entre todos los números primos menores, hasta dar con alguna división exacta o que el cociente sea menor que el divisor.
Si alguna división es exacta, quiere decir que el número es compuesto y si el cociente es menor que el divisor, significa que el número es primo. Lo pondremos en práctica en el ejercicio resuelto 2.
Hay infinitos números primos y no existe una fórmula única para determinarlos. Sin embargo, observando algunos números primos como estos:
3, 7, 31, 127…
Se observa que son de la forma 2n – 1, con n = 2, 3, 5, 7, 9… Nos aseguramos de ello:
22 – 1 = 4 – 1 = 3; 23 – 1 = 8 – 1 = 7; 25 – 1 = 32 – 1 = 31; 27 – 1 = 128 – 1 = 127
Pero no podemos asegurar que en general 2n – 1 sea primo, porque hay algunos valores de n para los cuales no funciona, por ejemplo el 4:
24 – 1= 16 – 1 = 15
Y el número 15 no es primo, ya que termina en 5. No obstante, uno de los números primos más grandes que se conocen, hallado mediante cálculos hechos con computadora, es de la forma 2n – 1 con:
n = 57.885.161
La fórmula de Mersenne nos asegura que 2p – 1 siempre es primo, con tal de que p sea primo también. Por ejemplo, el 31 es primo, entonces es seguro que 231 – 1 lo sea también:
231 – 1 = 2.147.483.647
Sin embargo, la fórmula permite determinar solamente algunos números primos, no todos.
El siguiente polinomio permite encontrar números primos con tal de que n esté comprendido entre 0 y 39:
P(n) = n2 + n + 41
Más adelante, en la sección de ejercicios resueltos hay un ejemplo de su uso.
Eratóstenes fue un físico y matemático de la Antigua Grecia que vivió en el siglo III a.C. Ideó un método gráfico de hallar los números primos que podemos poner en práctica con números pequeños, se llama la criba de Eratóstenes (una criba es como un colador).
-Se colocan los números en una tabla como la que se muestra en la animación.
-Seguidamente se tachan los números pares, excepto el 2 que sabemos que es primo. Todos los demás son múltiplos de este y por consiguiente no son primos.
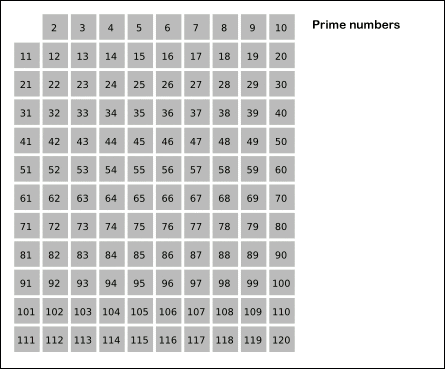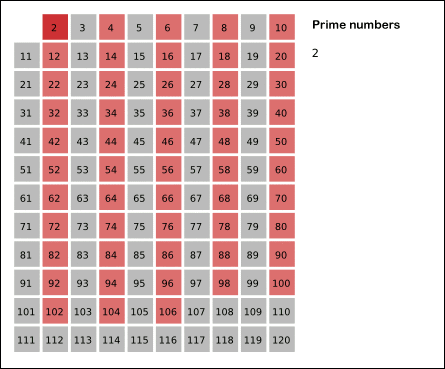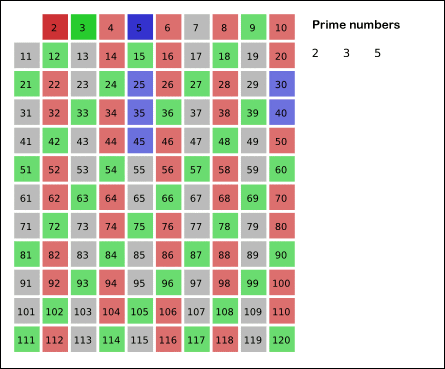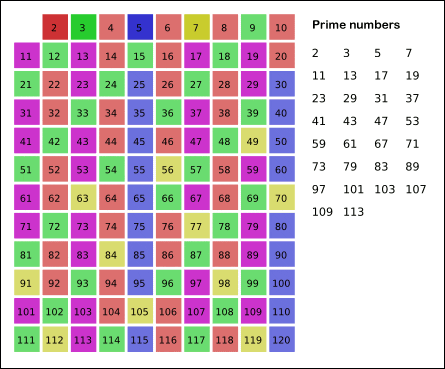
-También se marcan los múltiplos del 3, del 5, del 7 y del 11, excluyéndolos a todos ellos porque sabemos que son primos.
-Los múltiplos de 4, 6, 8, 9 y 10 quedan ya marcados, porque son compuestos y por consiguiente múltiplos de alguno de los primos señalados.
-Por último, los números que quedan sin marcar son primos.
Utilizando el polinomio de Euler para números primos, hallar 3 números mayores que 100.
Solución
Este es el polinomio que Euler propuso para encontrar números primos, el cual funciona para valores de n entre 0 y 39.
P(n) = n2 + n + 41
Mediante tanteo seleccionamos un valor de n, por ejemplo n=8:
P(8) = 82 + 8 + 41 = 113
Como n = 8 produce un número primo mayor que 100, entonces evaluamos el polinomio para n = 9 y n= 10:
P(9) = 92 + 9 + 41 = 131
P(10) = 102 + 10 + 41 = 151
Averiguar si los siguientes números son primos:
a) 13
b) 191
Solución a
El 13 es lo bastante pequeño como para usar el pequeño teorema de Fermat y la ayuda de la calculadora.
Usamos a = 2 para que los números no resulten demasiado grandes, aunque también se pueden usar a=3, 4 o 5:
213 – 2 = 8190
8190 es divisible entre 2, ya que es par, por lo tanto 13 es primo. El lector lo puede corroborar haciendo la misma prueba con a = 3.
Solución b
191 es muy grande como para probar con el teorema y una calculadora común, pero podemos tantear la división entre cada número primo. Omitimos dividir entre 2 porque 191 no es par y la división no va a ser exacta ni el cociente menor que 2.
Probamos a dividir entre 3:
191 /3 = 63,666…
Y no da exacto, ni el cociente es menor que el divisor (63,666… es mayor que 3)
Seguimos probando así a dividir 191 entre los primos 5, 7, 11, 13 y tampoco se llega a la división exacta, ni el cociente menor que el divisor. Hasta que se divide entre 17:
191 / 17 = 11, 2352…
Como no es exacta y 11,2352… es menor que 17, el número 191 sí es primo.
- Baldor, A. 1986. Aritmética. Ediciones y Distribuciones Códice.
- Prieto, C. Los números primos. Recuperado de: paginas.matem.unam.mx.
- Properties of prime numbers. Recuperado de: mae.ufl.edu.
- Smartick. Números primos: cómo encontrarlos con la criba de Eratóstenes. Recuperado de: smartick.es.
- Wikipedia. Número primo. Recuperado de: es.wikipedia.org.
