Equilibrio rotacional: fórmulas y ecuaciones, ejemplos, ejercicios
Se afirma que un cuerpo extendido está en equilibrio rotacional cuando la suma de los torques que actúan sobre él es nula. Esto no significa que el objeto necesariamente esté en reposo, sino más bien que no hay tendencia neta a cambiar su estado de movimiento por otro.
Un objeto que se mueve con velocidad constante lo hace a lo largo de una línea recta y podemos considerarlo en equilibrio rotacional. Ahora bien, los objetos giran porque hay fuerzas que actúan sobre ellos de una manera tal que resulta una rotación. La capacidad de una fuerza para producir rotación, llamada torque o torca, depende no solo de la intensidad de la fuerza, sino también de dónde esté aplicada.

Esto lo reconocemos de inmediato cuando se va a abrir una puerta cerrada: nunca se aplica la fuerza cerca de las bisagras, sino lejos de ellas, por eso la manija se coloca lo más lejos posible, al lado contrario de la puerta.
Por las bisagras pasa el eje de rotación de la puerta. Insistiendo en empujarla muy cerca de las bisagras, hay que hacer un esfuerzo grande para que la puerta se mueva siquiera un poco.
En la literatura se encuentra al torque con diferentes nombres: momento de torsión, torsión, momento de una fuerza y torca. Todos son sinónimos.
Entonces, necesitamos conocer los torques que actúan sobre un objeto para establecer la condición de equilibrio de rotación.
Índice del artículo
- 1 Condición de equilibrio rotacional
- 2 Fórmulas y ecuaciones
- 3 Ejemplos
- 4 Ejercicio resuelto
- 5 Referencias
La condición de equilibrio rotacional es:
La suma de todos los momentos o torques que actúan sobre un cuerpo, calculados respecto a cualquier eje, debe ser nula.
El objeto en cuestión debe ser extendido, ya que las partículas, por definición, solamente tienen equilibrio de traslación.
Puede haber fuerzas aplicadas sobre el cuerpo y aún así existir equilibrio rotacional, mientras que las fuerzas no lo hagan girar.
También puede haber movimiento, incluso acelerado, pero siempre a lo largo de una línea recta, ya que no todas las fuerzas causan la aparición de torques. Estos aparecen cuando las fuerzas no actúan todas a lo largo de la misma línea de acción.
El torque se denota con la letra griega τ, en negrita porque se trata de un vector y así la distinguimos de su magnitud o módulo, que es un escalar. Depende de la fuerza aplicada F, del vector r que se dirige desde el eje de rotación O hasta el punto de aplicación de la fuerza y por último, del ángulo entre estos dos vectores.
Mediante el producto vectorial se establece la relación adecuada entre estas magnitudes:
τ = r x F
Y el módulo del torque, denotado sin negrita es:
τ = r⋅F⋅sen θ
Donde θ es el ángulo entre r y F. Las unidades del torque son simplemente N⋅m en el Sistema Internacional.
En la figura hay una llave inglesa con la que se pretende hacer girar una tuerca en sentido antihorario (contrario a las agujas del reloj). Para esto se prueba con dos fuerzas FA y FB.
FA está más cerca de O y tiene un vector rA o brazo de palanca más corto, por lo tanto no produce tanto torque como la fuerza FB, que tiene igual magnitud, pero tiene un vector rB más grande.
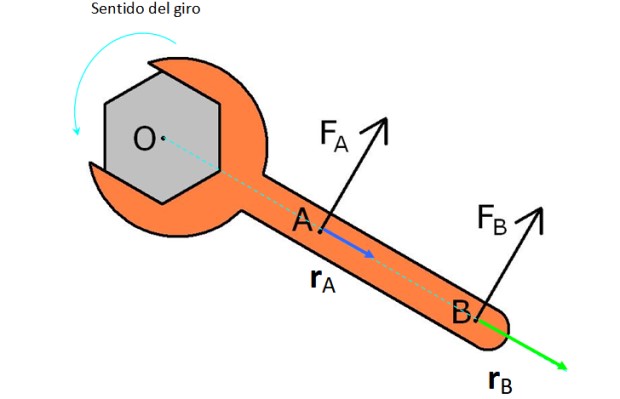
Nótese que si se quiere hacer girar la tuerca en sentido horario, hay que aplicar las fuerzas en sentido opuesto a como aparecen en la figura.
Dirección y sentido del torque
Como el torque resulta del producto cruz entre los vectores fuerza y posición, y estos se encuentran en el plano de la llave inglesa, el torque tiene que ser un vector perpendicular a dicho plano, es decir, dirigido hacia el lector o hacia dentro de la página.
Por convención, el torque es positivo si produce giro en sentido opuesto a las agujas del reloj, y negativo si lo hace en el sentido del reloj.
La dirección y el sentido del torque resultante se determinan fácilmente mediante la regla de la mano derecha que se muestra a continuación:
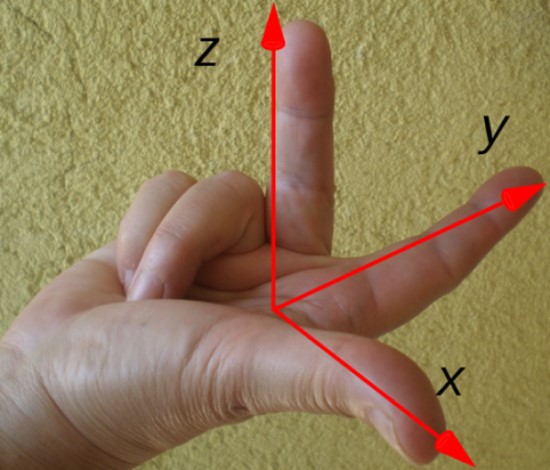
El dedo índice apunta según el vector de posición r, el dedo medio según la fuerza F y el dedo pulgar señala la dirección y el sentido del torque τ. En este ejemplo, el torque está dirigido a lo largo del eje x, según el dibujo de los ejes coordenados.
Si sobre un cuerpo actúan los torques τ1, τ2, τ3 … τi, el torque neto o resultante τn es la suma vectorial de todos ellos:
τn = τ1+ τ2 + τ3 + … τi
Con notación de sumatoria queda:
τn = ∑ τi
La condición de equilibrio se expresa matemáticamente así:
τn = 0
O bien:
∑ τi = 0
Donde el torque τ, respecto a un determinado eje O, se calcula mediante:
τ = r x F
Y cuya magnitud es:
τ = r⋅F⋅sen θ
-En humanos y animales, el peso es una fuerza que puede causar torque y hacer girar y caer.
Las personas por lo general mantienen una postura tal que al caminar, las mantiene en equilibrio de rotación, salvo que se practique actividad deportiva, como gimnasia, patinaje o deportes en general.
-Dos niños que se las arreglaron para mantenerse horizontales en el balancín o sube y baja están en equilibrio de rotación.
-Cuando los platillos de la balanza están equilibrados, el sistema está en equilibrio rotacional.
-Los avisos y los semáforos que cuelgan en calles y avenidas también se encuentran en equilibrio rotacional. Si los cables que los sujetan se rompen, este equilibrio se pierde y el aviso queda colgando o cae.
-Los puentes colgantes como el Golden Gate en San Francisco y el puente de la figura 1.
La barra apoyada en un soporte mostrada en la figura es muy liviana. La fuerza que ejerce el soporte es F y en el extremo derecho se aplica la fuerza A.
Se pide calcular las magnitudes de dichas fuerzas considerando que el sistema está en equilibrio de traslación y de rotación.
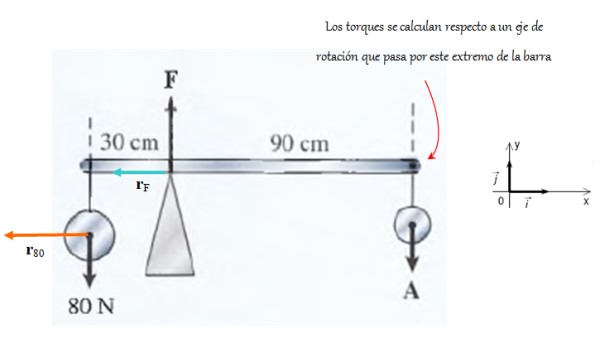
Solución
Como el sistema no se traslada, la sumatoria de fuerzas se anula. Todas son verticales y se pueden trabajar con las magnitudes. El sentido positivo es hacia arriba y el negativo hacia abajo, por lo tanto:
F – 80 – A = 0
Ahora se aplica la condición de equilibrio rotacional, para lo cual hay que escoger un eje de rotación arbitrario. En este caso se escoge en el extremo derecho, para que el vector rA sea nulo, de esta manera no aparece el torque ejercido por A, sino únicamente los de F y la fuerza de la izquierda.
El torque producido por F es, según la regla de la mano derecha y el sistema coordenado que se muestra:
τF = rF x F = 0.9 F (–k) N.m
Está dirigido hacia dentro de la pantalla y lleva signo negativo. Mientras que el torque producido por la fuerza de 80 N es:
τ = 80 x 1.20 (k) N⋅m = 96 (k) N⋅m
Este torque está dirigido hacia fuera de la pantalla y se le asigna signo positivo. Como existe equilibrio rotacional:
96 – 0.9⋅F = 0
La magnitud de F es:
F = (96/0.9) N = 106.7 N
Y como el sistema está en equilibrio de traslación, la sumatoria de las fuerzas se anula. Esto nos permite despejar la magnitud de A:
F – A – 80 N = 0
Por lo tanto:
A = 106.7 – 80 N = 26.7 N.
- Rex, A. 2011. Fundamentos de Física. Pearson.
- Serway, R., Jewett, J. (2008). Física para Ciencias e Ingeniería. Volumen 1. 7ma. Ed. Cengage Learning.
- Sears, Zemansky. 2016. University Physics with Modern Physics. 14th. Ed. Volume 1. Pearson.
- Tipler, P. (2006) Física para la Ciencia y la Tecnología. 5ta Ed. Volumen 1. Editorial Reverté.
- Tippens, P. 2011. Física: Conceptos y Aplicaciones. 7ma Edición. McGraw Hill.
