Fuerza elástica: en qué consiste, fórmulas y ejercicios
La fuerza elástica es la fuerza que un objeto ejerce para resistir a un cambio en su forma. Se manifiesta en un objeto que tiende a recuperar su forma cuando está bajo la acción de una fuerza de deformación.
A la fuerza elástica también se le llama fuerza restauradora porque se opone a la deformación para retornar los objetos a su posición de equilibrio. La transferencia de la fuerza elástica es a través de las partículas que integran los objetos.
Por ejemplo, cuando se comprime un resorte metálico se ejerce una fuerza que empuja las partículas del resorte disminuyendo la separación entre ellas, al mismo tiempo, las partículas se resisten a ser empujadas ejerciendo una fuerza contraria a la compresión.
Si en vez de comprimir el resorte se tira, estirándose, las partículas que lo integran se separan más. Así mismo, las partículas se resisten a separarse ejerciendo una fuerza contraria al estiramiento.
Los objetos que tienen la propiedad de recuperar su forma original al oponerse a la fuerza de deformación se llaman objetos elásticos. Los resortes, gomas elásticas y cuerdas elásticas son ejemplos de objetos elásticos.
Índice del artículo
La fuerza elástica (Fk) es la fuerza que un objeto ejerce para recuperar su estado de equilibrio natural al haber sido afectado por una fuerza externa.
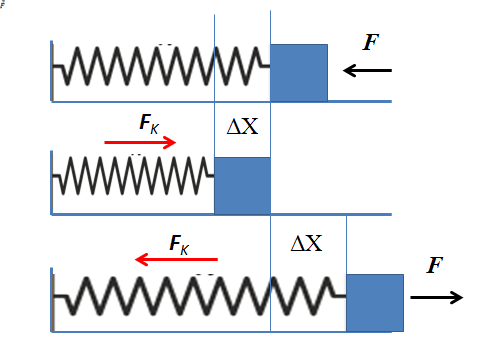
Para analizar la fuerza elástica se tomará en cuenta el sistema ideal masa resorte que consiste en un resorte colocado horizontalmente sujeto de un extremo en la pared y del otro extremo a un bloque de masa despreciable. No se tomará en cuenta las demás fuerzas que actúan sobre el sistema como lo son la fuerza de fricción o la fuerza de gravedad.
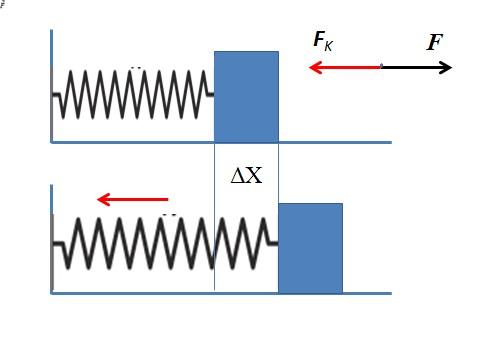
Si se ejerce una fuerza horizontal sobre la masa, dirigida hacia la pared, esta se transfiere hacia el resorte comprimiéndolo. El resorte se desplaza de su posición de equilibrio hacia una nueva posición. Como el objeto tiende a permanecer en equilibrio, se manifiesta la fuerza elástica en el resorte que se opone a la fuerza aplicada.
El desplazamiento indica cuánto se ha deformado el resorte y la fuerza elástica es proporcional a ese desplazamiento. A medida que se comprime el resorte la variación de la posición va aumentando y en consecuencia aumenta la fuerza elástica.
Mientras más se comprime el resorte más fuerza de oposición ejerce hasta llegar a un punto en el cual la fuerza aplicada y la fuerza elástica se equilibran, en consecuencia el sistema masa resorte deja de moverse. Al dejar de aplicar fuerza la única fuerza que actúa es la fuerza elástica. Esta fuerza acelera el resorte en dirección contraria a la deformación hasta recuperar el estado de equilibrio.
De la misma forma ocurre al estirar el resorte halando la masa horizontalmente. El resorte se estira e inmediatamente ejerce una fuerza proporcional al desplazamiento oponiéndose al estiramiento.
La fórmula de la fuerza elástica se expresa mediante la Ley de Hooke. Esta Ley establece que la fuerza elástica lineal ejercida por un objeto es proporcional al desplazamiento.
Fk =-k.Δs [1]
Fk = Fuerza elástica
k = Constante de proporcionalidad
Δs = Desplazamiento
Cuando el objeto se desplaza horizontalmente, como el caso del resorte sujeto a la pared, el desplazamiento es Δx, y la expresión de la Ley de Hooke se escribe:
Fk =-k.Δx [2]
El signo negativo en la ecuación indica que la fuerza elástica del resorte está en dirección opuesta a la fuerza que originó el desplazamiento. La constante de proporcionalidad k es una constante que depende del tipo de material del que está constituido el resorte. La unidad de la constante k es N/m.
Los objetos elásticos tienen un límite de elasticidad que va a depender de la constante de deformación. Si se estira más allá del límite elástico, se deformará de forma permanente.
La ecuación [1] y [2] se aplica a pequeños desplazamientos del resorte. Cuando los desplazamientos son mayores se adicionan términos con mayor potencia de Δx.
La fuerza elástica realiza trabajo sobre el resorte desplazándolo hacia su posición de equilibrio. Durante ese proceso la energía potencial del sistema masa resorte aumenta. La energía potencial debida al trabajo realizado por la fuerza elástica se expresa en la ecuación [3].
U=½ k . Δx2 [3]
La energía potencial se expresa en Joules (J).
Al dejar de aplicar la fuerza de deformación el resorte acelera hacia la posición de equilibrio disminuyendo la energía potencial y aumentando la energía cinética.
La energía cinética del sistema masa resorte, cuando alcanza la posición de equilibrio, se determina mediante ecuación [4].
Ek= ½ m.v2 [4]
m = masa
v = velocidad del resorte
Para resolver el sistema masa resorte se aplica la segunda ley de Newton tomando en cuenta que la fuerza elástica es una fuerza variable.
¿Cuánta fuerza es necesaria aplicar a un resorte para que se estire 5cm si la constante del resorte es de 35N/m?
Como la fuerza de aplicación es opuesta a la fuerza elástica se determina Fk suponiendo que el resorte se estira horizontalmente. El resultado no requiere del signo negativo ya que solo se necesita la fuerza de aplicación.
Ley de Hooke
Fk = -k.Δx
La constante k del resorte es 35N/m.
Δx = 5cm = 0,05m
Fk = -35N/m . 0,05m
Fk = – 1,75N = – F
Se necesita 1,75 N de fuerza para deformar el resorte 5cm.
¿Cuál es la constante de deformación de un resorte que se estira 20 cm por la acción de una fuerza de 60N?
Δx =20cm =0,2m
F = 60N
Fk = -60N = – F
k = – Fk / Δx
= -(-60N)/0,2m
k = 300 N/m
La constante del resorte es 300N/m
¿Cuál es la energía potencial referida al trabajo realizado por la fuerza elástica de un resorte que se comprime 10cm y su constante de deformación es 20N/m?
Δx =10 cm = 0,1m
k =20 N/m
Fk = -20N/m . 0,1m
Fk = -200N
La fuerza elástica del resorte es -200N.
Esta fuerza realiza trabajo sobre el resorte para desplazarlo hacia su posición de equilibrio. Al realizar este trabajo aumenta la energía potencial del sistema.
La energía potencial se calcula con la ecuación [3]
U=½ k . Δx2
U=½(20N/m) . (0,1m)2
U = 0,1Joules
- Kittel, C, Knight, W D y Ruderman, M A. Mechanics. US : Mc Graw Hill, 1973, Vol. I.
- Rama Reddy, K, Badami, S B y Balasubramanian, V. Oscillations and Waves. India : Universities Press, 1994.
- Murphy, J. Physics: understanging the properties of matter and energy. New York : Britannica Educational Publishing, 2015.
- Giordano, N J. College Physics: Reasoning and Relationships. Canada : Brooks/Cole, 2009.
- Walker, J, Halliday, D y Resnick, R. Fundamentals of Physics. US : Wiley, 2014.
