Triángulos: historia, elementos, clasificación, propiedades
Los triángulos son figuras geométricas planas y cerradas, que constan de tres lados. Un triángulo se determina mediante tres rectas que se corten dos a dos, formando entre sí tres ángulos. La forma triangular, llena de simbolismo, está presente en incontables objetos y como elemento de la construcción.
El origen del triángulo se pierde en la historia. A partir de la evidencia arqueológica se sabe que la humanidad primitiva lo conocía bien, pues los restos arqueológicos confirman que era utilizado en herramientas y armas.

También es evidente que los antiguos egipcios poseían sólidos conocimientos de la geometría y en particular de la forma triangular. Los mismos quedaron plasmados en los elementos arquitectónicos de sus construcciones monumentales.
En el papiro Rhind se encuentran fórmulas para el cálculo de áreas de triángulos y trapecios, así como algunos volúmenes y otros conceptos de trigonometría rudimentaria.
Por su parte, se sabe que los babilonios eran capaces de calcular el área del triángulo y otras figuras geométricas, que utilizaban para fines prácticos, como las divisiones de los terrenos. También eran conocedores de muchas propiedades de los triángulos.
No obstante, fueron los antiguos griegos quienes sistematizaron muchos de los conceptos geométricos frecuentes hoy en día, si bien mucho de ese saber no fue exclusivo, ya que con toda seguridad era compartido con estas otras civilizaciones antiguas.
Índice del artículo
- 1 Elementos del triángulo
- 2 Tipos de triángulos
- 3 Propiedades
- 4 Teoremas
- 5 El área de un triángulo
- 6 Ejemplos de triángulos
- 7 Ejercicios
- 8 Referencias
Los elementos de un triángulo cualquiera se indican en la siguiente figura. Son tres: vértices, lados y ángulos.
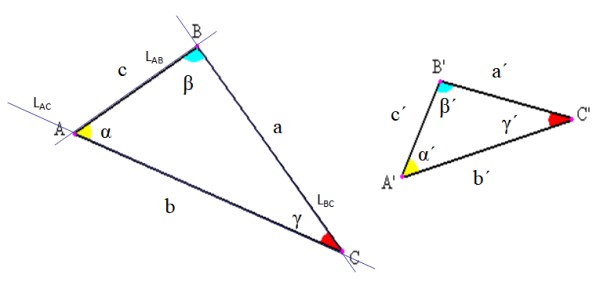
-Vértices: son los puntos de intersección de las rectas cuyos segmentos determinan el triángulo. En la figura superior por ejemplo, la recta LAC que contiene al segmento AC, intersecta a la recta LAB que contiene al segmento AB justamente en el punto A.
–Lados: entre cada pareja de vértices se dibuja un segmento de recta que constituye un lado del triángulo. Este segmento se puede denotar con las letras de los extremos o usando una letra específica para llamarlo. En el ejemplo de la figura 2, el lado AB también es llamado “c”.
–Ángulos: Entre cada lado con un vértice común se origina un ángulo, cuyo vértice coincide con el del triángulo. Generalmente el ángulo se denota con una letra griega, tal como se dijo al comienzo.
Para construir un triángulo en particular, con una forma y tamaño dados, basta con tener alguno de los siguientes conjuntos de datos:
-Los tres lados, bastante obvio tratándose de un triángulo.
-Dos lados y el ángulo entre ellos, y de inmediato se dibuja el lado restante.
-Dos ángulos (internos) y el lado comprendido entre ellos. Por extensión se dibujan los dos lados faltantes y el triángulo queda listo.
Generalmente en la notación de triángulos se utilizan las siguientes convenciones: los vértices se indican con letras latinas mayúsculas, los lados con letras latinas minúsculas y los ángulos mediante letras griegas (ver figura 2).
De esta manera se nombra al triángulo según sus vértices. Por ejemplo el triángulo de la izquierda en la figura 2 es el triángulo ABC, y el de la derecha es el triángulo A´B´C´.
También es posible usar otras notaciones; por ejemplo, el ángulo α en la figura 2 se denota como BAC. Nótese que la letra del vértice va en el medio y las letras se escriben en sentido contrario a las agujas del reloj.
Otras veces se coloca un acento circunflejo para denotar el ángulo:
α = ∠A
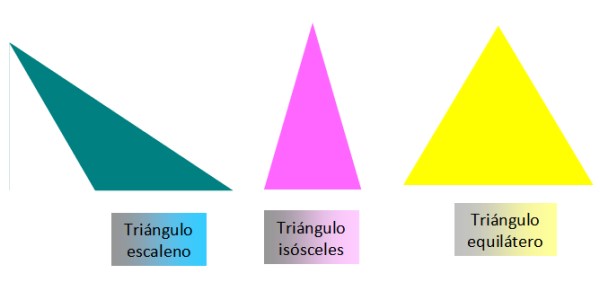
Existen varios criterios de clasificación de triángulos. Lo más usual es clasificarlos según la medida de sus lados o según la medida de sus ángulos. Según la medida de sus lados, los triángulos pueden ser: escalenos, isósceles o equiláteros:
-Escaleno: sus tres lados son diferentes.
-Isósceles: tiene dos lados iguales y uno diferentes.
-Equilátero: los tres lados son iguales.
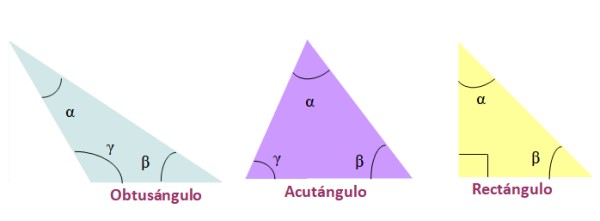
De acuerdo a la medida de sus ángulos, los triángulos se denominan así:
–Obtusángulo, si uno de los ángulos internos es mayor que 90º.
–Acutángulo, cuando los tres ángulos internos del triángulo son agudos, es decir, menores de 90º
–Rectángulo, en caso de que uno de sus ángulos internos valga 90º. Los lados que forman 90º se denominan catetos y el lado opuesto al ángulo recto es la hipotenusa.
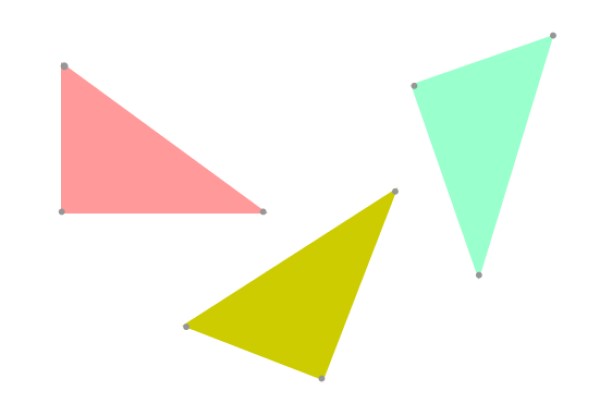
Cuando dos triángulos tienen la misma forma y son de igual tamaño se dice que son congruentes. Por supuesto la congruencia está relacionada con la igualdad, ¿entonces por qué en geometría se habla de “dos triángulos congruentes” en vez de “dos triángulos iguales”?
Bien, se prefiere emplear el término “congruencia” para apegarse a la verdad, ya que dos triángulos pueden tener la misma forma y tamaño, pero estar orientados de manera diferente en el plano (ver figura 3). Desde el punto de vista de la geometría, ya no serían estrictamente iguales.
Criterios de congruencia
Dos triángulos son congruentes si ocurre alguna de las siguientes situaciones:
-Los tres lados miden lo mismo (nuevamente esto es lo más obvio).
-Tienen dos lados idénticos y con el mismo ángulo entre ellos.
-Ambos poseen dos ángulos internos idénticos y el lado comprendido entre dichos ángulos mide lo mismo.
Como puede verse, se trata de que los dos triángulos cumplan las condiciones necesarias para que al construirlos, su forma y tamaño sean exactamente iguales.
Los criterios de congruencia son muy útiles, ya que en la práctica, innumerables piezas y partes mecánicas deben fabricarse en serie, de forma tal que sus medidas y forma sean exactamente las mismas.
Un triángulo es semejante a otro si tienen la misma forma, aunque sean de distinto tamaño. Para asegurarse que la forma es la misma, se requiere que los ángulos internos tengan el mismo valor y que los lados sean proporcionales.
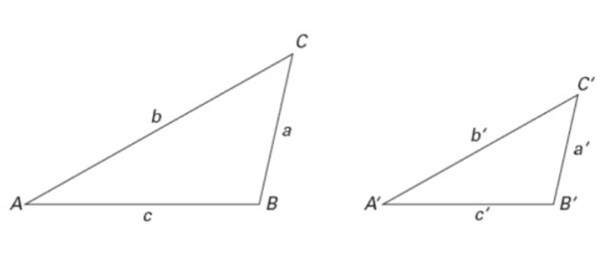
Los triángulos de la figura 2 también son semejantes, así como los de la figura 6. De esta forma:
∠ A = ∠ A´, ∠ B = ∠ B´ y ∠ C = ∠ C´
En cuanto a los lados, se cumplen las razones de semejanza siguientes:
a /a´ = b/b´ = c/c´
Las propiedades fundamentales de los triángulos son las siguientes:
-La suma de los ángulos internos de cualquier triángulo siempre es 180º.
-Para cualquier triángulo, la suma de sus ángulos externos es igual a 360°.
– Un ángulo externo de un triángulo es igual a la suma de los dos ángulos interiores no adyacentes a dicho ángulo.
Se le atribuyen al filósofo y matemático griego Tales de Mileto, quien desarrolló varios teoremas relativos a la geometría. El primero de ellos establece lo siguiente:
Si varias rectas paralelas cortan a dos rectas transversales, en ellas se determinan segmentos que son proporcionales.
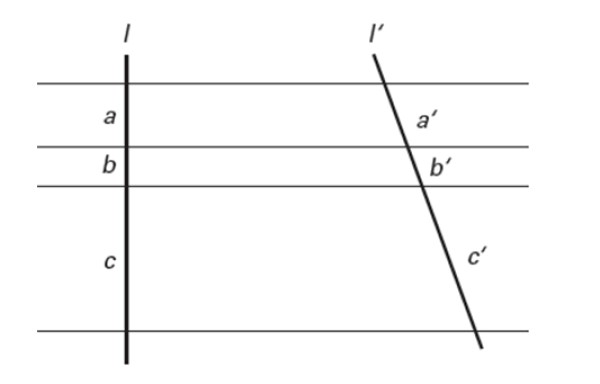
En otras palabras:
a/a´ = b/b´ =c /c´
El primer teorema de Tales es aplicable a un triángulo, por ejemplo se tiene el triángulo azul ABC de la izquierda, el cual se corta por las paralelas rojas a la derecha:
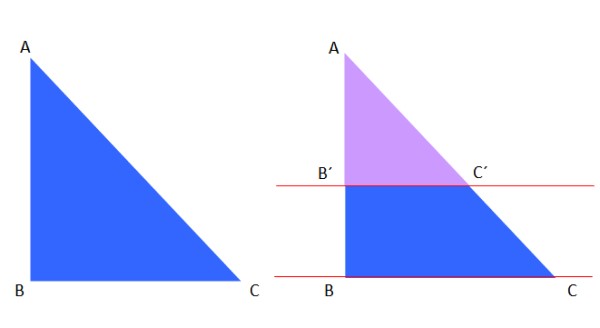
El triángulo AB´C´ de color violeta es semejante al triángulo azul ABC, por lo tanto, de acuerdo al teorema de Tales, se puede escribir lo siguiente:
AB´/AC´ = AB/AC
Y es acorde con lo explicado anteriormente en el segmento de la semejanza de triángulos. Por cierto, las rectas paralelas también pueden ser verticales o bien paralelas a la hipotenusa y de igual modo se obtienen triángulos semejantes.
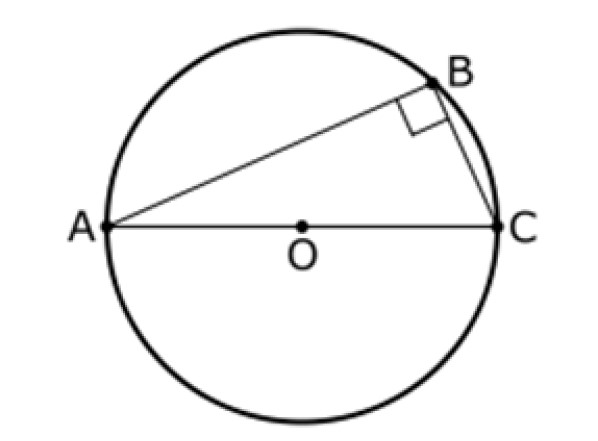
Este teorema también se refiere a un triángulo y una circunferencia de centro O, como los que se muestran a continuación. En esta figura, AC es un diámetro de la circunferencia y B es un punto de ella, siendo B distinto de A y de B.
El segundo teorema de Tales afirma que:
El ángulo entre los segmentos AB y BC siempre es de 90º, por lo tanto el triángulo ABC es rectángulo.
Este es uno de los teoremas más famosos de la historia. Se debe al matemático griego Pitágoras de Samos (569 – 475 a. C.) y es aplicable a un triángulo rectángulo. Dice así:
La suma de los cuadrados de las longitudes los catetos de triángulo rectángulo, es igual a la longitud de la hipotenusa elevada al cuadrado.
Si tomamos como ejemplo el triángulo azul de la figura 8, o el triángulo violeta, pues ambos son rectángulos, entonces se puede afirmar que:
AC2 = AB2 + BC2 (triángulo azul)
AC´2 = AB´2 + BC´2 (triángulo violeta)
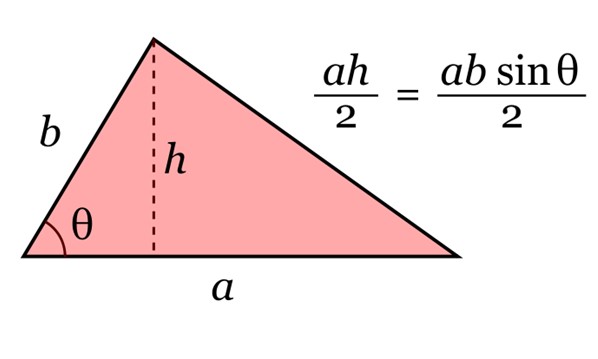
El área del triángulo viene dada por el producto de su base a y su altura h, dividido entre 2. Y por trigonometría, dicha altura se puede escribir como h = b senθ.
Se cuenta que mediante su primer teorema, Tales logró medir la altura de la Gran Pirámide en Egipto, una de las 7 maravillas del mundo antiguo, midiendo la sombra que esta proyectaba en el suelo y la que proyectaba una estaca clavada en el suelo.
Este es el esquema del procedimiento seguido por Tales:
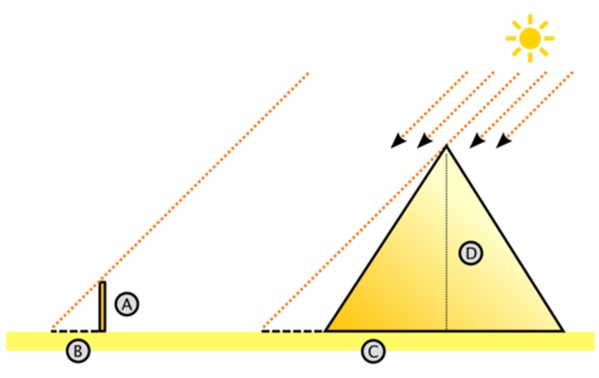
Tales supuso acertadamente que los rayos del Sol inciden paralelamente. Con esto en mente, imaginó el triángulo rectángulo grande de la derecha.
Allí D es la altura de la pirámide y C es la distancia sobre el suelo medida desde el centro hasta la sombra proyectada por la pirámide sobre el suelo del desierto. Puede que sea trabajoso medir C, pero sin duda es más fácil que medir la altura de la pirámide.
A la izquierda está el triángulo pequeño, de catetos A y B, donde A es la altura de la estaca clavada verticalmente en el suelo y B es la sombra que proyecta. Ambas longitudes son medibles, al igual que C (C es igual a la longitud de la sombra + la mitad del largo de la pirámide).
Entonces, por semejanza de triángulos:
A/B = D/C
Y la altura de la Gran Pirámide resulta ser: D = C.(A/B)
Las armaduras en construcción civil son estructuras a base de barras delgadas rectas de madera o de metal entrecruzadas, que se utilizan como soporte en muchos edificios. También se las conoce como celosías, cerchas o reticulados (truss en inglés).
En ellas los triángulos están siempre presentes, pues las barras van interconectadas en puntos llamados nodos, que pueden estar fijos o articulados.

El método conocido como triangulación permite obtener la ubicación de puntos inaccesibles conociendo otras distancias más fáciles de medir, a condición de que se forme un triángulo que incluya entre sus vértices la localización deseada.
Por ejemplo, en la siguiente figura se quiere saber en qué punto del mar está el barco, denotado como B.
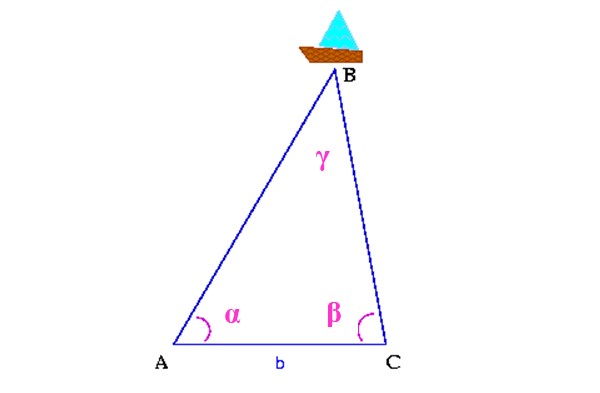
En primer lugar se mide la distancia entre dos puntos sobre la costa, que en la figura son A y C. Enseguida hay que determinar los ángulos α y β, con ayuda de un teodolito, un aparato que sirve para medir ángulos verticales y horizontales.
Con toda esta información se construye un triángulo en cuyo vértice superior está el barco. Restaría calcular el ángulo γ, mediante las propiedades de los triángulos y las distancias AB y CB mediante la trigonometría, para determinar la posición del barco en el mar.
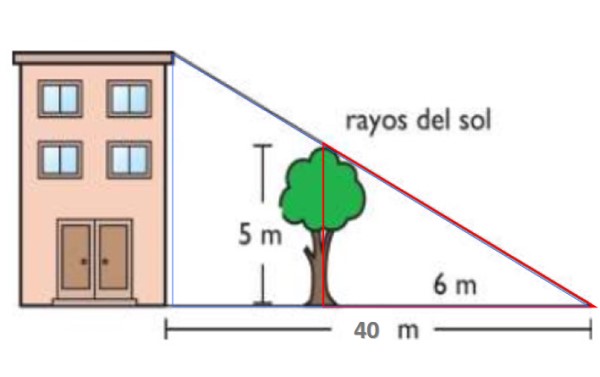
En la figura mostrada, los rayos del sol son paralelos. De esta forma el árbol de 5 metros de altura proyecta una sombra de 6 metros sobre el suelo. A esa misma hora, la sombra del edificio es de 40 metros. Siguiendo el primer teorema de Tales, encuentre la altura del edificio.
Solución
El triángulo rojo tiene lados de 5 y 6 metros respectivamente, mientras que el azul tiene altura H –la altura del edificio- y base 40 metros. Ambos triángulos son semejantes, por lo tanto:
H/ 40 = 5 /6 → H= 40.(5/6) m = 33.3 m
Se necesita conocer la distancia horizontal entre dos puntos A y B, pero están situados sobre un terreno muy irregular.
Aproximadamente en el punto medio (Pm) de dicho terreno sobresale una prominencia de 1.75 metros de altura. Si la cinta métrica indica 26 metros de longitud medidos desde A hasta la prominencia, y 27 metros desde B hasta el mismo punto, encuentre la distancia AB.
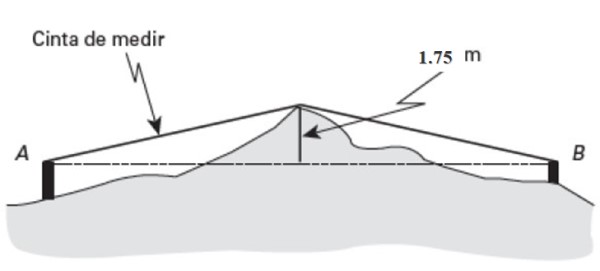
Solución
Se aplica el teorema de Pitágoras a uno de los dos triángulos rectángulos de la figura. Comenzando por el de la izquierda:
Hipotenusa= c= 26 metros
Altura = a = 1.75 metros
APm = (262 – 1.752)1/2 = 25.94 m
Ahora se aplica Pitágoras en el triángulo de la derecha, esta vez c =27 metros, a = 1.75 metros. Con estos valores:
BPm=(272 – 1.752)1/2 = 26.94 m
La distancia AB se encuentra sumando estos resultados:
AB = 25.94 m + 26.94 m = 52.88 m.
- Baldor, J. A. 1973.Geometría plana y del espacio. Cultural centroamericana.
- Barredo, D. La geometría del triángulo. Recuperado de: ficus.pntic.mec.es.
- Jiménez, R. 2010. Matemáticas II. Geometría y Trigonometría. Segunda Edición. Pearson.
- Wentworth, G. Plane Geometry. Recuperado de: gutenberg.org.
- Wikipedia. Triángulo. Recuperado de: es. wikipedia.org.
