Vector equilibrante: cálculo, ejemplos, ejercicios
El vector equilibrante es aquel que se contrapone al vector resultante y por ende es capaz de equilibrar a un sistema, ya que tiene la misma magnitud y la misma dirección, pero sentido contrario a este.
En numerosas ocasiones el vector equilibrante se refiere a un vector de fuerza. Para calcular la fuerza equilibrante primero se encuentra la fuerza resultante, tal y como se muestra en la siguiente figura:
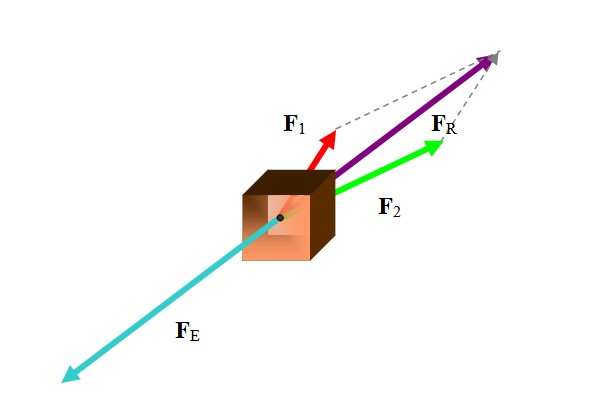
Hay diversos métodos para emprender esta tarea, según los datos que se tengan a la mano. Como las fuerzas son vectores, la resultante es la suma vectorial de las fuerzas participantes:
FR = F1 + F2 + F3 + ….
Entre los métodos a utilizar están los métodos gráficos como el la poligonal, el del paralelogramo y los métodos analíticos como la descomposición de fuerzas en sus componentes cartesianas. En el ejemplo la figura se empleó el método del paralelogramo.
Una vez hallada la fuerza resultante, la fuerza equilibrante es justamente el vector opuesto.
Si FE es la fuerza equilibrante, entonces se cumple que FE aplicada en cierto punto, garantiza el equilibrio de traslación del sistema. Si se trata de una sola partícula, esta no se moverá (o tal vez lo haga con velocidad constante), pero si se trata de un objeto extendido, aún tendrá la posibilidad de girar:
FR + FE = 0
Índice del artículo
Las fuerzas equilibrantes están presentes en todas lados. Nosotros mismos nos encontramos equilibrados por la fuerza que la silla ejerce para compensar el peso. Los objetos que se encuentran en reposo: libros, muebles, lámparas de techo y gran cantidad de mecanismos, están siendo equilibrados continuamente por fuerzas.
Por ejemplo un libro en reposo sobre una mesa es equilibrado por la fuerza normal que aquella ejerce sobre el libro, impidiéndole caer. Lo mismo sucede con la cadena o el cable que sujeta la lámpara que pende del techo en una sala. Los cables que sujetan una carga se reparten su peso a través de la tensión en ellos.
En un fluido algunos objetos son capaces de flotar y permanecer en reposo, ya que su peso es equilibrado por una fuerza ascendente ejercida por el líquido, denominada empuje.
Diversos mecanismos requieren ser equilibrados conociendo el vector fuerza equilibrante tales como barras, vigas y columnas.
Al momento de usar una balanza, es necesario equilibrar de alguna manera el peso del objeto con una fuerza que sea equivalente, ya sea agregando pesas o mediante resortes.
La mesa de fuerzas se utiliza en el laboratorio para determinar la fuerza equilibrante. Consiste en una plataforma circular, de la cual se tiene la vista superior en la figura, y que dispone de transportador para medir ángulos.
En los bordes de la mesa hay poleas por las que pasan cuerdas que sujetan pesas y que confluyen en un aro que está en el centro.
Por ejemplo se cuelgan dos pesas. Las tensiones generadas en las cuerdas por estas pesas están dibujadas en rojo y azul en la figura 2. Una tercera pesa en verde, puede equilibrar la fuerza resultante de las otras dos y mantener el sistema en equilibrio.
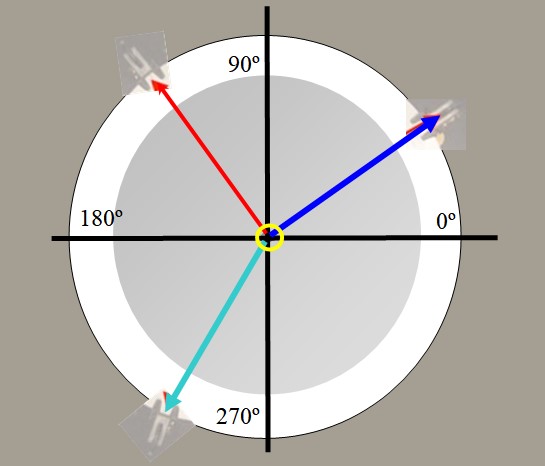
Con la mesa de fuerzas se puede verificar el carácter vectorial de las fuerzas, descomponer fuerzas, encontrar la fuerza equilibrante y verificar el teorema de Lamy:
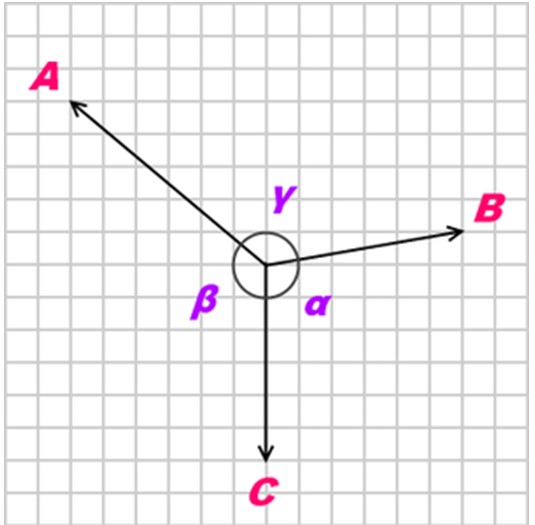
Si un cuerpo se encuentra en equilibrio gracias a tres fuerzas coplanares, concurrentes y no colineales (no paralelas), denominadas A, B y C, la relación entre dichas fuerzas es la siguiente:
A/ sen α= B / sen β = C/sen γ
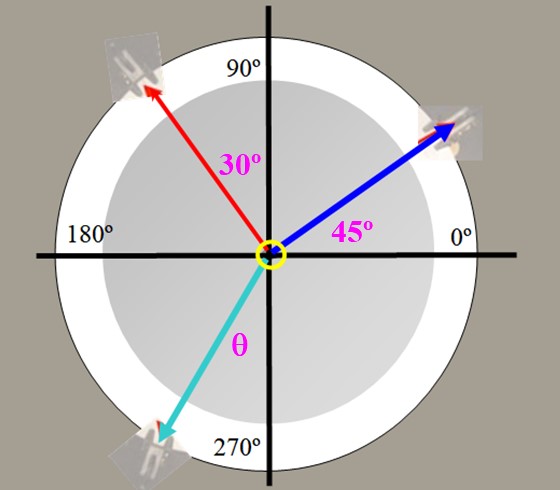
En la mesa de fuerzas de la figura 2 se cuelgan pesas de 225 g (tensión azul) y 150 g (tensión en rojo), con los ángulos mostrados. Encontrar el valor de la fuerza equilibrante y el ángulo que esta forma con el eje vertical.
Solución
El problema se puede trabajar con los pesos expresados en gramos (fuerzas). Sea P1 = 150 gramos y P2 = 225 gramos, los respectivas componentes de cada uno son:
P1x = 225 . cos 45º g = 159.10 g ; P1y = 225 . cos 45º g = 159.10 g
P2x = -150 . sen 30º g= -75.00 g ; P2y = 150 . cos 30º g = 129.90 g
El peso resultante PR se encuentra sumando algebraicamente las componentes:
PRx = 159.10 – 75.00 g = 84.10 g
PRy = 159.10 + 129.90 g = 289.00 g
El peso equilibrante PE es el vector opuesto a PR:
PEx = -84.10 g
PEy = -289.00 g
La magnitud del peso equilibrante se calcula mediante:
PE = (PEx2 + PEy2)1/2 = ((-84.10)2 + (-289.00)2)1/2 g = 301 g
El ángulo θ de la figura es:
θ = arctg (-84.10 / -289.00) = 16.2 º respecto al eje y negativo.
Encontrar el vector equilibrante del sistema mostrado en la figura, sabiendo que cada cuadrado mide 10 m de lado.
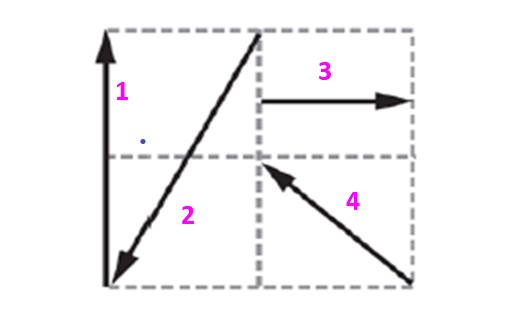
Solución
Los vectores contenidos en esta cuadrícula serán expresados en términos de los vectores unitarios y ortogonales i y j que determinan el plano. El vector 1, al que se denotará como v1 tiene magnitud 20 m y está dirigido verticalmente hacia arriba. Se puede expresar como:
v1 = 0 i +20 j m
Del dibujo se observa que el vector 2 es:
v2 = -10 i – 20 j m
El vector 3 es horizontal y apunta en la dirección positiva:
v3 = 10 i + 0 j m
Finalmente el vector 4 está inclinado 45 º, ya que es la diagonal del cuadrado, por lo tanto sus componentes miden lo mismo:
v4 = -10 i + 10 j m
Obsérvese que los signos señalan hacia qué lado del eje están las componentes: arriba y a la derecha tiene signo +, mientras que abajo y a la izquierda tienen signo -.
El vector resultante se obtiene sumando componente a componente:
vR = -10 i + 10 j m
Luego el vector equilibrante del sistema es:
vE = 10 i – 10 j m
- Beardon, T. 2011. An introduction to vectors. Recobrado de: nrich.maths.org.
- Bedford, 2000. A. Mecánica para Ingeniería: Estática. Addison Wesley. 38-52.
- Figueroa, D. Serie: Física para Ciencias e Ingeniería. Volumen 1. Cinemática.31-68.
- Física. Módulo 8: Vectores. Recobrado de: frtl.utn.edu.ar
- Hibbeler, R. 2006. Mecánica para Ingenieros. Estática. 6ta Edición. Compañía Editorial Continental. 15-53.
- Vector Addition Calculator. Recobrado de: 1728.org
- Vectores. Recobrado de: wikibooks.org
