Inducción magnética: fórmulas, cómo se calcula y ejemplos
La inducción magnética o densidad de flujo magnético es una alteración del entorno causada por la presencia de corrientes eléctricas. Ellas modifican la naturaleza del espacio que las rodea, creando un campo vectorial.
El vector inducción magnética, densidad de flujo magnético o simplemente campo magnético B, posee tres características distintivas: una intensidad expresada por un valor numérico, una dirección y además un sentido dados en cada punto del espacio. Se resalta en negrita para distinguirlo de las cantidades puramente numéricas o escalares.
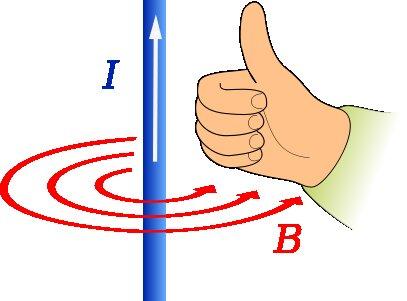
La regla del pulgar derecho se utiliza para encontrar la dirección y el sentido del campo magnético originado por un alambre que transporta corriente, tal como se muestra en la figura de arriba.
El pulgar de la mano derecha debe apuntar en la dirección de la corriente. Entonces el giro de los cuatro dedos restantes indica la forma de B, que en la figura está representada por los círculos concéntricos de color rojo.
En tal caso, la dirección de B es tangencial a la circunferencia concéntrica con el alambre y el sentido es contrario a las manecillas del reloj.
La inducción magnéticaBen el Sistema Internacional se mide Tesla (T), sin embargo es más frecuente medirla en otra unidad llamada Gauss (G). Ambas unidades fueron nombradas respectivamente en honor a Nikola Tesla (1856-1943) y Carl Friedrich Gauss (1777-1855) por sus extraordinarios aportes a la ciencia de la electricidad y el magnetismo.
Índice del artículo
- 1 ¿Cuáles son las propiedades de la inducción magnética o densidad de flujo magnético?
- 2 La ley de Biot-Savart
- 3 Fórmulas
- 4 ¿Cómo se calcula?
- 5 Referencias
Una brújula que se coloque cerca del alambre con corriente, se alineará siempre con B. El físico danés Hans Christian Oersted (1777-1851) fue el primero en percatarse de este fenómeno a comienzos del siglo XIX.
Y cuando la corriente cesa, la brújula vuelve a apuntar al norte geográfico, como siempre. Al ir cambiando cuidadosamente la posición de la brújula, se obtiene un mapa de la forma del campo magnético.
Este mapa tiene siempre la forma de círculos concéntricos al alambre, tal como se describió al comienzo. De esta forma se puede visualizar B.
Aún si el alambre no es recto, el vector B formará círculos concéntricos a su alrededor. Para determinar que forma tiene el campo, basta con imaginar segmentos muy pequeños de alambre, tan pequeños que parezcan rectilíneos y rodeados de circunferencias concéntricas.

Esto señala una propiedad importante de las líneas del campo magnético B: carecen de principio o fin, siempre son curvas cerradas.
El siglo XIX determinó el comienzo de la era de la Electricidad y el Magnetismo en la ciencia. Cerca del año 1820 los físicos franceses Jean Marie Biot (1774-1862) y Felix Savart (1791-1841) descubrieron la ley que lleva su nombre y que permite calcular el vector B.
Ellos realizaron las siguientes observaciones acerca de la contribución al campo magnético producido por un segmento de alambre de longitud diferencial dl que transporta una corriente eléctrica I:
- La magnitud de B decrece con el inverso al cuadrado de la distancia al alambre (esto tiene sentido: lejos del alambre la intensidad de B debe ser menor que en puntos cercanos).
- La magnitud de B es proporcional a la intensidad de la corriente I que transita por el alambre.
- La dirección de B es tangencial a la circunferencia de radio r centrada en el alambre y el sentido de B viene dado, como dijimos, por la regla del pulgar derecho.
El producto vectorial o producto cruz es la herramienta matemática apropiada para expresar el último punto. Para establecer un producto vectorial hacen falta dos vectores, los cuales se definen así:
- dl es el vector cuya magnitud es la longitud del segmento diferencial dl
- r es el vector que va desde el alambre hasta el punto donde se desea encontrar el campo
Todo esto puede combinarse en una expresión matemática:
La constante de proporcionalidad necesaria para establecer la igualdad es la permeabilidad magnética del espacio libre μo = 4π.10-7 T.m/A
Esta expresión es la ley de Biot y Savart, que permite calcular el campo magnético de un segmento de corriente.
Tal segmento a su vez debe formar parte de un circuito más grande y cerrado: una distribución de corriente.
La condición de que el circuito sea cerrado es necesaria para que fluya una corriente eléctrica. La corriente eléctrica no puede fluir en circuitos abiertos.
Finalmente, para encontrar el campo magnético total de dicha distribución de corriente, se suman todas las contribuciones de cada segmento diferencial dl. Esto equivale a integrar sobre toda la distribución:
Para aplicar la ley de Biot-Savart y calcular el vector inducción magnética, es necesario considerar unos puntos importantes muy importantes:
- El producto vectorial entre dos vectores siempre tiene como resultado otro vector.
- Conviene hallar el producto vectorial antes de pasar a la resolución de la integral, luego se resuelve la integral de cada una de las componentes obtenidas por separado.
- Es necesario hacer un dibujo de la situación y establecer un sistema de coordenadas adecuado.
- Siempre que se observe la existencia de alguna simetría, se debe aprovechar para ahorrar tiempo de cálculo.
- Cuando existan triángulos, el teorema de Pitágoras y el teorema del coseno son de gran ayuda para establecer la relación geométrica entre las variables.
Con un ejemplo práctico del cálculo de Bpara un alambre rectilíneo, se aplican estas recomendaciones.
Calcule el vector campo magnético que un alambre rectilíneo muy largo, produce en un punto P del espacio, según la figura mostrada.
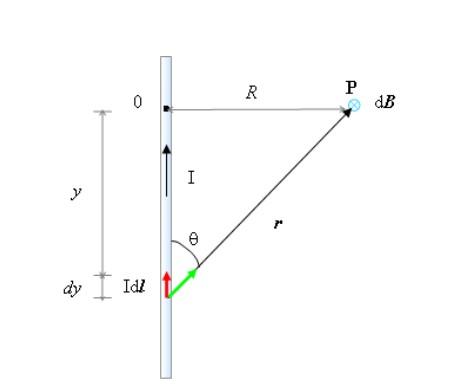
A partir de la figura se tiene que:
- El alambre se encuentra dirigido en dirección vertical, con la corriente I fluyendo hacia arriba. Esta dirección es +y en el sistema de coordenadas, cuyo origen está en el punto O.
- En tal caso, de acuerdo a la regla del pulgar derecho, B en el punto P va dirigido hacia dentro del papel, por eso se denota con un pequeño círculo y una “x” en la figura. Esta dirección se tomará como -z.
- El triángulo rectángulo cuyos catetos son y y R, relaciona ambas variables según el teorema de Pitágoras: r2=R2+y2
Se sustituye todo esto en la integral. El producto vectorial o cruz se indica mediante su magnitud más su dirección y su sentido:
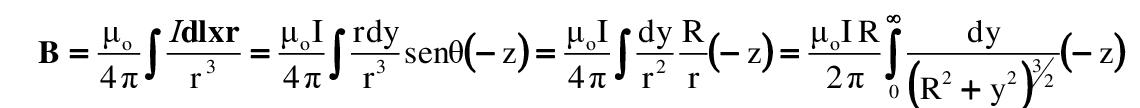
La integral planteada se busca en una tabla de integrales o se resuelve mediante una sustitución trigonométrica apropiada (el lector puede comprobar el resultado usando y = Rtg θ):
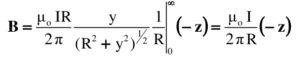
El resultado concuerda con lo esperado: la magnitud del campo decrece con la distancia R y aumenta proporcionalmente con la intensidad de la corriente I.
Si bien un alambre infinitamente largo es una idealización, la expresión obtenida es una muy buena aproximación para el campo de un alambre largo.
Con la ley de Biot y Savart es posible encontrar el campo magnético de otras distribuciones de alta simetría, tal como una espira circular que transporta corriente, o bien alambres doblados combinando segmentos rectilíneos y curvilíneos.
Desde luego que para resolver analíticamente la integral planteada, el problema deberá tener un alto grado de simetría. De lo contrario la alternativa es solucionar numéricamente la integral.
- Serway, R., Jewett, J. (2008). Física para Ciencias e Ingeniería. Volumen 2. México. Cengage Learning Editores. 367-372.
