Ley de Coulomb: explicación, fórmula y unidades, ejercicios, experimentos
La ley de Coulomb es la ley física que rige la interacción entre objetos cargados eléctricamente. Fue enunciada por el científico francés Charles Augustin de Coulomb (1736-1806), gracias a los resultados de sus experimentos mediante la balanza de torsión.
En 1785, Coulomb experimentó innumerables veces con pequeñas esferas cargadas eléctricamente, por ejemplo acercando o alejando dos esferas, variando la magnitud de su la carga y también su signo. Siempre observando y registrando cuidadosamente cada respuesta.
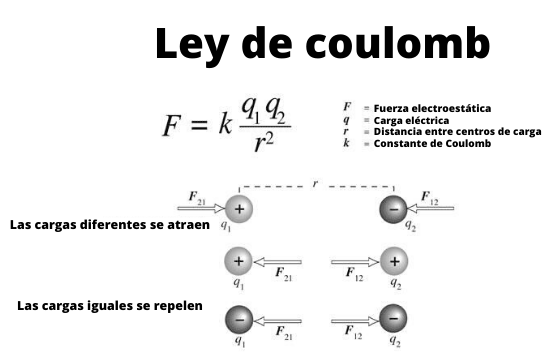
Estas pequeñas esferas pueden considerarse como cargas puntuales, es decir, objetos cuyas dimensiones son insignificantes. Y ellas cumplen, como se sabe desde la época de los antiguos griegos, que las cargas de igual signo se repelen y las de distinto signo se atraen.

Con esto en mente, Charles Coulomb encontró lo siguiente:
-La fuerza de atracción o repulsión entre dos cargas puntuales es directamente proporcional al producto de la magnitud de las cargas.
-Dicha fuerza siempre está dirigida a lo largo de la línea que une las cargas.
-Finalmente, la magnitud de la fuerza es inversamente proporcional al cuadrado de la distancia que separa las cargas.
Índice del artículo
- 1 Fórmula y unidades de la ley de Coulomb
- 2 Cómo aplicar la ley de Coulomb
- 3 Ejercicios resueltos
- 4 Experimentos
- 5 Referencias
Gracias a estas observaciones, Coulomb concluyó que la magnitud de la fuerza F entre dos cargas puntuales q1 y q2, separadas una distancia r, viene dada matemáticamente como:
Como la fuerza es una magnitud vectorial, para expresarla completamente se define un vector unitario ren la dirección de la línea que une las cargas (un vector unitario tiene magnitud igual a 1).
Adicionalmente, la constante de proporcionalidad necesaria par transformar la expresión anterior en una igualdad se denomina ke o simplemente k: la constante electrostática o constante de Coulomb.
Finalmente se establece la ley de Coulomb para cargas puntuales, dada por:
La fuerza, como siempre en el Sistema Internacional de Unidades, viene en newton (N). En cuanto a las cargas, la unidad recibe el nombre de coulomb (C) en honor a Charles Coulomb y por último la distancia r viene en metros (m).
Observando atentamente la ecuación anterior, es claro que la constante electrostática debe tener unidades de N.m2 / C2, para obtener newtons como resultado. El valor de la constante se determinó experimentalmente como:
ke = 8.89 x 10 9 N.m2 / C2 ≈ 9 x 10 9 N.m2 / C2
La figura 1 ilustra la interacción entre dos cargas eléctricas: cuando son del mismo signo se repelen, de lo contrario se atraen.
Nótese que la ley de Coulomb se ajusta a la tercera ley de Newton o ley de acción y reacción, por lo tanto las magnitudes de F1 y F2 son iguales, la dirección es la misma, pero los sentidos son contrarios.
Para resolver problemas de interacciones entre cargas eléctricas, hay que tener en cuenta lo siguiente:
– La ecuación se aplica exclusivamente en el caso de cargas puntuales, es decir, objetos cargados eléctricamente pero de dimensiones muy pequeñas. Si los objetos cargados tienen dimensiones mensurables, es necesario dividirlos en cargas muy pequeñas y luego sumar las contribuciones de cada una de estas cargas, para lo cual se requiere de cálculo integral.
– La fuerza eléctrica es una magnitud vectorial. Si hay más de dos cargas interactuando, la fuerza neta sobre la carga qi viene dada por el principio de superposición:
Fneta = Fi1 + Fi2 + Fi3 + Fi4 + … = ∑ Fij
Donde el subíndice j vale 1, 2, 3, 4… y representa a cada una de las restantes cargas.
– Siempre se debe ser consistente con las unidades. Lo más frecuente es trabajar con la constante electrostática en unidades SI, entonces hay que asegurarse de que las cargas estén en coulomb y las distancias en metros.
– Por último, la ecuación se aplica cuando las cargas están en equilibrio estático.
En la siguiente figura hay dos cargas puntuales +q y +2q. Una tercera carga puntual –q se coloca en P. Se pide encontrar la fuerza eléctrica sobre esta carga debido a la presencia de las otras.
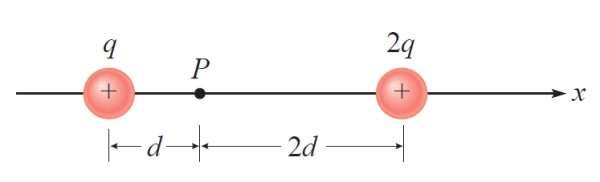
Solución
Lo primero es establecer un sistema de referencia adecuado, que en este caso es el eje horizontal o eje x. El origen de dicho sistema puede estar en cualquier lugar, pero por comodidad se colocará en P, como se muestra en la figura 4a:
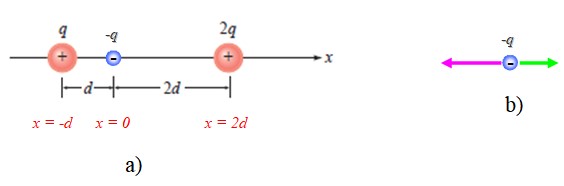
También se muestra un esquema de las fuerzas sobre –q, tomando en cuenta que es atraída por las otras dos (figura 4b).
Llamemos F1 a la fuerza que ejerce la carga q sobre la carga –q, están dirigida a lo largo del eje x y apunta en el sentido negativo, por lo tanto:
De forma análoga se calcula F2:
Nótese que la magnitud de F2 es la mitad de la de F1, aunque la carga es el doble. Para encontrar la fuerza neta, finalmente se suman vectorialmente F1 y F2:
Fneta = (-k + k/2).(q2 /d2) (x) N = – (k/2).(q2 /d2) (x) N
Dos esferitas de poliestireno de igual masa m = 9.0 x 10-8 kg tienen igual carga positiva Q y están suspendidas mediante un hilo de seda de longitud L = 0,98 m. Las esferas están separadas una distancia de d = 2 cm. Calcular el valor de Q.
Solución
La situación del enunciado se describe en la figura 5a.
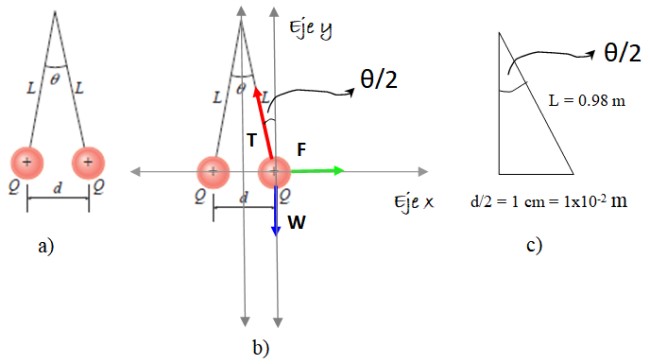
Elegimos una de las esferitas y sobre ella dibujamos el diagrama de cuerpo aislado, que incluye tres fuerzas: pesoW, tensión en la cuerda T y repulsión electrostática F, tal como aparece en la figura 5b. Y ahora los pasos:
Paso 1
Se calcula el valor de θ/2 con el triángulo de la figura 5c:
θ/2 = arcsen (1 x 10-2/0.98 ) = 0.585º
Paso 2
Seguidamente hay que aplicar la segunda ley de Newton e igualar a 0, ya que las cargas están en equilibrio estático. Es importante destacar que la tensión T está inclinada y tiene dos componentes:
∑Fx = -T.sen θ + F = 0
∑Fy = T.cos θ – W = 0
Paso 3
Despejamos la magnitud de la tensión de la última ecuación:
T = W/ cos θ = mg/ cos θ
Paso 4
Este valor se sustituye en la primera ecuación para hallar la magnitud de F:
F = T sen θ = mg (sen θ / cos θ) = mg. tg θ
Paso 5
Como F = k Q2 /d2, se despeja Q:
Q = 2×10-11 C.
Comprobar la ley de Coulomb es sencillo mediante una balanza de torsión semejante a la que usó Coulomb en su laboratorio.
Se dispone de dos pequeñas esferas de saúco, una de las cuales, la que está en el centro de la balanza, está suspendida de un hilo. El experimento consiste en tocar las esferas de saúco descargadas con otra esfera metálica cargada con carga Q.

Inmediatamente la carga se reparte por igual entre las dos esferas de saúco, pero entonces, como son cargas del mismo signo, se repelen. Sobre la esfera suspendida actúa una fuerza que causa la torsión del hilo del que pende y se aleja inmediatamente de la esfera fija.
Después vemos que oscila unas cuantas veces hasta que alcanza el equilibrio. Entonces la torsión de la barra o hilo que la sujeta es equilibrada por la fuerza de repulsión electrostática.
Si originalmente las esferas estaban a 0º, ahora la esfera móvil habrá girado un ángulo θ. Circundando la balanza, hay una cinta graduada en grados para medir este ángulo. Al determinar previamente la constante de torsión, entonces la fuerza de repulsión y el valor de la carga adquirida por las esferas de saúco se calcula fácilmente.
- Figueroa, D. 2005. Serie: Física para Ciencias e Ingeniería. Volumen 5. Electrostática. Editado por Douglas Figueroa (USB).
- Giambattista, A. 2010. Physics. Second Edition. McGraw Hill.
- Giancoli, D. 2006. Physics: Principles with Applications. 6th. Ed Prentice Hall.
- Resnick, R. 1999. Física. Vol. 2. 3ra Ed. en español. Compañía Editorial Continental S.A. de C.V.
- Sears, Zemansky. 2016. University Physics with Modern Physics. 14th. Ed. Volume 2.
