Razón de cambio: qué es, cómo se calcula, ejemplos, ejercicios

¿Qué es la razón de cambio?

La razón de cambio es la magnitud matemática que define el cambio de una variable o de una magnitud física respecto de otra. Por ejemplo, la velocidad es la razón de cambio de la posición respecto del tiempo.

Un cambio en una magnitud x, se denota con la letra griega Δ (se lee “delta”) y se escribe Δx. Se calcula mediante la diferencia entre un valor final y otro inicial: Δx= x_final− x_inicial.

Si la magnitud x está relacionada con otra magnitud y, esta también experimenta un cambio, llamado Δy= y_final− y_inicial, la razón de cambio de y con respecto a x se define como el cociente:

La cual, empleando la notación con delta indicada antes, queda así:

Este cociente se conoce como el cociente de incremento de y con respecto a x o razón de cambio media o promedio.

De esta forma se pueden definir magnitudes como el índice de crecimiento de una población, velocidad con la que se mueve un objeto, tasa de desempleo, el caudal del agua a través de una tubería y muchas más. Todas estas cantidades son, en efecto, razones de cambio.

¿Por qué es importante calcular la razón de cambio?

Numerosas magnitudes de interés no permanecen inmutables, sino que experimentan cambios, y con frecuencia estos cambios se suceden en el tiempo. De allí la importancia de calcular la razón de cambio de una magnitud en el tiempo.

Por ejemplo, está el caso sencillo de un objeto que se desplaza a lo largo de una línea recta, que puede ser el eje horizontal o eje de las x. El móvil (un auto, una bicicleta, una persona que camina o corre…) cambia continuamente su posición al pasar el tiempo t.

Entonces, a la razón de cambio de la posición del objeto Δx en el intervalo de tiempo Δt, se le conoce como velocidad media:

Otro móvil que transite por esa misma línea recta puede hacerlo con diferente velocidad, sea mayor o menor, y de esta forma se distingue del primer móvil (por ser más lento o más rápido).

Por ejemplo, un corredor de 100 metros planos tendrá una tasa de cambio promedio en su posición mucho mayor que un maratonista o una persona que camina tranquilamente por la calle.

La velocidad es un ejemplo típico de razón de cambio, pero algunas magnitudes interesantes que también experimentan cambios en el tiempo, son: la temperatura, el volumen de un fluido, la carga eléctrica, una población de bacterias y muchas más.

Conociendo su razón de cambio, se puede saber mucho acerca de la forma en que estas magnitudes evolucionan en el tiempo.

Unidades de la razón de cambio

Siendo la razón de cambio el cociente entre dos magnitudes, las unidades resultantes serán asimismo el cociente de las unidades empleadas para medirlas. Por ejemplo, la velocidad es longitud entre tiempo, ya que es la razón de cambio de la posición respecto al tiempo.

De esta forma, las unidades de la velocidad pueden ser metros/segundo, kilómetros/hora, millas/hora y muchas otras combinaciones más.

¿Cómo se calcula la razón de cambio?

La razón o tasa de cambio promedio entre dos magnitudes se calcula fácilmente, al efectuar el cociente entre las respectivas variaciones de cada una, según la fórmula:

Los cambios en las magnitudes pueden venir dados a través de tablas de valores o ser determinados mediante una gráfica, de la cual se toman los respectivos valores de y y x (ver los ejercicios resueltos al final).

Por otro lado:

Y la expresión de la derecha es precisamente la pendiente de una recta, de lo cual se concluye que la razón de cambio promedio es la pendiente de la recta secante a la gráfica de Y en función de x.

Signos de la razón de cambio

De acuerdo a la definición dada, la razón de cambio puede ser positiva o negativa, según cómo varían las magnitudes involucradas, ya que estas pueden aumentar o disminuir, según.

Si la razón de cambio es positiva, significa que los cambios en y y en x fueron del mismo signo, es decir, y aumentó y x también lo hizo. O bien tanto y como x disminuyeron.

Sin embargo, cuando la razón de cambio es negativa, significa que una de las magnitudes aumentó y la otra disminuyó.

Razón de cambio instantánea

Con frecuencia, es mucho más interesante calcular la razón de cambio instantánea en vez del cociente de incrementos. En tal caso, es preciso hacer que la variación Δx se haga sumamente pequeña, tendiendo a 0 (pero sin llegar a ser 0, pues la división entre 0 no está definida).

A esto se le llama “tomar el límite”, y en tal caso, la razón de cambio instantánea pasa a llamarse la “derivada” de y con respecto de x y se denota como dy/dx; así:

La razón o tasa de cambio instantánea también equivale a la pendiente de una recta, pero en este caso es la pendiente de la recta tangente a la gráfica de y versus x.

Ejemplos sencillos

El crecimiento de una persona

Desde que nacen, los niños crecen a un ritmo determinado por varios factores, entre los cuales destacan la genética y la alimentación. Las tasas de crecimiento más elevadas se producen durante el primer año de vida; más tarde, durante la niñez y luego en la pubertad, los niños normalmente experimentan “estirones”, es decir, la razón de cambio de la estatura respecto al tiempo aumenta, para luego disminuir.

Posterior a la pubertad, los chicos siguen creciendo, pero la tasa disminuye hasta anularse, una vez que alcanzan su estatura definitiva de adultos.

Enfriamiento del café

Es un hecho conocido que el café o la sopa caliente se enfrían paulatinamente cuando se dejan a temperatura ambiente. Sin embargo, la tasa de enfriamiento se ralentiza cuanto más se acerca la temperatura del café o la sopa a la temperatura ambiente.

Una forma de modelar este fenómeno es a través de la ley de enfriamiento de Newton, según la cual, la tasa a la que se transfiere el calor Q es proporcional a la diferencia entre la temperatura de la sustancia y la temperatura ambiente. La constante de proporcionalidad k es característica de la sustancia:

T_o representa la temperatura del medio ambiente.

Ejercicios resueltos

Ejercicio 1

Calcular la razón de cambio promedio de y con respecto a x, dados los siguientes valores:

y₁ = 3; y₂ = 10; x₁ = 2; x₂ = 5

Solución

De acuerdo a la fórmula:

Se sustituyen los valores dados en el enunciado y se resuelve la operación:

La gráfica muestra las respectivas curvas de distancia versus tiempo de dos patinadores olímpicos de velocidad A y B, en la modalidad de 500 metros. ¿Quién ganó la carrera? ¿Cuál fue la velocidad promedio de cada patinador?

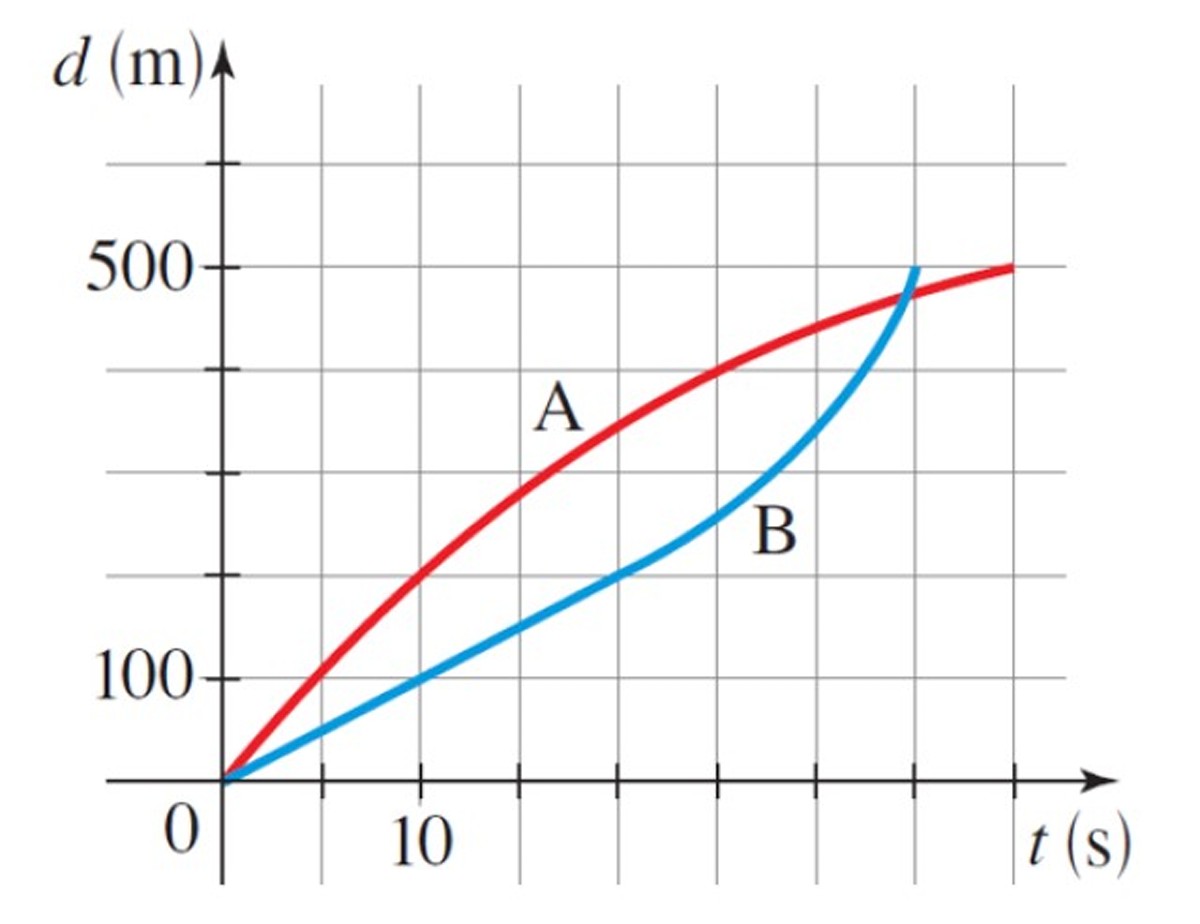
Solución

Observando la gráfica, se deduce que el patinador B (curva azul) ganó la carrera, ya que recorrió los 500 m en 35 s, mientras que el patinador A (curva roja), lo hizo en 40 s.

Las respectivas velocidades medias fueron:

Referencias

1. Figueroa, D. (2005). Serie: Física para Ciencias e Ingeniería. Volumen 1. Cinemática. Editado por Douglas Figueroa (USB).
2. Glencoe Science. Rate of Change and Slope (2021). Recuperado de: glencoe.com.
3. Larson, R. (2012). Precálculo. 8va. Edición. Cengage Learning.
4. Larson, R. (1986). Cálculo con Geometría Analítica, 2da. Edición. McGraw-Hill.
5. Stewart, J. (2011). College Algebra, Concepts and Contexts. Brooks/Cole.