Teoría cinética molecular: historia, postulados y ejemplos
La teoría cinética molecular es aquella que busca explicar las observaciones experimentales de los gases desde una perspectiva microscópica. Es decir, intenta asociar la naturaleza y comportamiento de las partículas gaseosas, con las características físicas del gas como fluido; explicar lo macroscópico a partir de lo microscópico.
Los gases siempre han sido objeto de interés para los científicos debido a sus propiedades. Ocupan todo el volumen del recipiente en el que se encuentran, pudiéndose comprimir completamente sin que su contenido oponga la menor resistencia; y si aumenta la temperatura, el recipiente comienza a expandirse, e incluso, puede llegar a agrietarse.
Muchas de estas propiedades y comportamientos se resumen en las leyes de los gases ideales. Sin embargo, consideran el gas como un todo y no como un conjunto de millones de partículas dispersas en el espacio; además, no proporciona, a partir de datos de presión, volumen y temperatura, mayor información respecto a cómo se desplazan estas partículas.
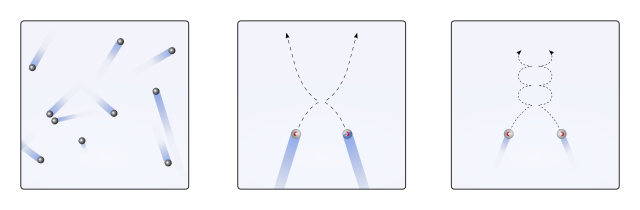
Es así entonces que la teoría cinética molecular (TCM), plantea visualizarlas como esferas móviles (imagen superior). Estas esferas colisionan entre sí y las paredes de manera arbitraria, y mantienen una trayectoria lineal. No obstante, cuando disminuye la temperatura y aumenta la presión, la trayectoria de las esferas se torna curva.
Un gas, de acuerdo a la TCM, debe comportarse como las esferas del primer recuadro de la imagen. Pero, al enfriarse y aumentar la presión sobre ellas, su comportamiento se aleja del ideal. Se tratan entonces de gases reales, próximos a sufrir licuefacción y pasar por ende a la fase líquida.
En estas condiciones, las interacciones entre las esferas cobran mayor importancia, a tal punto que enlentecen momentáneamente sus velocidades. Cuanto más cerca estén de la licuefacción, más curvas se tornan sus trayectorias (recuadro de la derecha), y sus colisiones son menos energéticas.
Índice del artículo
- 1 Historia
- 2 Postulados de la teoría cinética molecular
- 2.1 El volumen de las partículas gaseosas es despreciable
- 2.2 Las fuerzas de atracción entre las partículas son nulas
- 2.3 Las partículas gaseosas siempre están en movimiento
- 2.4 Las colisiones entre las partículas y las paredes del recipiente son elásticas
- 2.5 La energía cinética no permanece constante
- 2.6 La energía cinética promedio es igual a una temperatura dada para todos los gases
- 3 Ejemplos
- 4 Referencias
La idea de estas esferas, mejor llamadas átomos, ya había sido considerada por el filósofo romano Lucretius; no para los gases, sino para objetos macizos, estáticos. Por otra parte, en 1738 Daniel Bernoulli aplicó la visión atómica a los gases y líquidos al imaginarlos como esferas desordenadas moviéndose en todas direcciones.
Su trabajo, no obstante, violaba las leyes de la física por aquel entonces; un cuerpo no podía moverse eternamente, por lo que resultaba imposible pensar que un conjunto de átomos y moléculas colisionaran entre ellas sin pérdida de su energía; esto es, no era posible la existencia de las colisiones elásticas.
Un siglo después, otros autores reforzaron la TCM con un modelo donde las partículas gaseosas se trasladaban en una sola dirección. Rudolf Clausius, no obstante, recopiló sus resultados y armó un modelo más completo de la TCM con el cual buscó explicar las leyes de los gases ideales demostradas por Boyle, Charles, Dalton y Avogadro.
En 1859, James Clerk Maxwell planteó que las partículas gaseosas exhiben un rango de velocidades a una temperatura dada, y que un conjunto de las mismas puede considerarse mediante una velocidad molecular promedio.
Luego, en 1871 Ludwig Boltzmann conectó las ideas existentes con la entropía, y cómo el gas termodinámicamente siempre tiende a ocupar el máximo espacio posible de manera homogénea y espontánea.
Para considerar el gas desde sus partículas es necesario un modelo en el que se cumplan ciertos postulados o suposiciones; postulados que lógicamente deben poder predecir y explicar (lo más fiel posible) las observaciones macroscópicas y experimentales. Dicho esto, se mencionan y describen los postulados de la TCM.
En un recipiente colmado con partículas gaseosas, estas se dispersan y alejan entre ellas por todos los rincones. Si por un momento se pudieran reunir todas en un punto específico del recipiente, sin que haya licuefacción, se observaría que apenas ocupan una porción despreciable del volumen del recipiente.
Significa que en el recipiente, aunque contenga millones de partículas gaseosas, realmente se encuentra más vacío que lleno (relación volumen-vacío mucho menor que 1); por lo tanto, si sus barreras lo permiten, él y el gas en su interior puede comprimirse de manera brusca; ya que al fin de cuenta las partículas son muy pequeñas, al igual que su volumen.
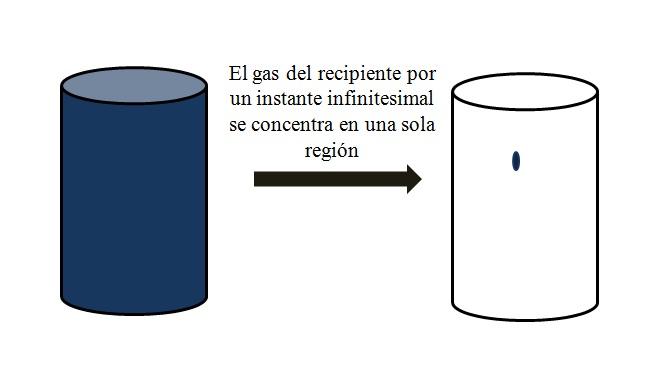
La imagen superior ilustra con precisión lo comentado arriba, empleando un gas de color azulado.
Las partículas gaseosas dentro del recipiente colisionan entre sí sin el tiempo suficiente para que sus interacciones cobren fuerza; aún menos cuando lo que principalmente les rodea es vacío molecular. Una inmediata consecuencia de esto es que sus trayectorias lineales les permiten abarcar completamente el volumen del recipiente.
Si lo anterior no fuera así, un recipiente con forma “estrambótica” y “laberíntica” tendría regiones húmedas producto de la condensación del gas; en lugar de esto, las partículas recorren todo el recipiente con plena libertad, sin la fuerza de sus interacciones deteniéndolas.

Las trayectorias lineales de la imagen superior (A.) demuestran este postulado; mientras que si las trayectorias son curvas (B.), evidencia que existen interacciones que no pueden ignorarse entre las partículas.
A partir de los primeros dos postulados converge por añadidura el hecho de que las partículas del gas jamás dejan de moverse. Una vez difuminadas en el recipiente, colisionan entre sí y con las paredes del mismo, con una fuerza y velocidad directamente proporcionales a la temperatura absoluta; esta fuerza es, la presión.
Si las partículas gaseosas dejaran de moverse por un instante, se presenciaría dentro del recipiente “lenguas de humo”, surgidas de la nada, con el tiempo suficiente para ordenarse en el vacío y dar formas aleatorias.
Si dentro del recipiente predominan únicamente las colisiones elásticas entre las partículas gaseosas y las paredes del recipiente, no se producirá nunca (mientras las condiciones físicas no cambien) la condensación del gas; o lo que es igual a decir que no descansan nunca y siempre están colisionando.
Esto se debe porque en las colisiones elásticas no existe pérdida neta de la energía cinética; una partícula colisiona con la pared y rebota a la misma velocidad. Si una partícula al colisionar disminuye la velocidad, la otra se acelera, sin que se produzca calor o sonido que disipen la energía cinética de ninguna de ellas.
El movimiento de las partículas es aleatorio y caótico, de modo que no todas llevan la misma velocidad; tal como sucede, por ejemplo, en una autopista o en una muchedumbre. Algunas son más energéticas y viajan con mayor velocidad, mientras que otras son lentas, esperando que una colisión las acelere.
Para describir su velocidad, es necesario entonces calcular un promedio; y con ello, se obtiene a su vez la energía cinética promedio de las partículas o moléculas gaseosas. Como la energía cinética de todas las partículas está en constante cambio, el promedio permite un mejor control de los datos y se puede trabajar con mayor confiabilidad.
La energía cinética molecular promedio (ECmp) en un recipiente se modifica con la temperatura. A mayor temperatura, mayor será dicha energía. Por tratarse de un promedio, puede haber partículas o gaseosas que tengan mayor o menor energía respecto a este valor; unas más rápidas y otras más lentas, respectivamente.
Matemáticamente puede demostrarse que ECmp depende exclusivamente de la temperatura. Esto significa que no importa cuál sea el gas, su masa o estructura moleculares, su ECmp será el mismo a una temperatura T y solo variará si esta aumenta o disminuye. De todos los postulados quizás este sea el más relevante.
¿Y qué hay de la velocidad molecular promedio? A diferencia de la ECmp, la masa molecular sí influye en la velocidad. Mientras más pesada sea la partícula o molécula gaseosa, es natural esperar que se desplace con mayor lentitud.
A continuación se mencionarán unos breves ejemplos de cómo la TCM ha logrado dar explicaciones a las leyes de los gases ideales. Aunque no se aborden, otros fenómenos, como la difusión y efusión de los gases, también pueden explicarse con la TCM.
Si el volumen del recipiente se comprime a temperatura constante, la distancia que deben recorrer las partículas gaseosas para colisionar contra las paredes disminuye; lo que es igual a un incremento de la frecuencia de dichas colisiones, resultando en una mayor presión. Al permanecer constante la temperatura, ECmp también es constante.
Si incrementa T, ECmp aumentará. Las partículas gaseosas se moverá con mayor rapidez y colisionarán un mayor número de veces con las paredes del recipiente; aumenta pues, la presión.
Si las paredes son flexibles, capaces de expandirse, su área se hará más grande y la presión caerá hasta volverse constante; y como resultado, el volumen también se incrementará.
Si en un espacioso recipiente se adicionaran varios litros de diferentes gases, provenientes de recipientes más pequeños, su presión total interna sería igual a la sumatoria de las presiones parciales ejercidas por cada tipo de gas por separado.
¿Por qué? Porque todos los gases comienzan a colisionar entre sí y a dispersarse homogéneamente; las interacciones entre ellos son nulas, y predomina el vacío en el recipiente (postulados de la TCM), por lo que es como si cada gas se encontrara solo, ejerciendo su presión de manera individual sin la intromisión de los otros gases.
- Whitten, Davis, Peck & Stanley. (2008). Química. (8va ed.). CENGAGE Learning, P 426-431.
- Fernández Pablo. (2019). Teoría Cinética Molecular. Vix. Recuperado de: vix.com
- Jones, Andrew Zimmerman. (07 de febrero de 2019). Kinetic Molecular Theory of Gases. Recuperado de: thoughtco.com
- Hall Nancy. (05 de mayo de 2015). Kinetic theory of gases. Glenn Research Center. Recuperado de: grc.nasa.gov
- Blaber M. & Lower S. (09 de octubre de 2018). Basics of Kinetic Molecular Theory. Chemistry LibreTexts. Recuperado de: chem.libretexts.org
- The Kinetic Molecular Theory. Recuperado de: chemed.chem.purdue.edu
- Wikipedia. (2019). Kinetic theory of gases. Recuperado de: en.wikipedia.org
- Toppr. (s.f.). Kinetic molecular theory of gases. Recuperado de: toppr.com
