Lente convergente: características, tipos y ejercicio resuelto
Las lentes convergentes son aquellas que son más gruesas en su parte central y más delgadas en los bordes. Como consecuencia de ello, concentran (hacen converger) en un único punto los rayos de luz que inciden sobre ellas de forma paralela al eje principal. Este punto recibe el nombre de foco, o foco imagen, y se representa con la letra F. Las lentes convergentes o positivas forman lo que se denomina imágenes reales de los objetos.
Un ejemplo típico de lente convergente es una lupa. Sin embargo, es habitual encontrar este tipo de lentes en dispositivos mucho más complejos como los microscopios o los telescopios. De hecho, un microscopio compuesto básico es el constituido por dos lentes convergentes que tienen una pequeña distancia focal. A estas lentes se las denomina objetivo y ocular.

Las lentes convergentes se utilizan en óptica para distintas aplicaciones si bien quizá la más conocida sea para corregir defectos de la vista. Así, son indicadas para tratar la hipermetropía, la presbicia y también algunos tipos de astigmatismo como el astigmatismo hipermetrópico.
Índice del artículo
- 1 Características
- 2 Elementos de las lentes convergentes
- 3 Formación de las imágenes en las lentes convergentes
- 4 Tipos de lentes convergentes
- 5 Diferencia con las lentes divergentes
- 6 Ecuaciones de Gauss de las lentes delgadas y aumento de una lente
- 7 Ejercicio resuelto
- 8 Referencias
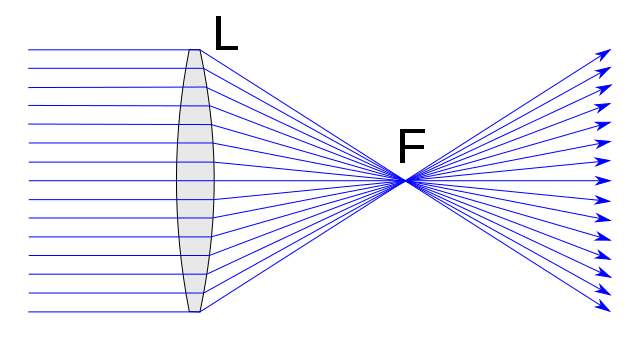
Las lentes convergentes cuentan con una serie características que las definen. En cualquier caso, quizá la más importante sea la que ya hemos adelantado en su definición. Así, las lentes convergentes se caracterizan por desviar a través del foco cualquier rayo que incide sobre ellas en una dirección paralela al eje principal.
Además, de forma recíproca, cualquier rayo incidente que pasa el foco se refracta paralelo al eje óptico de la lente.
De cara a su estudio, es importante conocer qué elementos constituyen las lentes en general y las lentes convergentes en particular.
En general, se denomina centro óptico de una lente al punto por el cual todo rayo que pasa por él no experimenta ninguna desviación.
El eje principal es la recta que une el centro óptico y el foco principal, que ya hemos comentado que se representa con la letra F.
Se denomina foco principal al punto en el que se encuentran todos los rayos que inciden en la lente paralelamente al eje principal.
Se denomina distancia focal la distancia que existe entre el centro óptico y el foco.
Los centros de curvatura se definen como los centros de las esferas que crean la lente; siendo, por su parte, los radios de curvatura los radios de las esferas que dan origen a la lente.
Y, por último, se denomina plano óptico al plano central de la lente.
De cara a la formación de las imágenes en las lentes convergentes se deben tener en cuenta una serie de reglas básicas que se explican a continuación.
Si el rayo incide sobre la lente de forma paralela al eje, el rayo emergente converge en el foco imagen. De forma inversa, si un rayo incidente atraviesa el foco objeto, el rayo emerge en una dirección paralela al eje. Por último, los rayos que atraviesan el centro óptico se refractan sin experimentar ningún tipo de desviación.
Como consecuencia de ello, en una lente convergente se pueden dar las siguientes situaciones:
– Que el objeto se ubique respecto del plano óptico a una distancia superior al doble de la distancia focal. En ese caso, la imagen que se produce es real, invertida y de menor tamaño que el objeto.
– Que el objeto se sitúe a una distancia del plano óptico igual al doble de la distancia focal. Cuando esto sucede, la imagen que se obtiene es una imagen real, invertida y del mismo tamaño que el objeto.
– Que el objeto esté a una distancia del plano óptico comprendida entre una vez y dos veces la distancia focal. Entonces, se produce una imagen es real, invertida y de mayor tamaño que el objeto original.
– Que el objeto se sitúe a una distancia del plano óptico inferior a la distancia focal. En ese caso, la imagen será virtual, directa y de mayor tamaño que el objeto.
Existen tres tipos distintos de lentes convergentes: lentes biconvexas, lentes planoconvexas y lentes cóncavoconvexas.
Las lentes biconvexas, como su nombre indica, se componen de dos superficies convexas. Las planoconvexas, por su parte, cuentan con una superficie plana y otra convexa. Y, por último, las lentes cóncavoconvexas están constituidas por una superficie ligeramente cóncava y otra convexa.

Las lentes divergentes, en cambio, se diferencian de las convergentes en que el espesor disminuye de los bordes hacia el centro. Así, al contrario de lo que ocurría con las convergentes, en este tipo de lentes los rayos de luz que inciden de forma paralela al eje principal se separan. De este modo, forman lo que se denomina imágenes virtuales de los objetos.
En óptica, las lentes divergentes o negativas, como también se las conoce, se emplean principalmente para corregir la miopía.
En general, el tipo de lentes que se estudian son las que se denomina como lentes delgadas. Estas se definen como aquellas que tienen un grosor pequeño en comparación con los radios de curvatura de las superficies que las limitan.
Este tipo de lentes se pueden estudiar con la ecuación de Gauss y con la ecuación que permite determinar el aumento de una lente.
La ecuación de Gauss de las lentes delgadas sirve para resolver multitud de problemas de óptica básica. De ahí su gran importancia. Su expresión es la siguiente:
1/f = 1/p +1/q
Donde 1/ f es lo que se denomina potencia de una lente y f es la distancia focal o distancia del centro óptico al foco F. La unidad de medida de la potencia de una lente es la dioptría (D), siendo 1 D = 1 m-1. Por su parte, p y q son respectivamente la distancia a la que ubica un objeto y la distancia a la que se observa su imagen.
El aumento lateral de una lente delgada se obtiene con la siguiente expresión:
M = – q / p
En donde M es el aumento. A partir del valor del aumento, se pueden deducir una serie de consecuencias:
Si |M| > 1, el tamaño de la imagen es mayor que el del objeto
Si |M| 1, el tamaño de la imagen es menor que el del objeto
Si M > 0, la imagen es derecha y en el mismo lado de la lente que el objeto (imagen virtual)
Si M 0, la imagen está invertida y en el lado contrario que el objeto (imagen real)
Un cuerpo se sitúa a un metro de distancia de una lente convergente, que tiene una distancia focal de 0, 5 metros. ¿Cómo será la imagen del cuerpo? ¿A qué distancia se encontrará?
Contamos con los siguientes datos: p = 1 m; f = 0,5 m.
Sustituimos estos valores en la ecuación de Gauss de las lentes delgadas:
1/f = 1/p +1/q
Y queda lo siguiente:
1/0,5 = 1 + 1/q; 2 = 1 + 1/q
Despejamos 1/q
1/q = 1
Para, a continuación, despejar q y obtener:
q = 1
De ahí, sustituimos en la ecuación del aumento de una lente:
M = – q / p = -1/1= -1
Por tanto, la imagen es real ya que q > 0, invertida porque M 0 y de igual tamaño dado que el valor absoluto de M es 1. Por último, la imagen se encuentra a un metro de distancia del foco.
- Luz (n.d.). En Wikipedia. Recuperado el 18 de marzo, 2019, desde es.wikipedia.org.
- Lekner, John (1987). Theory of Reflection, of Electromagnetic and Particle Waves. Springer.
- Light (n.d.). In Wikipedia. Recuperado el 20 de marzo, 2019, desde en.wikipedia.org.
- Lente (n.d.). En Wikipedia. Recuperado el 17 de marzo, 2019, desde es.wikipedia.org.
- Lens (optics). In Wikipedia. Recuperado el 19 de marzo, 2019, desde en.wikipedia.org.
- Hecht, Eugene (2002). Optics (4th ed.). Addison Wesley.
- Tipler, Paul Allen (1994). Física. 3ª Edición. Barcelona: Reverté.
