Proporcionalidad compuesta: explicación, regla de tres compuesta, ejercicios
La proporcionalidad compuesta o múltiple es la relación entre más de dos magnitudes, donde puede observarse proporcionalidad directa e inversa entre los datos y la incógnita. Se trata de una versión más avanzada de la proporcionalidad simple, aunque las técnicas empleadas en ambos procedimientos son similares.
Por ejemplo, si se necesitan 7 personas para descargar 10 toneladas de mercancía en 3 horas, la proporcionalidad compuesta puede usarse para calcular cuántas personas se necesitarán para descargar 15 toneladas en 4 horas.
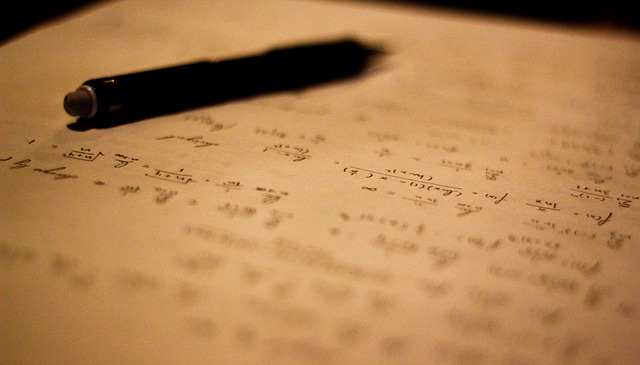
Para responder a esta pregunta, resulta conveniente hacer una tabla de valores para estudiar y relacionar las magnitudes e incógnitas.

Se procede a analizar los tipos de relaciones entre cada magnitud y la incógnita presente, que para este caso corresponde a la cantidad de personas que trabajarán.
A medida que aumenta el peso de la mercancía, también aumenta la cantidad de personas necesarias para descargarla. Debido a esto, la relación entre peso y trabajadores es directa.
Por otra parte, al aumentar la cantidad de trabajadores, las horas de trabajo disminuyen. Debido a ello, la relación entre personas y horas de trabajo es de tipo inverso.
Índice del artículo
- 1 Cómo calcular proporcionalidades compuestas
- 2 Explicación
- 3 Regla de tres directa
- 4 Regla de tres inversa
- 5 Condición
- 6 Verificación de resultados
- 7 Despeje
- 8 Historia
- 9 Ejercicios resueltos
- 10 Ejercicios propuestos
- 11 Referencias
Para resolver ejemplos como el anterior, se utiliza mayormente el método de la regla de tres compuesta. Este consiste en establecer los tipos de relaciones entre magnitudes e incógnitas para luego representar un producto entre fracciones.
Con respecto al ejemplo inicial, las fracciones correspondientes a la tabla de valores se organizan de la siguiente manera:
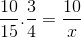
Pero antes de resolver y despejar la incógnita se deben invertir las fracciones correspondientes a la relación inversa. Que para este caso corresponden a la variable tiempo. De esta manera, la operación a resolver será:
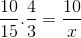
Cuya única diferencia es la inversión de la fracción correspondiente a la variable tiempo 4/3. Se procede a operar y despejar el valor de x.
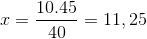
Así, se necesitan más de once personas para poder descargar 15 toneladas de mercancía en 4 horas o menos.
La proporcionalidad es la relación constante entre magnitudes que se encuentran sujetas a cambios, los cuales serán simétricos para cada una de las magnitudes involucradas. Existen relaciones directamente e inversamente proporcionales, definiendo así los parámetros de la proporcionalidad simple o compuesta.
Consiste en una relación de proporción entre variables, que presentan el mismo comportamiento al ser modificadas. Es muy frecuente en el cálculo de porcentajes referentes a magnitudes distintas de cien, donde se aprecia su estructura fundamental.
A manera de ejemplo se puede calcular el 15% de 63. A simple vista no puede apreciarse dicho porcentaje de manera sencilla. Pero implementando la regla de tres se puede realizar la siguiente relación: si el 100% es 63, entonces el 15%, ¿cuánto será?
100%———-63
15%———–X
Y la operación correspondiente es:
(15% . 63) / 100% = 9,45
Donde los signos de porcentaje se simplifican y se consigue la cifra 9,45 que representa el 15% de 63.
Como su nombre lo indica, en este caso la relación entre las variables es contraria. Se debe establecer la relación inversa antes de proceder al cálculo. Su procedimiento es homólogo al de la regla de tres directa, a excepción de la inversión en la fracción a calcular.
Por ejemplo, 3 pintores necesitan 5 horas para terminar una pared. ¿En cuántas horas la terminarían 4 pintores?
En este caso la relación es inversa, ya que al aumentar la cantidad de pintores el tiempo de trabajo debería disminuir. Se establece la relación;
3 pintores —— 5 horas
4 pintores—— X horas
Al ser inversa la relación, se invierte el orden de operación. Siendo esta la manera correcta;
(3 pintores) . (5 horas) / 4 pintores = 3,75 horas
Se simplifica el término pintores, y el resultado es 3,75 horas.
Para estar en presencia de una proporcionalidad compuesta o múltiple, es necesario encontrar ambos tipos de relación entre las magnitudes y variables.
– Directa: La variable presenta el mismo comportamiento que la incógnita. Es decir, que al aumentar o decrecer una, la otra se altera por igual.
– Inversa: La variable presenta un comportamiento antónimo al de la incógnita. Se debe invertir la fracción que define a dicha variable en la tabla de valores, con el fin de representar la relación inversamente proporcional entre variable e incógnita.
Es muy común confundir el orden de las magnitudes cuando se trabaja con proporcionalidades compuestas, a diferencia de lo que ocurre en los cálculos de proporción habituales, cuya naturaleza es mayormente directa y resoluble mediante regla de tres simple.
Por ello es importante examinar el orden lógico de los resultados, constatando la coherencia de las cifras arrojadas por la regla de tres compuesta.
En el ejemplo inicial, cometer dicho error implicaría obtener 20 como resultado. Esto es, 20 personas para descargar 15 toneladas de mercancía en 4 horas.
A simple vista no parece un resultado descabellado, pero resulta curioso un aumento de casi un 200% en el personal (de 7 a 20 personas) cuando el aumento de mercancía es de un 50%, e incluso con un mayor margen de tiempo para realizar la labor.
De esta forma la verificación lógica de los resultados representa un paso importante al implementar la regla de tres compuesta.
Aunque de naturaleza más básica con respecto a la formación matemática, el despeje representa un paso importante en los casos de proporcionalidad. Un despeje erróneo es suficiente para invalidar cualquier resultado obtenido en regla de tres simple o compuesta.
La regla de tres se hizo conocida en Occidente a través de los árabes, con publicaciones de varios autores. Entre ellos Al-Jwarizmi y Al-Biruni.
Al-Biruni, gracias a sus conocimientos multiculturales, tuvo acceso a vasta información referente a esta práctica en sus viajes a la India, siendo el responsable de la documentación más extensa sobre la regla de tres.
Plantea en su investigación, que la India fue el primer lugar donde se hizo común el uso de la regla de tres. El escritor asegura que era efectuada de manera fluida en sus versiones directa, inversa e incluso compuesta.
Aún se desconoce la fecha exacta en que la regla de tres pasó a formar parte de los conocimientos matemáticos de la India. Sin embargo, el documento más antiguo dirigido a esta práctica, el manuscrito de Bakhshali, fue descubierto en 1881. Actualmente se encuentra en Oxford.
Muchos historiadores de las matemáticas aseguran que este manuscrito data de principios de la presente era.
Una aerolínea debe trasladar 1535 personas. Se sabe que con 3 aviones le tomaría 12 días llevar hasta el último pasajero a destino. 450 personas más han llegado a la aerolínea y se ordena reparar 2 aviones para colaborar con esta tarea. ¿Cuántos días le tomará a la aerolínea trasladar hasta el último pasajero a su destino?
La relación entre la cantidad de personas y días de labor es directa, debido a que a mayor cantidad de personas, más días se requerirán para realizar esta labor.
Por otro lado la relación entre aviones y días es inversamente proporcional. Al aumentar la cantidad de aviones disminuyen los días necesarios para trasladar a la totalidad de pasajeros.
Se realiza la tabla de valores referentes a este caso.

Como se detalló en el ejemplo inicial, se debe invertir numerador y denominador en la fracción correspondiente a la variable inversa respecto de la incógnita. Quedando la operación de la siguiente manera:
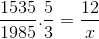
X = 71460/7675 = 9,31 días
Para trasladar a 1985 personas usando 5 aviones, son necesarios más de 9 días.
Una cosecha de maíz de 25 toneladas es llevada a los camiones de carga. Se sabe que el año anterior les tomó 8 horas con una nómina de 150 trabajadores. Si para este año la nómina aumento un 35%, ¿cuánto tiempo les tomará llenar los camiones de carga con una cosecha de 40 toneladas?
Antes de representar la tabla de valores se debe definir la cantidad de trabajadores para este año. Esta aumentó un 35% de la cifra inicial de 150 trabajadores. Para ello se usa una regla de tres directa.
100% ———- 150
35% ———– X
X = (35 . 100)/100 = 52,5. Este es el número de trabajadores adicionales con respecto al año anterior, obteniendo un número total de trabajadores de 203, desupés de redondear la cantidad obtenida.
Se procede a definir la tabla de datos correspondiente

Para este caso, el peso representa una variable de relación directa con la incógnita tiempo. Por otra parte la variable trabajadores maneja una relación inversa con el tiempo. A mayor número de trabajadores, la jornada será más breve.
Tomando en cuenta estas consideraciones e invirtiendo la fracción correspondiente a la variable trabajadores, se procede a calcular.

X = 40600 / 6000 = 6,76 horas
La jornada tardará poco menos de 7 horas.
– Defina el 73% de 2875.
– Calcule la cantidad de horas que duerme Teresa, si se conoce que solo duerme un 7% del total del día. Defina cuantas horas duerme a la semana.
– Un periódico publica 2000 copias cada 5 horas, usando solo 2 máquinas de impresión. ¿Cuantas copias producirá en 1 hora, si utiliza 7 máquinas? ¿En cuánto tiempo producirá 10.000 copias usando 4 máquinas?
- Enciclopedia Alvarez-iniciacion. A. Álvarez, Antonio Álvarez Pérez. EDAF, 2001.
- Manual completo de instruccion primaria elemental y superior: para uso de los aspirantes á maestros y especialmente de los alumnos de las Escuelas Normales de Provincia, Volumen 1. Joaquín Avendaño. Imprenta de D. Dionisio Hidalgo, 1844.
- Rational Approximation of Real Functions. P. P. Petrushev, Vasil Atanasov Popov. Cambridge University Press, 3 mar. 2011.
- Aritmética elemental para la enseñanza en las escuelas y colegios de la América Central. Darío González. Tip. Arenales, 1926.
- The Study of Mathematics: On the study and difficulties of mathematics. Augustus De Morgan. Baldwin and Cradock, 1830.
