Notación desarrollada: qué es, ejemplos y ejercicios
La notación desarrollada es aquella en la que una cifra numérica se expresa como una suma en la que se toma en cuenta el valor posicional de cada dígito que conforma el número.
Por ejemplo, cuando se escribe una cifra como 2345 cada dígito de la misma tiene una jerarquía posicional. Leyendo del dígito extremo derecho hacia la izquierda va creciendo la jerarquía o el valor.
En la cifra 2345, el dígito 5 representa cinco unidades, el dígito 4 representa cuatro decenas, el 3 corresponde a la tercera posición de izquierda a derecha y por tanto el 3 representa tres centenas, por último el 2 representa dos millares. Es decir en notación desarrollada o extendida la cifra 2345 se escribe así:
2345 = 2 millares + 3 centenas + 4 decenas + 5 unidades
Pero también puede expresarse de la siguiente manera:
2345 = 2 x 1000 + 3 x 100 + 4 x 10 + 5 x 1.
También la cifra 2345 puede escribirse como la suma de potencias de 10:
2345 = 2 x 10^3 + 3 x 10^2 + 4 x 10^1 + 5 x 10^0
Dónde el circunflejo ^ significa elevar al exponente indicado. Por ejemplo, 10^3 = 10 x 10 x 10 = 1000. Otra forma de escribir los exponentes es mediante un superíndice:
2345 = 2 x 103 + 3 x 102 + 4 x 101 + 5 x 100
Índice del artículo
- 1 Sistema de numeración posicional
- 2 Ejemplos de notación desarrollada
- 3 Ejercicios de notación desarrollada
- 4 Referencias
El sistema de números arábigos son los números que se usan cotidianamente en la gran mayoría de continentes y países del mundo. Los números arábigos son un sistema de base 10 porque se usan diez símbolos o grafemas para escribir cualquier número. Estos diez símbolos son:
0 1 2 3 4 5 6 7 8 9
Con uno solo de estos símbolos puede expresarse cifras comprendidas entre cero hasta nueve. Para expresar cifras mayores a nueve se emplea el sistema posicional en base diez. La cifra 10 es una decena y cero unidades. La cifra 11 es una decena y una unidad. La cifra 123 (ciento veintitrés) es una centena, dos decenas y tres unidades. Escrito en forma de potencias de diez el número 123 será:
1×10^2 + 2×10^1 + 3×10^0
Donde:
10^2 = 10 x 10 = 100
10^1 = 10
10^0 = 1.
Con este ejemplo queda claro que la posición del dígito en el extremo derecho es la posición 0 y representa el número de unidades, la del segundo dígito de derecha a izquierda es la posición 1 y representa el número de decenas, el tercer dígito (de derecha a izquierda) tiene posición 2 y representa los cientos.
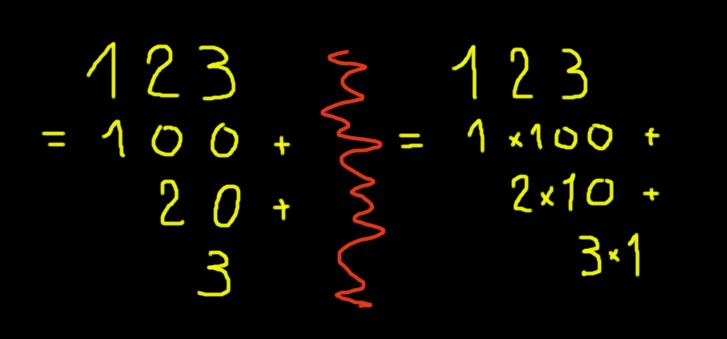
Con el sistema posicional decimal también es posible representar números o cifras que son menores que la unidad o que son mayores que la unidad pero no enteras, es decir que poseen fracciones de la unidad.
Para representar en el sistema decimal arábigo la fracción ½, es decir la mitad de la unidad se escribe:
½ =0,5
Para llegar a esta expresión en nuestro sistema en base 10 implícitamente se han hecho las siguientes operaciones:
1- Se multiplica numerador y denominador por 5 para tener la fracción equivalente 5/10 = 1/2.
2- Dividir entre 10 es equivalente a multiplicar por la potencia en base diez con exponente menos uno (10^-1), es decir 5/10 = 5×10^-1.
3- El exponente negativo indica cuántas veces se corre o posiciona hacia la derecha el dígito indicado a partir de la posición de la unidad, en nuestro caso sería 0,5.
4- ½ = 0,5 en notación extendida se escribe así:
0,5 = 0x10^0 + 5×10^-1
Donde 10^-1 = 0,1 es una décima (la fracción correspondiente a la unidad dividida en 10 partes iguales).
De esta forma, el número 0,5 corresponde a cinco décimas, pero el número 0,05 corresponde a 5 centésimas y el 0,005 a 5 milésimas.
Dada la cifra 40201 en notación estándar, convertirla a la notación desarrollada.
Solución:
4×10000 + 0x1000 + 2×100 + 0x10 + 1×1 = 40201
Escribir la fracción ¾ en notación extendida.
Solución:
En este caso se tienen tres cuartas partes de la unidad.
3/4 = 15/20 = 75/100 = 0,75 = 7/10 + 5/100 =
7×10^-1 + 5×10^-2.
Dicho en palabras quedaría así:
La fracción ¾ corresponde a siete décimas más cinco centésimas.
Decir en palabras la expresión desarrollada de la cifra 40201 del ejemplo 1.
Solución:
La notación desarrollada queda así:
40201 = 4×10000 + 0x1000 + 2×100 + 0x10 + 1×1
Que en lenguaje de palabras se dice:
Cuatro decenas de miles, más cero millares, más dos centenas, más cero decenas, más una unidad.
Expresar en palabras la cifra anterior y desglosar en forma desarrollada la frase correspondiente.
Solución:
La cifra 40201 en palabras se expresa así:
Cuarenta mil doscientos Uno
La frase anterior puede desarrollarse como:
40×1000 + 2×100 + 1
Puede decirse que la forma de pronunciar las cifras es una forma semidesarrollada de expresarla.
Escribir en forma desarrollada el número 7/3.
Solución:
Se trata de una cifra expresada como una fracción impropia, ya que como el numerador es mayor que el denominador, la cifra es mayor que la unidad.
Esta fracción impropia puede descomponerse como la suma de las fracciones 6/3 + 1/3. La primera de las fracciones da como resultado en número entero 2, mientras que 1/3 = 0,333333, donde el dígito 3 se repite indefinidamente. De modo que la expresión decimal desarrollada de la cifra 7/3 siempre será una expresión aproximada:
7/3 = 2 + 1/3 ≃ 2 + 0,333 = 2 + 3×10^-1 + 3×10^-2 + 3×10^-3.
Escribir en notación estándar y luego en forma desarrollada el número: Veintitrés millardos doscientos cincuenta millones quinientos veintiséis mil trescientos veinticinco con tres veintitrés milésimas.
Solución:
Cabe recordar que un millardo es el equivalente a mil millones. La palabra millardo fue aceptada por la Real Academia Española en 1995 a petición del fallecido presidente venezolano Rafael Caldera, miembro de la Academia Venezolana de la Lengua. En ese caso, la cifra del ejercicio en notación estándar se escribe así:
23.2501526.325,023
23 millardos + 250 millones + 526 miles + 325 unidades + 23 milésimas.
23×10^9 + 250×10^6 + 526×10^3 + 325×10^0 + 23×10^-3
Finalmente se escribe la cifra en notación desarrollada:
2×10^10 + 3×10^9 +2×10^8 + 5×10^7 + 0x10^6 + 5×10^5 + 2×10^4 + 6×10^3 + 3×10^2 + 2×10^1 + 5×10^0 + 0x10^-1 + 2×10^-2 + 3×10^-3.
- Khan Academy. Tablas de valor posicional. Recuperado de: es.khanacademy.org
- Khan Academy. Escribir un número en forma desarrollada (video). Recuperado de: es.khanacademy.org
- Ifrah, Geoges (1998): Historia universal de las cifras. Espasa Calpe S.A.
- Wikipedia. Notación posicional. Recuperado de: es.wikipedia.com
- Wikipedia. Millardo. Recuperado de: es.wikipedia.com
