Teoría de conjuntos: características, elementos, ejemplos, ejercicios
La teoría de conjuntos es una rama de la lógica-matemática que se encarga del estudio de las relaciones entre entidades denominadas conjuntos. Los conjuntos se caracterizan por ser colecciones de objetos de una misma naturaleza. Dichos objetos son los elementos del conjunto y pueden ser: números, letras, figuras geométricas, palabras que representan objetos, los objetos mismos y otros.
Fue Georg Cantor, hacia finales del siglo XIX, quien propuso la teoría de conjuntos. Mientras que otros notables matemáticos en el siglo XX hicieron su formalización: Gottlob Frege, Ernst Zermelo, Bertrand Russell, Adolf Fraenkel entre otros.

Los diagramas de Venn son la forma gráfica de representar a un conjunto, y consiste en una figura plana cerrada dentro de la cual están los elementos del conjunto.
Por ejemplo en la figura 1 se muestran dos conjuntos A y B, los cuales tiene elementos en común, los elementos comunes a A y a B. Estos forman un nuevo conjunto que se llama el conjunto intersección de A y B, que se escribe en forma simbólica de la siguiente manera:
A ∩ B
Índice del artículo
- 1 Características
- 2 Tipos de conjuntos
- 3 Elementos básicos
- 4 Ejemplos
- 5 Ejercicios resueltos
- 6 Referencias
El conjunto es un concepto primitivo como lo es en geometría el concepto de punto, recta o plano. No hay mejor manera de expresar el concepto que señalando ejemplos:
El conjunto E formado por los colores de la bandera de España. Esta forma de expresar el conjunto se llama por comprensión. El mismo conjunto E escrito por extensión es:
E = { rojo, amarillo }
En este caso, rojo y amarillo son elementos del conjunto E. Debe notarse que los elementos se enumeran entre llaves y no se repiten. En el caso de la bandera española hay tres franjas de colores (rojo, amarillo, rojo) dos de los cuales se repiten, pero los elementos no se repiten cuando se expresa el conjunto.
Suponga el conjunto V formado por las tres primeras letras vocales:
V = { a, e, i }
El conjunto potencia de V, que se denota por P(V) es el conjunto de todos los conjuntos que pueden formarse con los elementos de V:
P(V) ={ {a}, {e}, {i}, {a, e}, {a, i}, {e, i}, {a, e, i} }
Es un conjunto en el que sus elementos son numerables. Ejemplos de conjuntos finitos son las letras del abecedario español, las vocales del castellano, los planetas del sistema Solar entre otros. A el número de elementos de un conjunto finito se le llama su cardinalidad.
Se entiende por conjunto infinito todo aquel que el número de sus elementos es incontable, ya que sin importar lo grande que pueda ser el número de sus elementos siempre es posible encontrar más elementos.
Un ejemplo de conjunto infinito es el conjunto de los números naturales N, el cual en forma extensiva se expresa de la siguiente manera:
N = { 1, 2, 3, 4, 5, ….} es claramente un conjunto infinito, ya que no importa lo grande que pueda ser un número natural, siempre puede encontrarse el siguiente mayor, en un proceso sin fin. Claramente la cardinalidad de un conjunto infinito es ∞.
Es el conjunto que no contiene elemento alguno. El conjunto vacío V se denota por Ø o mediante una par de llaves sin elementos en su interior:
V = { } = Ø.
El conjunto vacío es único, por lo tanto debe es incorrecto decir “un conjunto vacío”, la forma correcta es decir “el conjunto vacío”.
Entre las propiedades del conjunto vacío se tiene que el mismo es subconjunto de cualquier conjunto:
Ø ⊂ A
Además, si un conjunto es subconjunto del conjunto vacío, entonces necesariamente dicho conjunto será el vacío:
A ⊂ Ø ⇔ A = Ø
Se llama conjunto unitario todo conjunto que contenga un solo elemento. Por ejemplo, el conjunto de los satélites naturales de la Tierra es un conjunto unitario, cuyo único elemento es la Luna. El conjunto B de los números enteros menores que 2 y mayores que cero solo tiene el elemento 1 por lo tanto es un conjunto unitario.
Un conjunto es binario si solo posee dos elementos. Por ejemplo el conjunto X, tal que x sea un número real solución de x^2 = 2. Este conjunto por extensión se escribe así:
X = { -√2, +√2 }
El conjunto universal es un conjunto que contiene otros conjuntos del mismo tipo o naturaleza. Por ejemplo, el conjunto universal de los números naturales es el conjunto de los números reales. Pero los números reales es conjunto universal también de los números enteros y de los números racionales.
En los conjuntos se pueden establecer varios tipos de relación entre ellos y sus elementos. Si dos conjuntos A y B tienen exactamente los mismos elementos entre ellos se establece una relación de igualdad que se denota así:
A = B
Si todos los elementos de un conjunto A pertenecen a un conjunto B, pero no todos los elementos de B pertenecen a A, entonces entre estos conjunto hay una relación de inclusión que se denota así:
A ⊂ B, pero B ⊄ A
La expresión anterior se lee: A es subconjunto de B, pero B no es subconjunto de A.
Para indicar que algún o algunos elementos pertenecen a un conjunto se usa el símbolo de pertenencia ∈, por ejemplo para decir que x elemento o elementos pertenecen al conjunto A se escribe simbólicamente así:
x ∈ A
Sí un elemento y no pertenece al conjunto A dicha relación se escribe así:
y ∉ A
La relación de pertenencia se da entre los elementos de un conjunto y el conjunto, con la única excepción del conjunto potencia, siendo el conjunto potencia la colección o conjunto de todos los conjuntos posibles que pueden formarse con los elementos de dicho conjunto.
Suponga V = { a,e,i } , su conjunto potencia es P(V) ={ {a}, {e}, {i}, {a, e}, {a, i}, {e, i}, {a,e,i} }, en ese caso el conjunto V pasa a ser un elemento del conjunto P(V) y puede escribirse:
V ∈ P(V)
La primera propiedad de la inclusión establece que todo conjunto está contenido en si mismo, o dicho de otra forma, que es subconjunto de sí mismo:
A ⊂ A
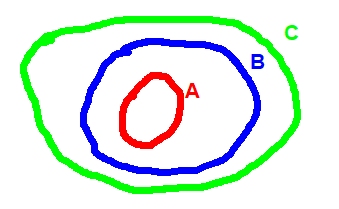
La otro propiedad de la inclusión es la transitividad: si A es subconjunto de B y B a su vez es subconjunto de C, entonces A es subconjunto de C. En forma simbólica la relación de transitividad se escribe así:
(A ⊂ B) ^ (B ⊂ C) => A ⊂ C
A continuación se muestra el diagrama de Venn correspondiente a la transitividad de la inclusión:
Intersección
La intersección es una operación entre dos conjuntos que da lugar a un nuevo conjunto perteneciente al mismo conjunto universal de los dos primeros. En ese sentido, es una operación cerrada.
Simbólicamente la operación de intersección se formula así:
A⋂B = { x / x∈A ^ x∈B }
Un ejemplo es el siguiente: el conjunto A de las letras de en la palabra “elementos” y el conjunto B de las letras de la palabra “repetidos”, la intersección entre A y B se escribe así:
A⋂B = { e, l, m, n, t, s } ⋂ { r, e, p, t, i, d, o, s } = { e, t, s } . El conjunto universal U de A, de B y también de A⋂B es el conjunto de las letras del alfabeto español.
Unión
La unión de dos conjuntos es el conjunto formado por los elementos comunes a los dos conjuntos y los elementos no comunes de los dos conjuntos. La operación de unión entre conjuntos se expresa simbólicamente así:
A∪B = { x/ x∈A v x∈B }
Diferencia
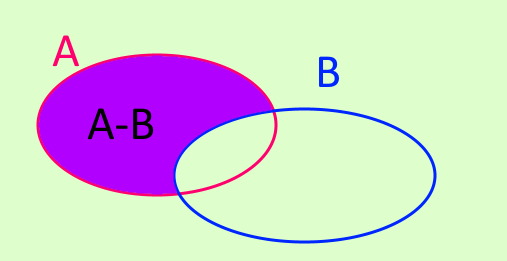
La operación de diferencia del conjunto A menos el conjunto B se denota por A-B. A-B es un nuevo conjunto formado por todos los elementos que están en A y que no pertenezcan a B. Simbólicamente se escribe así:
A – B = { x/ x ∈ A ^ x ∉ B }
Diferencia simétrica
La diferencia simétrica es una operación entre dos conjuntos donde el conjunto resultante está conformado por los elementos no comunes a los dos conjuntos. La diferencia simétrica simbólicamente se representa así:
A⊕B = { x/ x∈(A-B) ^ x∈(B-A) }
El diagrama de Venn es una forma gráfica de representar los conjuntos. Por ejemplo, el conjunto C de las letras de la palabra conjunto se representa así:

A continuación se muestra mediante diagramas de Venn que, el conjunto de las vocales en la palabra “conjunto”, es un subconjunto del conjunto de las letras de la palabra “conjunto”.

El conjunto Ñ de las letras del abecedario español es un conjunto finito, este conjunto por extensión se escribe así:
Ñ = { a, b, c, d, e, f, g, h, i, j, k, l, m, n, ñ, o, p, q, r, s, t, u, v, w, x, y, z } y su cardinalidad es 27.
El conjunto V de las vocales en español es un subconjunto del conjunto Ñ:
V ⊂ Ñ por lo tanto es un conjunto finito.
El conjunto finito V en forma extensiva se escribe así: V = { a, e, i, o, u } y su cardinalidad es 5.
Dados los conjuntos A = { 2, 4, 6, 8 } y B = { 1, 2, 4, 7, 9 } determine A-B y B-A.
A – B son los elementos de A que no están en B:
A – B = { 6, 8 }
B – A son los elementos de B que no están en A:
B – A = { 1, 7, 9 }
Escribir en forma simbólica y también por extensión el conjunto P de los números naturales pares menores que 10.
Solución: P = { x∈ N / x 10 ^ x mod 2 = 0 }
P = { 2, 4, 6, 8 }
Suponga el conjunto A aquel formado por los números naturales que son factores de 210, y el conjunto B aquel formado por los números naturales primos menores que 9. Determine por extensión ambos conjuntos y establezca qué relación hay entre los dos conjuntos.
Solución: Para determinar los elementos del conjunto A se debe comenzar por encontrar los factores del número natural 210:
210 = 2 * 3 * 5 * 7
Entonces el conjunto A se escribe:
A = { 2, 3, 5, 7 }
Pasamos a considerar el conjunto B, el cual es los primos menores que 9. El 1 no es primo porque no cumple la definición de primo: “un número es primo si y solo si tiene exactamente dos divisores el 1 y el propio número”. El 2 es par y a la vez es primo porque cumple la definición de primo, los otros primos menores que 9 son 3, 5 y 7. De modo que el conjunto B es:
B = { 2, 3, 5, 7 }
Por lo tanto los dos conjuntos son iguales: A = B.
Determine el conjunto cuyos elementos x son diferentes de x.
Solución: C = { x / x ≠ x }
Como todo elemento, número u objeto es igual a sí mismo, el conjunto C no puede ser otro más que el conjunto vacío:
C = Ø
Sea el conjunto de los N de los números naturales y Z el conjunto de los números enteros. Determine N ⋂ Z y N ∪ Z.
Solución:
N ⋂ Z = { x ∈ Z / x ≤ 0 } = (-∞, 0]
N ∪ Z = Z debido a que N ⊂ Z.
- Garo, M. (2014). Mathematics: quadratic equations: How solve a quadratic equation. Marilù Garo.
- Haeussler, E. F., & Paul, R. S. (2003). Matemáticas para administración y economía. Pearson Educación.
- Jiménez, J., Rodríguez, M., Estrada, R. (2005). Matemáticas 1 SEP. Umbral.
- Preciado, C. T. (2005). Curso de Matemáticas 3o. Editorial Progreso.
- Matemáticas 10 (2018). “Ejemplos de Conjuntos Finitos”. Recuperado de: matematicas10.net
- Wikipedia. Teoría de conjuntos. Recuperado de: es.wikipedia.com
