Coeficiente de correlación: fórmulas, cálculo, interpretación, ejemplo
El coeficiente de correlación en estadística es un indicador que mide la tendencia de dos variables cuantitativas X e Y a tener una relación de linealidad o proporcionalidad entre ellas.
Generalmente, los pares de variables X e Y son dos características de una misma población. Por ejemplo, X puede ser la altura de una persona e Y su peso.
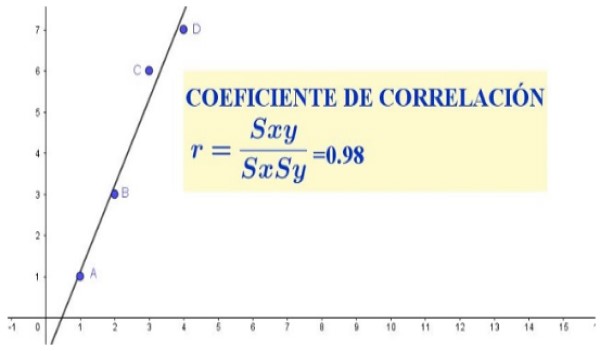
En este caso, el coeficiente de correlación indicaría si hay tendencia o no hacia una relación de proporcionalidad entre la altura y el peso de una población dada.
El coeficiente de correlación lineal de Pearson se denota con la letra r minúscula y sus valores mínimo y máximo son -1 y +1 respectivamente.
Un valor r = +1 indicaría que el conjunto de pares (X,Y) están perfectamente alineados y que cuando X crece, Y crecerá en la misma proporción. En cambio, si ocurriese que r = -1, el conjunto de pares también estaría perfectamente alineado, pero en tal caso cuando X crece, Y decrece en la misma proporción.
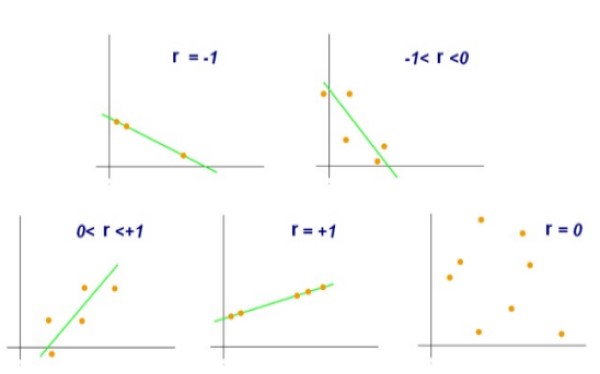
Por otro lado, un valor r = 0 indicaría que no hay correlación lineal alguna entre las variables X e Y. Mientras que un valor de r = +0,8 indicaría que los pares (X,Y) tienden a agruparse a un lado y otro de una cierta recta.
La fórmula para calcular el coeficiente de correlación r es la siguiente:
¿Cómo calcular el coeficiente de correlación?
El coeficiente de correlación lineal es una cantidad estadística que se encuentra incorporada en las calculadoras científicas, en la mayoría de las hojas de cálculo y en los programas estadísticos.
Sin embargo, conviene saber cómo se aplica la fórmula que lo define, y para ello se mostrará un cálculo detallado, llevado a cabo sobre un conjunto de datos pequeño.
Y tal como se dijo en la sección anterior, el coeficiente de correlación es la covarianza Sxy dividida entre el producto de la desviación estándar Sx para la variables X y Sy para la variable Y.
Covarianza y varianza
La covarianza Sxy es:
Sxy = [ Σ (Xi –
Donde la sumatoria va desde 1 hasta los N pares de datos (Xi, Yi).
Por su parte, la desviación estándar para la variable X es la raíz cuadrada de la varianza del conjunto de datos Xi, con i de 1 a N:
Sx = √ [Σ (Xi –
En forma similar, la desviación estándar para la variable Y es la raíz cuadrada de la varianza del conjunto de datos Yi, con i de 1 a N:
Sy = √ [Σ (Yi –
Caso ilustrativo
Con la finalidad de mostrar con detalle la forma de realizar el cálculo del coeficiente de correlación, tomaremos el siguiente conjunto de cuatro pares de datos
(X, Y): {(1, 1); (2, 3); (3, 6) y (4, 7)}.
En primer lugar calculamos la media aritmética para X e Y, como sigue:
Luego se calculan los restantes parámetros:
Covarianza Sxy
Sxy = [ (1 – 2.5)(1 – 4.25) + (2 – 2.5)(3 – 4.25) + (3 – 2.5)(6 – 4.25) +…. ….(4 – 2.5)(7 – 4.25) ] / (4-1)
Sxy = [ (-1.5)(-3.25) + (-0.5)(-1.25) + (0.5)(1.75) +….
….(1.5)(2.75) ] / (3) = 10.5 / 3 = 3.5
Desviación estándar Sx
Sx = √ [ (-1.5)2 + (-0.5)2 + (0.5)2 + (1.5)2) / (4-1)] = √[5/3] = 1.29
Desviación estándar Sy
Sx = √ [ (-3.25)2 + (-1.25)2 + (1.75)2 + (2.75)2) / (4-1)] =
√[22.75/3] = 2.75
Coeficiente de correlación r
r = 3.5 / (1.29 * 2.75) = 0.98
Interpretación
En el conjunto de datos del caso anterior se observa una fuerte correlación lineal entre las variables X e Y, que se manifiesta tanto en el gráfico de dispersión (que se aprecia en la figura 1) como en el coeficiente de correlación, el cual arrojó un valor bastante cercano a la unidad.
En la medida que el coeficiente de correlación sea más cercano a 1 o a -1, más sentido tiene el ajuste de los datos a una recta, resultado de la regresión lineal.
Regresión lineal
La recta de regresión lineal se obtiene del método de los mínimos cuadrados. en el que los parámetro de la recta de regresión se obtienen a partir de la minimización de la suma del cuadrado de la diferencia entre el valor Y estimado y el Yi de los N datos.
Por su parte, los parámetros a y b de la recta de regresión y = a + bx, obtenidos por el método de los mínimos cuadrados, son:
*b= Sxy / (Sx2) para la pendiente
*a=
Recordemos que Sxy es la covarianza definida más arriba y Sx2 es la varianza o el cuadrado de la desviación estándar antes definida.
Ejemplo
El coeficiente de correlación se usa para determinar si hay correlación de tipo lineal entre dos variables. Es aplicable cuando las variables a ser estudiadas son de tipo cuantitativo y además, se supone que ellas siguen una distribución de tipo normal.
Un ejemplo ilustrativo lo tenemos a continuación: una medida del grado de obesidad es el índice de masa corporal, el cual se obtiene al dividir el peso de una persona en kilogramos entre la altura al cuadrado de la misma en unidades de metros al cuadrado.
Se desea saber si hay una correlación fuerte entre el índice de masa corporal y la concentración de colesterol HDL en sangre, medida en milimoles por litro. Para este fin se ha hecho un estudio con 533 personas que se resume en el siguiente gráfico, en el que cada punto representa los datos de una persona.
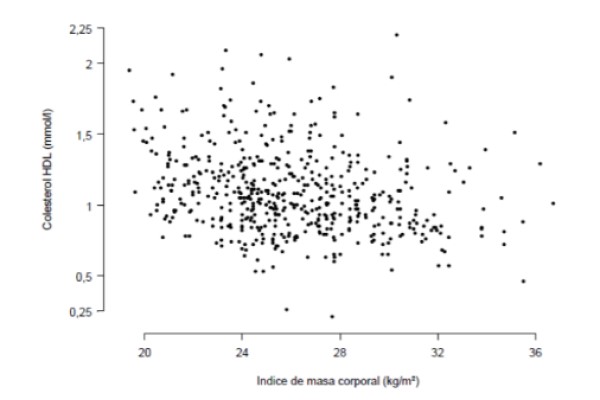
De la observación cuidadosa de la gráfica, se deduce que existe cierta tendencia lineal (no muy marcada) entre la concentración de colesterol HDL y el índice de masa corporal. La medida cuantitativa de esta tendencia es el coeficiente de correlación que para este caso resultó ser r = -0,276.
Referencias
- González C. Estadística General. Recuperado de: tarwi.lamolina.edu.pe
- IACS. Instituto Aragonés de Ciencias de Salud. Recuperado de: ics-aragon.com
- Salazar C. y Castillo S. Principios básicos de estadística. (2018). Recuperado de: dspace.uce.edu.ec
- Superprof. Coeficiente de correlación. Recuperado de: superprof.es
- USAC. Manual de estadística descriptiva. (2011). Recuperado de: estadistica.ingenieria.usac.edu.gt
- Wikipedia. Coeficiente de correlación de Pearson. Recuperado de: es.wikipedia.com.
