Energía libre de Helmholtz: unidades, cómo se calcula, ejercicios resueltos
La energía libre de Helmholtz es un potencial termodinámico que mide el trabajo útil de un sistema cerrado en condiciones de temperatura y volumen constantes. La energía libre de Helmholtz se denota como F y se define como la diferencia de la energía interna U menos el producto de la temperatura T por la entropía S:
F = U – T⋅S
Puesto que se trata de energía, se mide en Joules en el Sistema Internacional (SI), aunque otras unidades apropiadas pueden ser también ergios (CGS), calorías o electrón voltios (eV).

La variación negativa de la energía de Helmholtz durante un proceso se equipara con el trabajo máximo que el sistema puede efectuar en un proceso isocórico, es decir, a volumen constante. Cuando el volumen no se mantiene constante, parte de este trabajo puede efectuarse sobre el entorno.
En este caso nos referimos a trabajo en el que no varía el volumen, como por ejemplo el trabajo eléctrico: dW= Φdq, con Φ como el potencial eléctrico y q como la carga eléctrica.
Si además la temperatura es constante, la energía de Helmholtz se minimiza cuando se alcanza el equilibrio. Por todo esto, la energía de Helmholtz es particularmente útil en procesos a volumen constante. En tal caso se tiene:
– Para un proceso espontáneo: ΔF 0
– Cuando el sistema está en equilibrio: ΔF = 0
– En un proceso no-espontáneo: ΔF > 0.
Índice del artículo
Tal como se dijo al comienzo, la energía de Helmholtz se define como “la energía interna U del sistema, menos el producto de la temperatura absoluta T del sistema, por la entropía S del sistema”:
F = U – T⋅S
Se trata de una función de la temperatura T y del volumen V. Los pasos para visualizar esto son los siguientes:
– Partiendo de la primera ley de la termodinámica, la energía interna U se relaciona con la entropía S del sistema y su volumen V para procesos reversibles mediante la relación siguiente diferencial:
dU = dQ – dW = TdS – PdV
De esto se deduce que la energía interna U es una función de las variables S y V, por lo tanto:
U = U(S,V)
– Ahora se toma la definición de F y se deriva:
dF = dU – d(TS) = dU – TdS – SdT
– Sustituyendo allí la expresión diferencial obtenida para dU en el primer paso, queda:
dF = TdS – PdV – TdS – SdT = -SdT – PdV
– Finalmente se concluye que F es función de la temperatura T y el volumen V y puede expresarse como:
F = F(T,V)
La energía de Helmholtz se puede aplicar como un criterio general de espontaneidad en sistemas aislados, pero antes conviene precisar algunos conceptos:
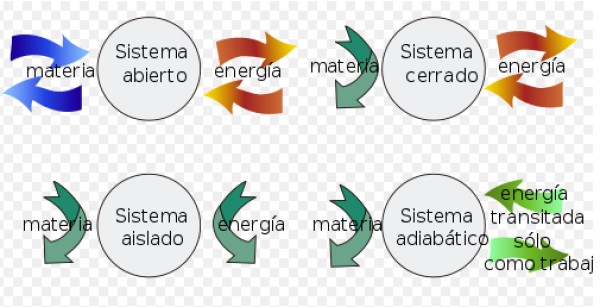
– Un sistema cerrado puede intercambiar energía con el entorno, pero no puede intercambiar materia.
– En cambio un sistema aislado no intercambia ni materia ni energía con el entorno.
– Por último un sistema abierto intercambia materia y energía con el entorno.
En los procesos reversibles la variación de la energía interna se calcula así:
dU = TdS – PdV
Ahora supongamos un proceso a volumen constante (isocórico), en el que el segundo término de la expresión anterior tiene contribución nula. Además debe recordarse que de acuerdo a la desigualdad de Clausius:
dS ≥ dQ/T
Tal desigualdad se aplica a un sistema termodinámico aislado.
De modo que para un proceso (reversible o no) en el que el volumen se mantenga constante se cumple:
T dS ≥ dU (a volumen fijo)
Tomando en cuenta que:
dF = dU – T dS
Tendremos que en un proceso isocórico a temperatura constante se cumple que: dF ≤ 0, tal como se indicó al comienzo.
De modo que la energía de Helmholtz F es una cantidad decreciente en un proceso espontáneo mientras se trate de un sistema aislado. F alcanza su valor mínimo y estable cuando se ha llegado al equilibrio reversible.
Calcular la variación de la energía libre de Helmholtz F para 2 moles de gas ideal a temperatura de 300K durante una expansión isotérmica que lleva al sistema de un volumen inicial de 20 litros hasta un volumen final de 40 litros.
Solución
Partiendo de la definición de F:
F = U – T S
Entonces una variación finita de F, llamada ΔF, será:
ΔF = ΔU – T ΔS
Como el enunciado afirma que la temperatura es constante: ΔT = 0. Ahora bien, en los gases ideales la energía interna sólo depende de su temperatura absoluta, pero como se trata de un proceso isotérmico, entonces ΔU = 0 y ΔF = – T ΔS. Para los gases ideales la variación de entropía de un proceso isotérmico se escribe así:
ΔS = n.R.ln(V2/V1)
Aplicando esta expresión:
ΔS = 2 moles x 8,314 J/(K mol) x ln(40L/ 20L) = 11,53 J/K
Finalmente, el cambio en la energía de Helmholtz es:
ΔF = – T ΔS = – 300K x 11,53 J/K = -3457,70 J.
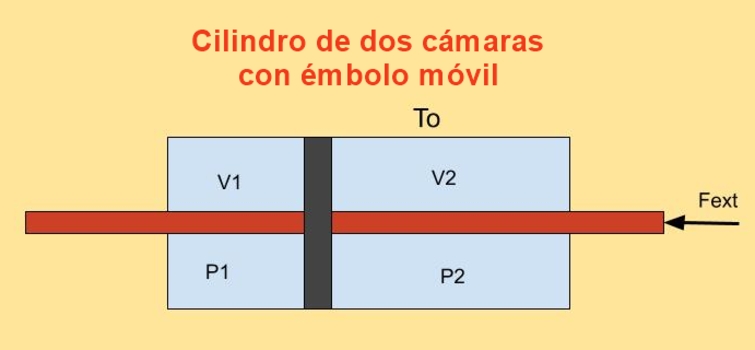
En el interior de un cilindro hay un pistón que lo divide en dos secciones y a cada lado del pistón hay n moles de un gas ideal monoatómico, como se muestra en la figura de abajo.
Las paredes del cilindro son buenas conductoras del calor (diatérmicas) y se encuentran en contacto con un reservorio de temperatura To.
El volumen inicial de cada uno de las secciones del cilindro son V1i y V2i, mientras que sus volúmenes finales son V1f y V2f después de un desplazamiento cuasiestático. El pistón se mueve por medio de un émbolo que atraviesa herméticamente las dos tapas del cilindro.
Se pide hallar:
a) El cambio en la energía interna del gas y el trabajo realizado por el sistema y
b) La variación de la energía de Helmholtz.
Solución a
Como el pistón se desplaza cuasiestáticamente, la fuerza externa aplicada sobre el émbolo debe equilibrar la fuerza debida a la diferencia de presión en las dos secciones del cilindro.
El trabajo dW realizado por la fuerza externa Fext durante un desplazamiento infinitesimal dx es:
dW = – Fext dx = (P1 – P2) a dx = P1 dV1 + P2 dV2
Donde se ha usado la relación dV1 = – dV2 = a dx, siendo a el área del émbolo. Por otra parte la variación de la energía de Helmholtz es:
dF = -SdT – PdV
Dado que durante el proceso la temperatura no cambia, entonces dT = 0 y dF = – PdV. Aplicando esta expresión a cada sección del cilindro se tiene:
dW = P1 dV1 + P2 dV2 = – dF1 – dF2
Siendo F1 y F2 las energías de Helmholtz en cada una de las cámaras.
El trabajo finito W puede calcularse a partir de la variación finita de la energía de Helmholtz de cada cámara:
W = -ΔF1 – ΔF2
Solución b
Para hallar el cambio de energía de Helmholtz se recurre a la definición: F = U – T S. Como en cada cámara se tiene un gas ideal monoatómico a temperatura constante To, la energía interna no cambia (ΔU=0), de modo que: ΔF = – To ΔS. Además:
ΔS = nR ln(Vf/Vi)
Que al sustituir permite finalmente que el trabajo realizado sea:
W = -To nR ln(V1f /V1i) -To nR ln(V2f /V2i) = -ΔF1 -ΔF2
W = – To nR ln[(V1f ⋅ V1i)/(V2f .V2i) ] = – ΔFtotal
Siendo ΔFtotal la variación total de la energía de Helmholtz.
- Castaños E. Ejercicios de energía libre. Recuperado de: lidiaconlaquimica.wordpress.com
- Libretexts. Helmholtz Energy. Recuperado de: chem.libretexts.org
- Libretexts. What are Free Energies. Recuperado de: chem.libretexts.org
- Wikipedia. Energía de Helmholtz. Recuperado de: es.wikipedia.com
- Wikipedia. Helmholtz free energy. Recuperado de: en.wikipedia.com
