Ondas estacionarias: fórmulas, características, tipos, ejemplos
Las ondas estacionarias son ondas que se propagan en un medio limitados, yendo y viniendo en una parte del espacio, a diferencia de las ondas viajeras, que al propagarse se alejan de la fuente que las originó y no regresan a ella.
Son la base de los sonidos producidos en los instrumentos musicales, ya que surgen fácilmente en las cuerdas fijas, ya sea en uno de sus extremos o en ambos. También se crean en membranas tensas como los tambores o en el interior de tubos y estructuras como puentes y edificios.
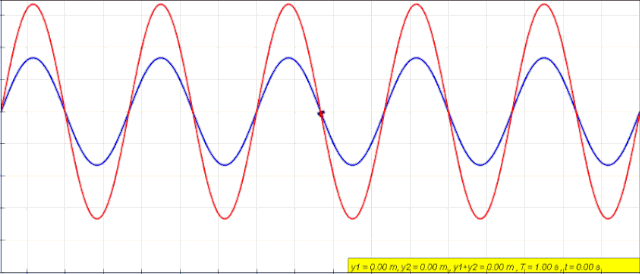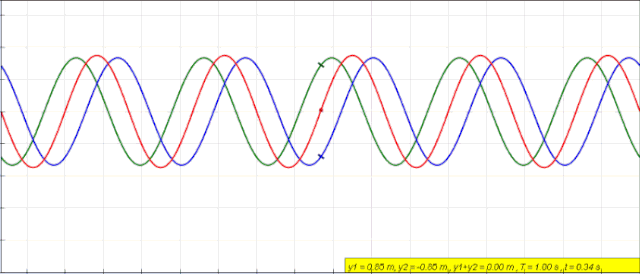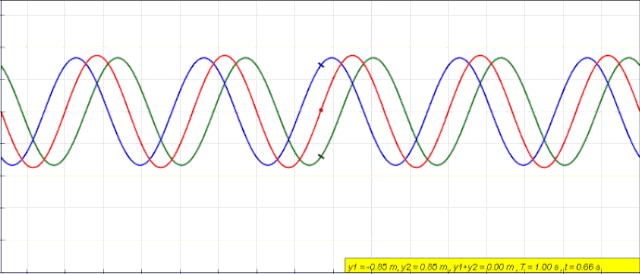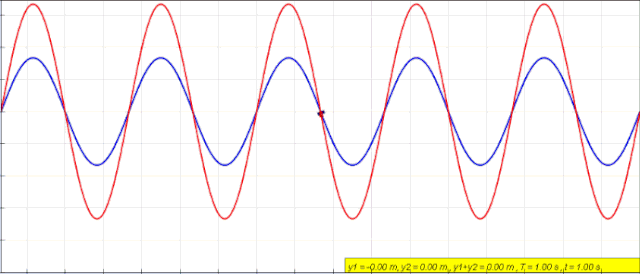
Cuando se tiene una cuerda fija en ambos extremos, como la de una guitarra, por ejemplo, se crean ondas con idénticas amplitud y frecuencia, que viajan en sentidos opuestos y se combinan produciendo un fenómeno llamado interferencia.
Si las ondas están en fase, las crestas y los valles están alineados y dan como resultado una onda con el doble de amplitud. En ese caso se habla de interferencia constructiva.
Pero si las ondas que interfieren están fuera de fase, las crestas de una se encuentran con los valles de otras y la amplitud que resulta es cero. Se trata entonces de interferencia destructiva.
Índice del artículo
- 1 Fórmulas y ecuaciones
- 2 Localización de nodos y vientres
- 3 Características de las ondas estacionarias
- 4 Tipos
- 5 Ejemplos de ondas estacionarias
- 6 Ejercicio resuelto
- 7 Referencias
Los principales elementos de la onda para representarla en espacio y tiempo son su amplitud A, su longitud de onda λ y su frecuencia angular ω.
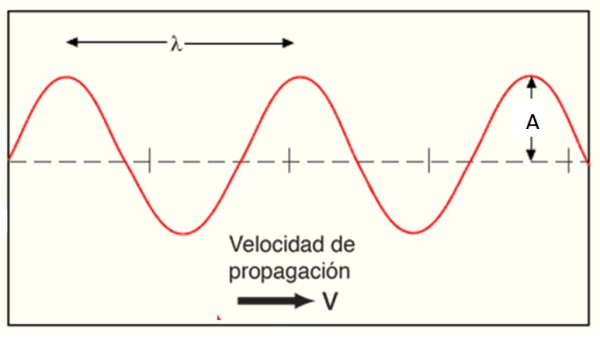
En la representación matemática se prefiere utilizar k, que el número de onda o número de veces que se sucede la onda por unidad de longitud. Por eso se define a través de la longitud de la onda λ que es la distancia entre dos valles o dos crestas:
k= 2π/ λ
Mientras que la frecuencia angular se relaciona con el período o duración de una oscilación completa, como:
ω = 2π/ T
Y además la frecuencia f viene dada por:
f = ω / 2π
Por lo tanto:
f = 1/T
Además las ondas se mueven con velocidad v según:
v = λ.f
Matemáticamente podemos expresar una onda mediante la función seno o la función coseno. Supongamos que se tienen ondas de igual amplitud A, longitud de onda λ y frecuencia ω, propagándose a lo largo de una cuerda y en sentidos opuestos:
y1 = A sen (kx – ωt)
y2 = A sen (kx + ωt)
Al sumarlas encontramos la onda resultante yR:
yR = y1 + y2 = A sen (kx – ωt) + A sen (kx + ωt)
Hay una identidad trigonométrica para encontrar la suma:
sen α + sen β = 2 sen (α+ β)/2 . cos (α – β)/2
Mediante esta identidad, la onda resultante yR queda:
yR = [2A sen kx] . cos ωt
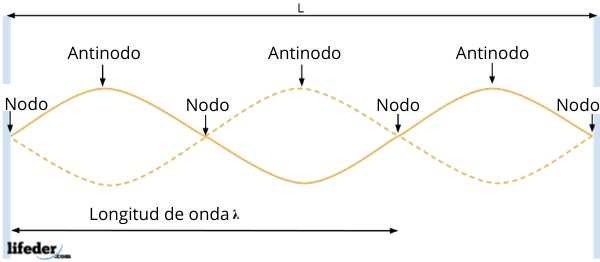
La onda resultante tiene amplitud AR = 2Asen kx, que depende de la posición de la partícula. Entonces, en los puntos para los cuales sen kx = 0, la amplitud de la onda se anula, es decir, no hay vibración.
Estos puntos son:
kx = π, 2π, 3π …
Como k = 2 π/ λ:
(2 π/ λ) x = π, 2π, 3π …
x = λ/2, λ, 3λ/2…
En tales puntos se produce interferencia destructiva y se llaman nodos. Están separados por una distancia igual a λ/2, como se deduce del resultado anterior.
Y entre dos nodos consecutivos están los antinodos o vientres, en los cuales la amplitud de la onda es máxima, ya que allí ocurre la interferencia constructiva. Se producen cuando:
sen kx = ± 1
kx = ± π/2, 3π/2, 5π /2…
De nuevo k = 2 π/ λ y entonces:
x = λ/4, 3λ /4, 5λ /4, …
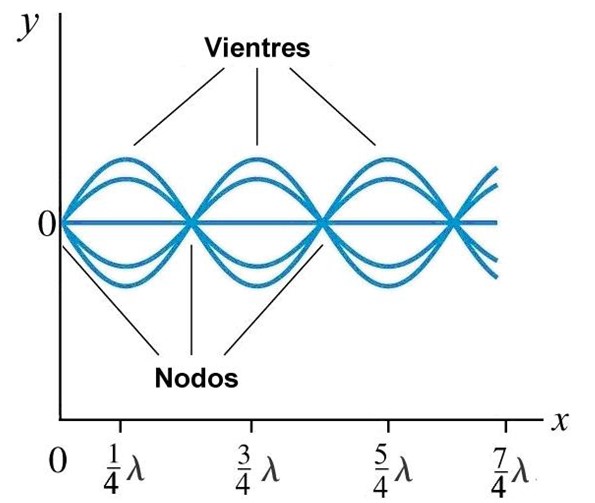
Las condiciones de frontera en la cuerda determinan cómo son las longitudes de onda y las frecuencias. Si una cuerda de longitud L está fija por sus dos extremos, no puede vibrar con cualquier frecuencia, porque los puntos donde la cuerda está fija ya son nodos.
Además la separación entre nodos adyacentes es λ/2, y entre nodo y vientre es λ/4, de esta manera solamente para ciertas longitudes de onda se producen ondas estacionarias: aquellas en las que se ajusta un número entero n de λ/2 dentro de L:
(λ/2) = L, con n= 1, 2, 3, 4….
Por lo tanto:
λ = 2L/n
Los armónicos
A los distintos valores que toma λ se le llaman armónicos. Así tenemos:
-Primer armónico: λ = 2L
-Segundo armónico: λ = L
-Tercer armónico: λ = 2 L/3
-Cuarto armónico: λ = L/2
Y así sucesivamente.
A pesar de que la onda estacionaria parece que no se mueve, aún sigue siendo válida la ecuación:
v = λ. f
Por lo tanto:
v = (2L/n) . f
f = nv/2L
Ahora bien, se puede demostrar que la velocidad con la que se desplaza una onda en una cuerda depende de la tensión T en la misma y de su densidad lineal de masa μ (masa por unidad de longitud) como:
Por lo tanto:
-Cuando las ondas son estacionarias, la onda resultante no se propaga igual que sus componentes, que van de un lado a otro. Hay puntos donde y = 0 porque no ha vibración: los nodos, en otras palabras, la amplitud AR se hace cero.
-La expresión matemática de una onda estacionaria consta del producto de una parte espacial (que depende de la coordenada x o de las coordenadas espaciales) y una parte temporal.
-Entre los nodos la onda resultante de color negro oscila en un solo lugar, mientras que las ondas que van de un lado a otro están desfasadas allí.
-Justo en los nodos no se transporta energía, ya que esta es proporcional al cuadrado de la amplitud, pero queda atrapada entre los nodos.
-La distancia entre nodos adyacentes es la mitad de la longitud de onda.
-Los puntos en los cuales la cuerda está fija también se consideran nodos.
Las ondas en una cuerda fija son ejemplos de ondas estacionarias en una dimensión, cuya descripción matemática ofrecimos en los apartados anteriores.
Las ondas estacionarias también pueden presentarse en dos y tres dimensiones, siendo su descripción matemática un poco más compleja.
-Una cuerda fija por extremo que se hace oscilar con la mano o con un pistón por el otro genera ondas estacionarias a lo largo de su longitud.

-Al tocar instrumentos de cuerda como la guitarra, el arpa, el violín y el piano también se crean ondas estacionarias, ya que tienen cuerdas ajustadas a distintas tensiones y fijas por ambos extremos.
También se crean ondas estacionarias en tubos con aire, como los tubos de los órganos.
Las ondas estacionarias surgen en estructuras como puentes y edificios. Un caso notable fue el del puente colgante Tacoma Narrows cerca de la ciudad de Seattle, Estados Unidos. Al poco tiempo de ser inaugurado en 1940, este puente se vino abajo a causa de las ondas estacionarias creadas en su interior por el viento.
La frecuencia del viento se emparejó con la frecuencia natural del puente, creando en ondas estacionarias en este, que fueron incrementando su amplitud hasta que el puente colapsó. El fenómeno se conoce como resonancia.
En los puertos se produce un fenómeno muy curioso llamado seiche, en el cual las olas del mar producen grandes oscilaciones. Esto se debe a que las aguas en el puerto están bastante encerradas, aunque las aguas oceánicas penetran cada cierto tiempo por la entrada del puerto.
Las aguas portuarias se mueven con su propia frecuencia, así como las del océano. Si ambas aguas igualan sus frecuencias se produce una gran ola estacionaria por resonancia, tal como sucedió con el puente de Tacoma.
Los seiches también pueden ocurrir en lagos, embalses, piscinas y otros cuerpos de agua limitados por superficies.
Se pueden crear ondas estacionarias en una pecera transportada por una persona, si la frecuencia con que camina la persona se iguala a la frecuencia del vaivén del agua.
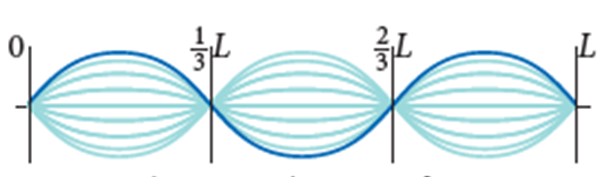
La cuerda de una guitarra tiene L = 0.9 m y densidad lineal de masa μ = 0.005 kg/m. Está sometida a 72 N de tensión y su modo de vibración es el que muestra la figura, con amplitud 2A = 0.5 cm.
Encontrar:
a) Velocidad de propagación
b) Frecuencia de la onda
c) La ecuación de la onda estacionaria correspondiente.
Mediante:
Se obtiene;
v = [72 N/( 0.005 kg/m)]1/2 = 120 m/s.
La distancia entre dos nodos adyacentes es λ/2, por lo tanto:
(2/3)L – (1/3) L = λ/2
(1/3) L = λ/2
λ = 2L/3 = 2 x 0.90 m / 3 = 0.60 m.
Como v = λ.f
f = (120 m/s)/ 0.60 m = 200 s-1= 200 Hz.
La ecuación es:
yR = [2A sen kx] . cos ωt
Necesitamos sustituir los valores:
k= 2π/ λ = k= 2π/ 0.60 m = 10 π/3
f = ω / 2π
ω = 2π x 200 Hz = 400 π Hz.
La amplitud 2A ya está dada por el enunciado:
2A = 0.5 cm = 5 x 10 -3 m.
Por lo tanto:
yR = 5 x 10 -3 m . sen[(10π/3)x] . cos(400πt) =
= 0.5 cm . sen[(10π/3)x] . cos(400πt)
- Bauer, W. 2011. Física para Ingeniería y Ciencias. Volumen 1. Mc Graw Hill.
- Figueroa, D. (2005). Serie: Física para Ciencias e Ingeniería. Volumen 7. Ondas y Física Cuántica. Editado por Douglas Figueroa (USB).
- Giancoli, D. 2006. Physics: Principles with Applications. 6th. Ed Prentice Hall.
- Serway, R., Jewett, J. (2008). Física para Ciencias e Ingeniería. Volumen 1. 7ma. Ed. Cengage Learning.
- Tipler, P. (2006) Física para la Ciencia y la Tecnología. 5ta Ed. Volumen 1. Editorial Reverté.
- Wikipedia. Seiche. Recuperado de: es.wikipedia.org.
