Trayectoria en física: características, tipos, ejemplos y ejercicios
La trayectoria en física es la curva que describe un móvil al pasar por sucesivos puntos durante su movimiento. Dado que este puede adoptar infinidad de variantes, así también serán las trayectorias que el móvil puede seguir.
Para ir de un sitio a otro, una persona puede tomar distintos caminos y distintas maneras: a pie a través de las aceras en calles y avenidas, o llegando en coche o moto por una autopista. Durante un paseo por el bosque, el caminante puede seguir una trayectoria complicada que incluya vueltas, subir o bajar de nivel y hasta pasar varias veces por un mismo punto.
Si los puntos por los que va transitando el móvil siguen una línea recta, la trayectoria será rectilínea. Esta es la trayectoria más simple, por ser unidimensional. Especificar la posición requiere de una sola coordenada.
Pero el móvil puede seguir una trayectoria curvilínea, pudiendo ser cerrada o abierta. En estos casos, el seguimiento de la posición requiere de dos o tres coordenadas. Se trata de movimientos en el plano y en el espacio respectivamente. Esto tiene que ver con los vínculos: condiciones materiales limitantes del movimiento. Algunos ejemplos son:
– Las órbitas que describen los planetas alrededor del sol son trayectorias cerradas con forma de elipse. Si bien, en algunos casos, se pueden aproximar a una circular, como en el caso de la Tierra.
– El balón que el guardameta patea en un saque de meta sigue una trayectoria parabólica.
– Un ave en vuelo describe trayectorias curvilíneas en el espacio, porque además de moverse sobre un plano, puede subir o bajar de nivel a voluntad.
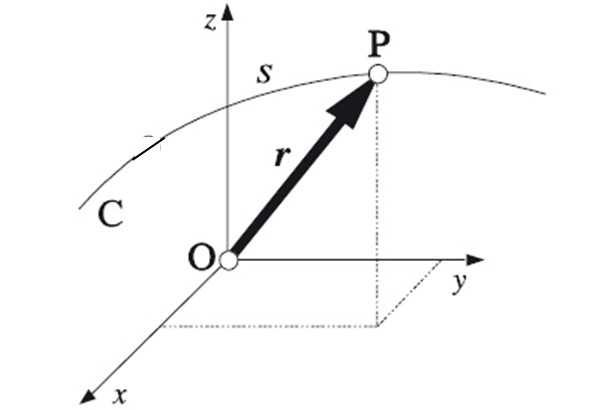
La trayectoria en física se puede expresar matemáticamente cuando se conoce la posición del móvil en cualquier instante de tiempo. Sea r el vector de posición, el cual a su vez tiene coordenadas x, y y z en el caso más general de un movimiento en tres dimensiones. Al conocer la función r (t) la trayectoria quedará completamente determinada.
Índice del artículo
En términos generales, la trayectoria puede ser una curva más bien complicada, sobre todo si se quiere expresar matemáticamente. Por eso, se comienza con los modelos más simples, donde los móviles viajan sobre una línea recta o bien sobre un plano, que puede ser el del piso o cualquier otro adecuado:
Las trayectorias más estudiadas son:
– Rectilínea, al transitar sobre una línea recta horizontal, vertical o inclinada. Una pelota arrojada verticalmente hacia arriba sigue esta trayectoria o un objeto que resbala cuesta abajo por un plano inclinado también. Son movimientos unidimensionales, bastando una sola coordenada para determinar su posición completamente.
– Parabólica, en la cual el móvil describe un arco de parábola. Es frecuente, ya que cualquier objeto lanzado oblicuamente bajo la acción de la gravedad (un proyectil) sigue esta trayectoria. Para especificar la posición del móvil hay que dar dos coordenadas: x y y.
– Circular, ocurre cuando la partícula en movimiento sigue una circunferencia. También es común en la naturaleza y en la práctica diaria. Muchos objetos cotidianos siguen una trayectoria circular como los neumáticos, piezas de maquinaria y satélites en órbita, por poner algunos ejemplos.
– Elíptica, el objeto se mueve siguiendo una elipse. Como se dijo al comienzo, es la trayectoria que siguen los planetas en órbita alrededor del sol.
– Hiperbólica, objetos astronómicos bajo la acción de una fuerza central (la gravedad), pueden seguir trayectorias elípticas (cerradas) o hiperbólicas (abiertas), siendo estas menos frecuentes que las primeras.
– Helicoidal, o movimiento en espiral, como el de un ave que asciende en una corriente térmica.
– Vaivén o pendular, el móvil describe un arco en movimientos de ida y vuelta.
Las trayectorias descritas en el apartado anterior son muy útiles para hacerse una idea rápidamente de cómo es el movimientos de un objeto. En todo caso, es necesario aclarar que la trayectoria de un móvil depende de la ubicación del observador. Esto significa que un mismo evento puede ser visto de formas diferentes, según donde se encuentre cada quien.
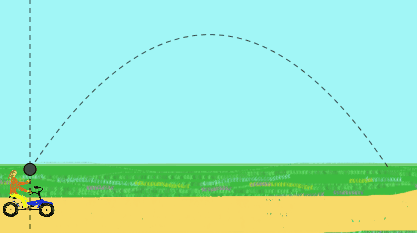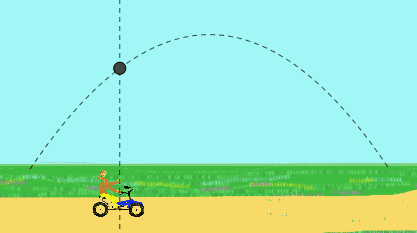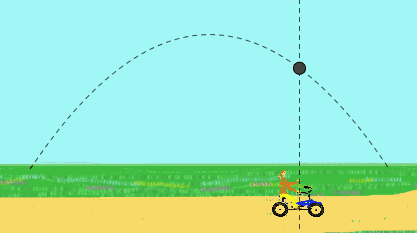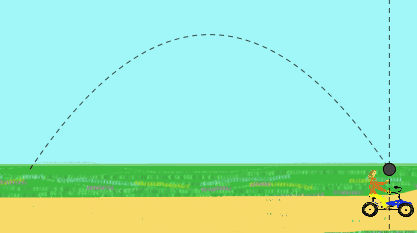
Por ejemplo una niña pedalea a velocidad constante y arroja hacia arriba una pelota. Ella observa que la pelota describe una trayectoria rectilínea.
Sin embargo para un observador parado en la vía que la ve pasar, la pelota tendrá un movimiento parabólico. Para él, la pelota fue lanzada inicialmente con una velocidad inclinada, resultado de la velocidad hacia arriba por la mano de la niña más la velocidad de la bicicleta.
– Explícita, especificando directamente la curva o lugar geométrico dado por la ecuación y (x)
– Implícita, en la cual una curva se expresa como f(x,y,z) = 0
–Paramétrica, en esta forma se dan las coordenadas x, y y z en función de un parámetro que, por lo general, se elige como el tiempo t. En este caso, la trayectoria se compone de las funciones: x(t),y(t) y z(t).
A continuación, se detallan dos trayectorias muy estudiadas en cinemática: la trayectoria parabólica y la trayectoria circular.
Lanzamiento inclinado en el vacío
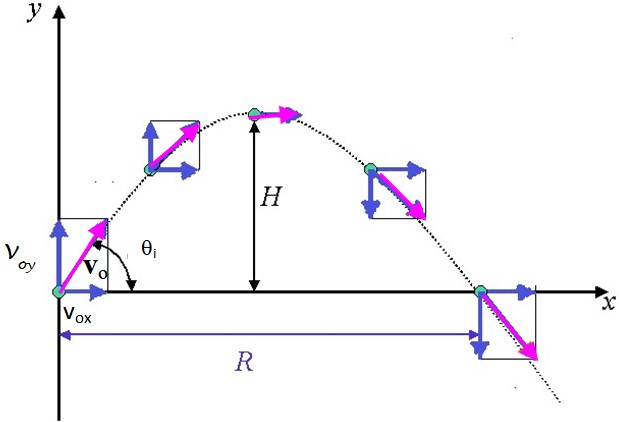
Se arroja un objeto (el proyectil) formando un ángulo a con la horizontal y con velocidad inicial vo como se muestra en la figura. No se toma en cuenta la resistencia del aire. El movimiento se puede tratar como dos movimientos independientes y simultáneos: uno horizontal con velocidad constante y otro vertical bajo la acción de la gravedad.
x (t) = xo +vox.t
y (t) =yo +voy.t -½g.t2
Estas ecuaciones son las ecuaciones paramétricas del lanzamiento de proyectiles. Tal como se explicó anteriormente, tienen común el parámetro t, que es el tiempo.
En el triángulo rectángulo de la figura se aprecia lo siguiente:
vox = vo cos θi
voy = vo sen θi
Al sustituir estas ecuaciones que contienen el ángulo de lanzamiento en las ecuaciones paramétricas resulta:
x(t) = xo +vo cos θi.t
y (t) =yo +vo. sen θi.t -½g.t2
Ecuación de la trayectoria parabólica
La ecuación explícita de la trayectoria se encuentra despejando t de la ecuación para x(t) y sustituyendo en la ecuación de y (t). Para facilitar el trabajo algebraico puede suponerse que el origen (0,0) se sitúa en el punto de lanzamiento y de esta forma xo = yo = 0.
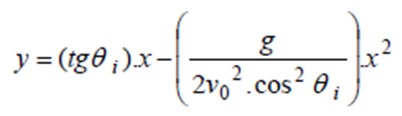
Esta es la ecuación de la trayectoria en forma explícita.
Trayectoria circular
Una trayectoria circular viene dada por:
(x – xo)2 + (y – yo)2 = R2
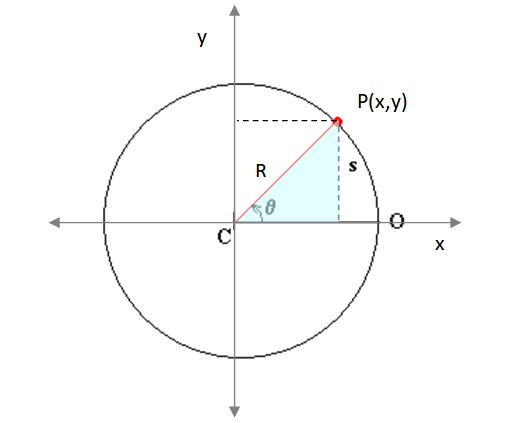
Aquí xo y yo representan el centro de la circunferencia descrita por el móvil y R es el radio de la misma. P(x,y) es un punto de la trayectoria. Del triángulo rectángulo sombreado (figura 3) se advierte que:
x = R. cos θ
y = R. sen θ
El parámetro, en este caso, es el ángulo barrido θ, llamado desplazamiento angular. En el caso particular de que la velocidad angular ω (ángulo barrido por unidad de tiempo) sea constante, se puede afirmar que:
θ= θo + ωt
Donde θo es la posición angular inicial de la partícula, que si se toma como 0, se reduce a:
θ = ωt
En tal caso, el tiempo regresa a las ecuaciones paramétricas como:
x = R.cos ωt
y = R. sen ωt
Los vectores unitarios i y j son muy convenientes para escribir la función de posición de un objeto r (t). Ellos indican las direcciones en el eje x y en el eje y respectivamente. En sus términos, la posición de una partícula que describe un Movimiento Circular Uniforme es:
r (t)= R.cos ωt i + R. sen ωt j
Un cañón puede disparar una bala con una velocidad de 200 m/s y un ángulo de 40º respecto a la horizontal. Si el lanzamiento se realiza en terreno plano y se desprecia la resistencia del aire, encuentre:
a) La ecuación de la trayectoria y (x)..
b) Las ecuaciones paramétricas x(t) y y(t).
c) El alcance horizontal y el tiempo que dura el proyectil en el aire.
d) La altura a la cual se encuentra el proyectil cuando x = 12.000 m
Solución a)
a) Para encontrar la trayectoria se sustituyen los valores dados en la ecuación y(x) de la sección precedente:
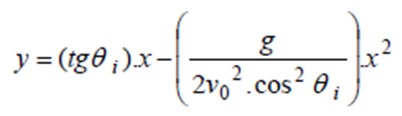
y (x) = tg 40º. x – {9.8/(2 ´ 4002. cos240º)} x2 ⇒ y (x) = 0.8391 x – 0.0000522x2
Solución b)
b) Se elige el punto de lanzamiento en el origen del sistema de coordenadas (0,0):
x (t) = xo +vox.t= 400´ cos 40º.t= 306.42. t.
y (t) =yo +voy.t -½g.t2=400 ´ sen 40º.t – 0.5 ´ 9.8´t2= 257.12 t – 4.9.t2
Solución c)
c) Para encontrar el tiempo que el proyectil dura en el aire, se hace y (t) =0, siendo el lanzamiento se hace en terreno plano:
0 = 257.12.t – 4.9.t2
t = 257.12 / 4.9 s = 52.473 s
El alcance máximo horizontal se encuentra sustituyendo este valor en x(t):
xmax = 306.42´ 52.47 m = 16077.7 m
Otra manera de encontrar xmax directamente es haciendo y = 0 en la ecuación de la trayectoria:
0 = 0.8391 xmax – 0.0000522 x2max
x = 0.8391 / 0.0000522 m = 16078.5 m
Hay una pequeña diferencia debido al redondeo de los decimales.
Solución d)
d) Para saber la altura cuando x = 12000 m se sustituye este valor directamente en la ecuación de la trayectoria:
y (12000) = 0.8391´ 12000 – 0.0000522´120002 m = 2552.4 m
La función de posición de un objeto viene dada por:
r (t) = 3t i + (4 -5t2) j m
Encontrar:
a) La ecuación para la trayectoria. ¿Qué curva es?
b) La posición inicial y la posición cuando t = 2 s.
c) El desplazamiento efectuado al cabo de t = 2 s.
Solución
a) La función de posición ha sido dada en términos de los vectores unitarios i y j, que determinan respectivamente la dirección en los ejes x y y, por lo tanto:
x(t) = 3t
y(t) = 4 -5t2
La ecuación de la trayectoria y (x) se encuentra despejando t de x (t) y sustituyendo en y(t):
t = x/3
y (x) = 4 –5. (x/3)2 = 4 – 5x2/9 (Parábola)
b) La posición inicial es: r (2) = 4 j m ; la posición en t = 2 s es r (2) = 6 i -16 j m
c) El desplazamiento Dr es la resta de los dos vectores de posición:
Δr = r (2) – r (2) = {6 i -16 j}– 4 j = 6 i – 20 j m
La Tierra tiene un radio R = 6300 Km y se sabe que el período de rotación de su movimiento alrededor de su eje es de un día. Encontrar:
a) La ecuación de la trayectoria de un punto sobre la superficie terrestre y su función de posición.
b) La velocidad y la aceleración de dicho punto.
Solución a)
a) La función de posición para un punto cualquiera en órbita circular es:
r (t)= R.cos ωt i + R.sen ωt j
Se tiene el radio de la Tierra R, pero no la velocidad angular ω, sin embargo se puede calcular del período, sabiendo que para el movimiento circular es válido decir que:
ω = 2π × frecuencia = 2π / período
El período del movimiento es: 1 día = 24 horas = 1440 minutos = 86400 segundos, por lo tanto:
ω = 2π / 86400 s = 0.000023148 s-1
Sustituyendo en la función de posición:
r (t)= R.cos ωt i + R. sen ωt j = 6300 (cos 0.000023148ti + sen 0.000023148tj) Km
La trayectoria en forma paramétrica es:
x(t) = 6300. cos 0.000023148t
y(t) = 6300. sen 0.000023148t
Solución b)
b) Para el movimiento circular, la magnitud de la velocidad lineal v de un punto está relacionada con la velocidad angular w mediante:
v = ωR = 0.000023148 s-1´ 6300 Km = 0.1458 Km/s = 145.8 m/s
Aún siendo un movimiento con rapidez constante de 145.8 m/s, existe una aceleración que apunta hacia el centro de la órbita circular, encargada de mantener al punto en rotación. Es la aceleración centrípeta ac, dada por:
ac = v2 / R = (145.8 m/s)2 / 6300 × 103 m = 0.00337 m/s2.
- Giancoli, D. Physics. (2006). Principles with Applications. 6th Prentice Hall. 22- 25.
- Kirkpatrick, L. 2007. Física: Una mirada al mundo. 6ta Edición abreviada. Cengage Learning. 23 – 27.
- Resnick, R. (1999). Física. Volumen 1. Tercera edición en español. México. Compañía Editorial Continental S.A. de C.V. 21-22.
- Rex, A. (2011). Fundamentos de Física. Pearson. 33 – 36
- Sears, Zemansky. (2016). University Physics with Modern Physics. 14th. Ed. Volume1. 50 – 53.
- Serway, R., Jewett, J. (2008). Física para Ciencias e Ingeniería. Volumen 1. 7ma. Edición. México. Cengage Learning Editores. 23-25.
- Serway, R., Vulle, C. (2011). Fundamentos de Física. 9na Ed. Cengage Learning. 43 – 55.
- Wilson, J. (2011). Fisica 10. Pearson Educación. 133 – 149.
