Esfuerzo cortante: cómo se calcula y ejercicios resueltos
Se conoce como esfuerzo cortante al que resulta de aplicar dos fuerzas paralelamente a una superficie y en sentido contrario. De esta forma se puede dividir a un objeto en dos partes, haciendo que las secciones deslicen una sobre otra.
Cotidianamente se aplican esfuerzos cortantes directos sobre telas, papeles o metales, ejercidos mediante tijeras, guillotinas o cizallas. También aparecen en estructuras tales como pernos o tornillos, pasadores, vigas, cuñas y soldaduras.

Es preciso aclarar que no siempre se pretende seccionar o cortar, pero el esfuerzo cortante sí tiende a deformar al objeto sobre el cual se aplica; por eso las vigas sometidas a esfuerzos cortantes tienden a combarse por su propio peso. Los siguientes ejemplos aclaran el punto.
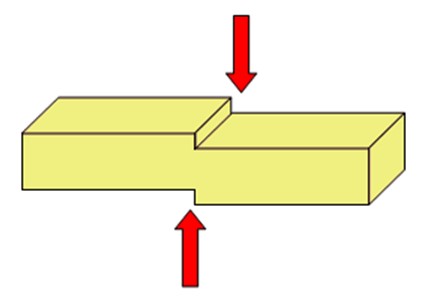
En la figura 2 se muestra un esquema sencillo para ilustrar lo antes dicho. Se trata de un objeto sobre el cual actúan dos fuerzas en direcciones contrarias. Hay un plano de corte imaginario (no está dibujado) y las fuerzas actúan una a cada lado del plano, cortando en dos la barra.
En el caso de una tijera: cada hoja o filo aplica una fuerza sobre la sección transversal (circular) del objeto a cortar, separándolo igualmente en dos partes, como el cordel de la figura 1.
Índice del artículo
- 1 El esfuerzo cortante puede ocasionar deformación
- 2 ¿Cómo se calcula el esfuerzo cortante?
- 3 Esfuerzo cortante y deformación
- 4 Ejercicios resueltos
- 5 Referencias
Se puede probar a ejercer un esfuerzo cortante deslizando la mano sobre la tapa de un libro cerrado. La otra tapa debe permanecer fija sobre la mesa, lo que se puede lograr apoyando la mano libre para que no se mueva. El libro se deformará un poco con esta acción, tal como se esquematiza en la siguiente figura:

Si se analiza esta situación cuidadosamente, se advierten las dos fuerzas ya referidas, pero esta vez aplicadas horizontalmente (en fucsia). Una es la de su mano sobre una cara y la otra es aplicada por la superficie de la mesa sobre la cara opuesta del libro que está fija.
El libro no gira, pese a que estas fuerzas podrían causar un torque o momento neto. Para evitarlo están las otras dos fuerzas verticales (en turquesa); la que se aplicó con la otra mano y la normal ejercida por la mesa, cuyo momento neto actúa en sentido contrario impidiendo el movimiento rotatorio.
Los esfuerzos cortantes aparecen incluso en el interior del cuerpo humano, ya que la sangre al circular ejerce continuamente fuerzas tangenciales sobre la cara interna de los vasos sanguíneos, causando pequeñas deformaciones en las paredes.
Su consideración es importante para determinar las posibilidades que tiene una estructura de fallar. En los esfuerzos cortantes se toma en cuenta no solamente la fuerza, sino también el área sobre la que actúa.
Esto se comprende de inmediato al tomar dos barras cilíndricas de la misma longitud, hechas con el mismo material pero de grosor diferente y sometiéndolas a esfuerzos cada vez mayores hasta que se rompan.
Evidentemente las fuerzas necesarias van a ser bien diferentes, porque una barra es más delgada que la otra; sin embargo el esfuerzo será el mismo.
El esfuerzo cortante se denota con la letra griega τ (tau) y se calcula como el cociente entre la magnitud de la fuerza aplicada F y el área A de la superficie sobre la cual actúa:
τpromedio= F /A
El esfuerzo así calculado es el que produce una fuerza promedio sobre la superficie en cuestión, ya que la fuerza no actúa sobre un punto único de la superficie, sino distribuida sobre toda ella y no de manera uniforme. Sin embargo la distribución puede representarse mediante una fuerza resultante actuando sobre un punto en particular.
Las dimensiones del esfuerzo cortante son de fuerza sobre superficie. En unidades del sistema internacional corresponden a newton/metro cuadrado, unidad denominada Pascal y abreviada Pa.
Son las mismas unidades de la presión, por lo tanto las unidades del sistema inglés como libra –fuerza/pie 2 y libra-fuerza /pulgada2 también son apropiadas.
En muchas situaciones la magnitud del esfuerzo cortante es proporcional a la deformación unitaria ocasionada en el objeto, como el libro del ejemplo anterior, el cual volverá a sus dimensiones originales en cuanto la mano se retire. En tal caso:
Esfuerzo cortante ∝ Deformación unitaria
La constante de proporcionalidad en este caso es el módulo de corte, módulo de rigidez o módulo de cizalla (G):
Esfuerzo cortante = Módulo de cizalla x Deformación unitaria
τ = G. γ
Con γ = ΔL/Lo, donde ΔL es la diferencia entre la longitud final y la inicial. Combinando las ecuaciones dadas, se puede encontrar una expresión para la deformación causada por el esfuerzo:

El valor de la constante G se encuentra en tablas y sus unidades son las mismas que las del esfuerzo, en vista de que la deformación unitaria es adimensional. Casi siempre el valor de G es la mitad o un tercio del valor de E, el módulo de elasticidad.
De hecho están relacionados mediante la expresión:

Donde ν es el módulo de Poisson, otra constante elástica del material cuyo valor está comprendido entre 0 y ½. Precisamente por eso G a su vez está comprendido entre E/3 y E/2.
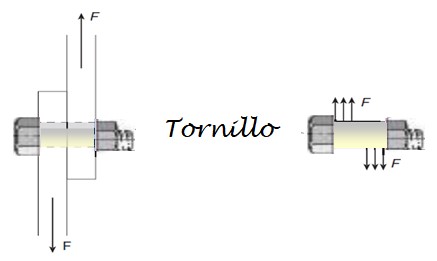
Para unir dos placas de hierro se usa un tornillo de acero, el cual debe resistir fuerzas cortantes de hasta 3200 N. ¿Cuál es el diámetro mínimo del tornillo si el factor de seguridad es 6.0? Se sabe que el material resiste hasta 170 x 106 N/m2.
Solución
El esfuerzo cortante al que está sometido el tornillo proviene de las fuerzas mostradas en la figura de abajo. El factor de seguridad es una cantidad adimensional y está relacionado con el esfuerzo máximo permisible:
Esfuerzo cortante = F/A = Esfuerzo máximo permisible/factor de seguridad
Por lo tanto el área es:
A = F x factor seguridad / Esfuerzo cortante = 3200 x 6 / 170 x 106 = 0.000113 m2
El área del tornillo viene dada por πD2/4, por lo tanto el diámetro es:
D2=4 x A/π = 0.000144 m2
D= 0.012 m = 12 mm.
Se emplea un pasador o taco de madera para impedir el giro de la polea sometida a las tensiones T1 y T2, con respecto a un eje de 3 pulgadas. Las dimensiones del pasador se muestran en la figura. Encontrar la magnitud del esfuerzo cortante sobre el taco, si sobre la polea actúan las fuerzas que se muestran:
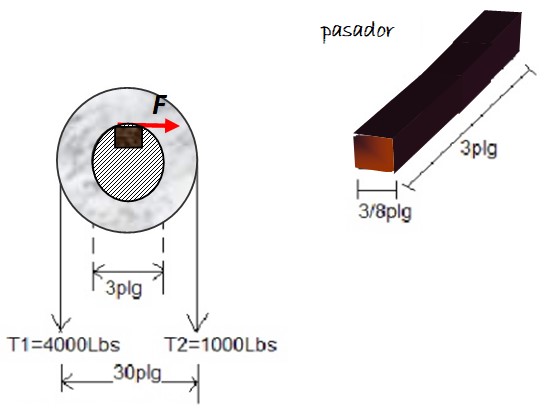
Solución
T1 produce un torque en sentido antihorario sobre la polea, al cual se asigna signo positivo, mientras que T2 produce torque en sentido horario con signo negativo. El brazo de palanca mide 15 pulgadas para cada tensión. Por lo tanto:
Torque neto = 4000 libras-fuerza . 15 pulgadas – 1000 libras-fuerza. 15 pulgadas = 45000 libras-fuerza . pulgada
El taco de madera no debe girar, luego los momentos respecto al centro del taco deben ser nulos. F representa la fuerza promedio sobre la superficie:
45.000 – F.d = 0
Con d =1.5 pulgadas, por lo tanto:
F x 1.5 = 45.000
F = 30.000 libras-fuerza
Esta fuerza ocasiona un esfuerzo cortante de magnitud:
τ = F/A = 30.000 libras-fuerza / (3/8 x 3) pulgada2 = 2.67 x 104 libras-fuerza/pulgada2
- Beer, F. 2010. Mecánica de materiales. 5ta. Edición. McGraw Hill. 7 – 9.
- Fitzgerald, 1996. Mecánica de Materiales. AlfaOmega. 21-23.
- Giancoli, D. 2006. Physics: Principles with Applications. 6th Ed. Prentice Hall. 238-242.
- Hibbeler, R.C. 2006. Mecánica de materiales. 6ta. Edición. Pearson Educación. 22 -25
- Valera Negrete, J. 2005. Apuntes de Física General. UNAM. 87-98.
- Wikipedia. Shear Stress. Recobrado de: en.wikipedia.org.
