Programación dinámica: características, ejemplo, ventajas, desventajas
La programación dinámica es un modelo de algoritmo que resuelve un problema complejo dividiéndolo en subproblemas, almacenando los resultados de los mismos para así evitar tener que volver a calcular esos resultados.
Esta programación se utiliza cuando se tienen problemas que se pueden dividir en subproblemas similares, de modo que sus resultados puedan ser reutilizados. En su gran mayoría, esta programación se utiliza para la optimización.
Antes de resolver el subproblema disponible, el algoritmo dinámico intentará examinar los resultados de los subproblemas previamente resueltos. Las soluciones de los subproblemas se combinan para así lograr la mejor solución.
En lugar de calcular el mismo subproblema una y otra vez, se podrá almacenar su solución en alguna memoria, al encontrarse por primera vez con este subproblema. Cuando el mismo aparezca nuevamente durante la solución de otro subproblema, se tomará la solución ya almacenada en la memoria.
Esta es una idea maravillosa para subsanar el tiempo con memoria, donde al utilizar espacio adicional se puede mejorar el tiempo requerido para encontrar una solución.
Índice del artículo
- 1 Características de la programación dinámica
- 2 Ejemplo
- 3 Ventajas
- 4 Desventajas
- 5 Aplicaciones
- 6 Referencias
Las siguientes características esenciales son las que debe tener un problema para que se pueda aplicar la programación dinámica:
Esta característica expresa que un problema de optimización se puede resolver al combinar las soluciones óptimas de los problemas secundarios que lo conforman. Estas subestructuras óptimas se describen mediante la recursividad.
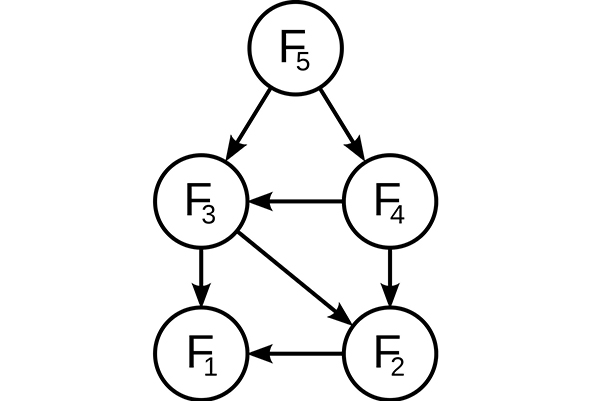
Por ejemplo, en un grafo se presentará una subestructura óptima en la ruta más corta r que va desde un vértice s hasta un vértice t:
Esto es, en esta ruta más corta r se puede tomar cualquier vértice intermedio i. Si r es realmente la ruta más corta, entonces se podrá dividir en las subrutas r1 (desde s hasta i) y r2 (desde i hasta t), de tal modo que estas sean a su vez las rutas más cortas entre los vértices correspondientes.
Por tanto, para encontrar las rutas más cortas se podrá formular fácilmente la solución de manera recursiva, que es lo que hace el algoritmo Floyd-Warshall.
El espacio de los subproblemas debe ser pequeño. Es decir, cualquier algoritmo recursivo que resuelva un problema deberá resolver los mismos subproblemas una y otra vez, en lugar de generar nuevos subproblemas.
Por ejemplo, para generar la serie de Fibonacci se puede considerar esta formulación recursiva: Fn= F(n–1) + F(n–2), tomando como caso base que F1= F2= 1. Entonces se tendrá que: F33= F32 + F31, y F32= F31 + F30.
Como se puede observar, F31 se está resolviendo en los subárboles recursivos tanto de F33 como de F32. Aunque el número total de subproblemas es realmente pequeño, si se adopta una solución recursiva como esta se terminarán resolviendo los mismos problemas una y otra vez.
Esto lo toma en cuenta la programación dinámica, por lo que resuelve cada subproblema solo una vez. Esto se puede lograr de dos maneras:
Enfoque de arriba hacia abajo
Si la solución a cualquier problema se puede formular recursivamente usando para ello la solución de sus subproblemas, y si estos subproblemas se superponen, entonces las soluciones a los subproblemas se podrán memorizar o almacenar fácilmente en una tabla.
Cada vez que se busque la solución de un subproblema nuevo, se revisará en la tabla si fue resuelto previamente. En caso que se tenga almacenada una solución, se utilizará la misma en lugar de calcularla de nuevo. De lo contrario, se resolverá el subproblema, almacenando la solución en la tabla.
Enfoque ascendente
Luego que se formula de forma recursiva la solución de un problema en términos de sus subproblemas, se podrá intentar reformular el problema de manera ascendente: primero se intentarán resolver los subproblemas y usar sus soluciones para llegar a soluciones a los subproblemas más grandes.
Esto también se hace generalmente en forma de tabla, generando iterativamente soluciones a subproblemas cada vez más grandes mediante el uso de soluciones a los subproblemas pequeños. Por ejemplo, si ya se conocen los valores de F31 y F30, se podrá calcular directamente el valor de F32.
Una pertenencia significativa de un problema que se pueda resolver mediante programación dinámica es que debería tener subproblemas sobrepuestos. Esto es lo que distingue a la programación dinámica de la técnica de dividir y conquistar, donde no es necesario almacenar los valores más simples.
Es similar a la recursividad, ya que al calcular los casos base se puede determinar inductivamente el valor final. Este enfoque ascendente funciona bien cuando un nuevo valor dependa solo de valores calculados previamente.
Para cualquier número entero positivo “e” se puede realizar cualquiera de los tres pasos siguientes.
– Restar 1 del número. (e=e-1).
– Si es divisible por 2, se divide entre 2 (si e%2==0, entonces e= e/2).
– Si es divisible por 3, se divide entre 3 (si e%3==0, entonces e= e/3).
Basado en los pasos anteriores, se debe encontrar la cantidad mínima de estos pasos para llevar e a 1. Por ejemplo:
– Si e= 1, resultado: 0.
– Si e= 4, resultado: 2 (4/2= 2/2= 1).
– Cuando e= 7, resultado: 3 (7-1= 6/3= 2/2= 1).
Se podría pensar en elegir siempre el paso que haga que n sea lo más bajo posible y continuar así, hasta que llegue a 1. Sin embargo, se puede observar que esta estrategia no funciona aquí.
Por ejemplo, si e= 10, los pasos serían: 10/2= 5-1= 4/2= 2/2= 1 (4 pasos). Sin embargo, la forma óptima es: 10-1= 9/3= 3/3 = 1 (3 pasos). Por tanto, se deben probar todos los pasos posibles que puedan hacerse para cada valor que se encuentre de n, eligiendo la cantidad mínima de estas posibilidades.
Todo comienza con la recursividad: F(e)= 1 + min{F(e-1), F(e/2), F(e/3)} si e>1, tomando como caso base: F(1)= 0. Teniendo la ecuación de recurrencia, se puede comenzar a codificar la recursión.
Sin embargo, se puede observar que tiene subproblemas sobrepuestos. Además, la solución óptima para una entrada dada depende de la solución óptima de sus subproblemas.
Como en la memorización, donde las soluciones de los subproblemas que se resuelven se van almacenando para usarlos posteriormente. O como en la programación dinámica, se comienza desde abajo, avanzando hasta el e dado. A continuación, ambos códigos:
Memorización

Programación dinámica de abajo hacia arriba

Una de las principales ventajas de usar programación dinámica es que acelera el procesamiento, ya que se usan referencias que fueron previamente calculadas. Como es una técnica de programación recursiva, reduce las líneas de código del programa.
Los algoritmos voraces son similares a la programación dinámica en el sentido que ambos son herramientas para la optimización. Sin embargo, el algoritmo voraz busca una solución óptima en cada paso local. Es decir, busca una elección codiciosa con la esperanza de encontrar un óptimo global.
Por tanto, los algoritmos voraces pueden hacer una suposición que se vea óptima en ese momento, pero que se vuelve costosa en el futuro y no garantiza un óptimo global.
Por otro lado, la programación dinámica encuentra la solución óptima para los subproblemas y luego hace una elección informada combinando los resultados de esos subproblemas para encontrar realmente la solución más óptima.
– Se necesita mucha memoria para almacenar el resultado calculado de cada subproblema, sin poder garantizar que el valor almacenado se utilizará o no.
– Muchas veces, el valor de salida se queda almacenado sin nunca ser utilizado en los siguientes subproblemas durante la ejecución. Esto conlleva a una utilización innecesaria de la memoria.
– En la programación dinámica las funciones se llaman recursivamente. Esto hace que la memoria de pila se mantenga en constante aumento.
Si se tiene memoria limitada para ejecutar el código y no es preocupante la velocidad de procesamiento, se puede usar la recursividad. Por ejemplo, si se está desarrollando una aplicación móvil, la memoria es muy limitada para ejecutar la aplicación.
Si se desea que el programa se ejecute más rápido y no se tienen restricciones de memoria, es preferible utilizar la programación dinámica.
La programación dinámica es un método eficaz para resolver problemas que de otro modo podrían parecer extremadamente difíciles de resolver en un tiempo razonable.
Los algoritmos basados en el paradigma de programación dinámica se utilizan en muchas áreas de las ciencias, incluyendo muchos ejemplos en inteligencia artificial, desde la resolución de problemas de planificación hasta el reconocimiento de voz.
La programación dinámica es bastante efectiva y sirve muy bien para una amplia gama de problemas. Muchos algoritmos se pueden ver como aplicaciones de algoritmos voraces, como:
– Serie de números de Fibonacci.
– Torres de Hanoi.
– Todos los pares de rutas más cortas por Floyd-Warshall.
– Problema de la mochila.
– Programación de proyectos.
– El camino más corto por Dijkstra.
– Control de vuelo y control de robótica.
– Problemas de optimización matemática.
– Tiempo compartido: programar el trabajo para maximizar el uso de la CPU.
Los números de Fibonacci son los números que se encuentran en la secuencia siguiente: 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, etc.
En la terminología matemática, la sucesión Fn de los números de Fibonacci está definida por la fórmula de recurrencia: F(n)= F(n -1) + F(n -2), donde F(0)= 0 y F(1)= 1.
Enfoque de arriba hacia abajo
En este ejemplo, se inicializa con -1 una matriz de búsqueda con todos los valores iniciales. Siempre que se necesite la solución a un subproblema, primero se buscará en esta matriz de búsqueda.
Si allí está el valor calculado, entonces se retornará ese valor. En caso contrario, se calculará el resultado para almacenarlo en la matriz de búsqueda y así poderlo reutilizar más adelante.

Enfoque ascendente
En este caso, para la mismo serie de Fibonacci, se calcula primero f(0), luego f(1), f(2), f(3), y así sucesivamente. Así, se estarán construyendo las soluciones de los subproblemas de abajo hacia arriba.

- Vineet Choudhary (2020). Introduction to Dynamic Programming. Developer Insider.Tomado de: developerinsider.co.
- Alex Allain (2020). Dynamic Programming in C++. C Programming. Tomado de: cprogramming.com.
- After Academy (2020). Idea of Dynamic Programming. Tomado de: afteracademy.com.
- Aniruddha Chaudhari (2019). Dynamic Programming and Recursion | Difference, Advantages with Example. CSE Stack. Tomado de: csestack.org.
- Code Chef (2020). Tutorial For Dynamic Programming. Tomado de: codechef.com.
- Programiz (2020). Dynamic Programming. Tomado de: programiz.com.
