¿Qué es el factor de empaquetamiento?
El factor de empaquetamiento es una fracción que indica cuánto volumen ocupan las partículas, ya sean átomos, iones o moléculas, en el espacio interno de un cristal. Su valor siempre es menor a 1, que viene a ser el 100% del volumen del cristal; más exactamente, la celda unitaria del mismo, la cual es la representación más pequeña del todo el cristal.
Un factor de empaquetamiento del 100% significa que las partículas ocupan el volumen de la celda unitaria en su totalidad. Físicamente es imposible que esto ocurra, porque implicaría, por ejemplo, que los átomos deformaran sus radios y se disolvieran como si fueran un “líquido electrónico”. La geometría de los átomos, esférica por conveniencia, siempre da lugar a espacios vacíos durante su empaquetamiento.

En la definición del factor de empaquetamiento se asume que los átomos consisten en esferas rígidas, como las bolas de chicle o dulce de una máquina dispensadora (imagen superior). Entre las esferas siempre habrá espacios huecos por donde se pueda colar esferas más pequeñas (impurezas o aditivos).
Si aumentamos el factor de empaquetamiento, las esferas se irán apretujando, volviéndose el cristal más compacto y denso; o por otra parte, más deformable, como sucede con los metales maleables y dúctiles.
El factor de empaquetamiento aplica para cualquier tipo de cristal. Sin embargo, su cálculo puede llegar a ser un poco tedioso, por lo que aquí solamente se considerará para cristales atómicos con estructuras simples.
Índice del artículo
- 1 Fórmula del factor de empaquetamiento
- 2 Cúbica simple
- 3 Cúbica centrada en el cuerpo
- 4 Cúbica centrada en las caras
- 5 Hexagonal compacta
- 6 Referencias
El factor de empaquetamiento suele expresarse como porcentajes. Por ejemplo, si su valor es de 40%, quiere decir que las partículas apenas ocupan el 40% del espacio total de la celda unitaria; o lo que es igual a afirmar que el 60% del cristal se encuentra “vacío”.
Lo anterior dicho aclara cuál es la fórmula para calcular este factor:
- FEA= (Volumen de los átomos)/ (Volumen celda unitaria)
Donde FEA significa Factor de Empaquetamiento Atómico, que son los cristales más simples.
El volumen de la celda unitaria depende de sus parámetros (como el largo de sus lados), con los cuales se procede por simple geometría a calcular su volumen. Los átomos, por otro lado, son los que definen dicha celda, por lo que es posible expresar las dimensiones de la misma a partir de los radios atómicos, tal como se verá en próximos apartados.
En lo que respecta al volumen de los átomos, debe considerarse el número total de ellos que está presente en la celda unitaria (1, 2, 3, etc.), así como su geometría esférica. Por lo tanto, la fórmula se modifica un poco:
FEA= (Nº Átomos)(Volumen de átomo)/ (Volumen celda unitaria)
Para calcular FEA hay que determinar entonces Nº, Vátomo y Vcelda unitaria.

La celda unitaria más simple de todas es la cúbica simple. En ella tenemos unas porciones de átomos en cada una de las esquinas. Si vemos, nos fijaremos que el largo a de esta celda es igual a 2r, pues son los átomos los que definen la celda. Entonces, el volumen de la celda unitaria será igual a:
Vcelda unitaria = a3 (volumen de un cubo)
= (2r)3
= 8r3
Mientras, el volumen del átomo será igual a:
Vátomo = (4/3) πr3 (volumen de una esfera)
Cada una de las esquinas es compartida por otras 8 celdas unitarias vecinas. Por lo tanto, tenemos una fracción de 1/8 en cada esquina, y al haber 8 de ellas, nos da igual a 1 átomo por celda unitaria (1/8 x 8 = 1).
El factor de empaquetamiento viene a ser:
FEA= (1)(4/3) πr3 / 8r3
= π/6 ≈ 52%
Es decir, en una celda cúbica simple los átomos ocupan el 52% de todo el volumen del cristal.
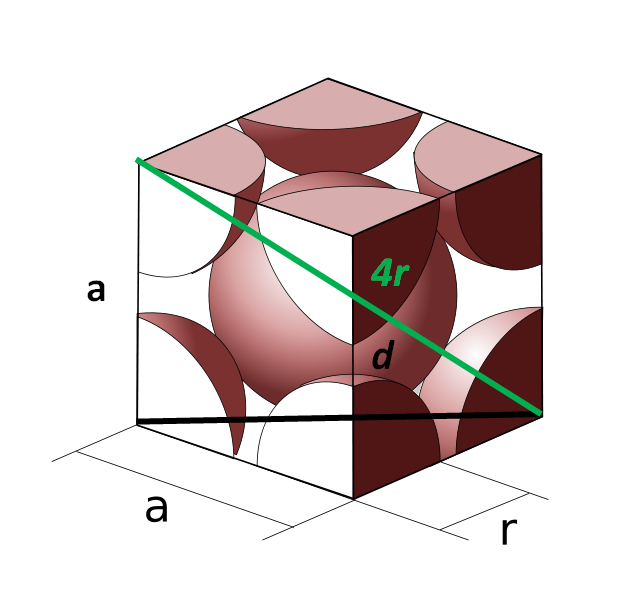
Ahora veamos la celda cúbica centrada en el cuerpo. El lado a ya no puede ser igual a 2r, porque tenemos un espacio vacío entre los dos átomos de las esquinas. Hay pues, que considerar una diagonal d igual a 4r (color verde) que atraviese la celda por el centro y toque las esquinas opuestas, y otra diagonal d de la cara (color negro).
Los lados a, d y 4r dibujan un triángulo rectángulo al cual podemos aplicar trigonometría para calcular cuál es el valor de a:
(4r)2 = d2 + a2
Pero por otro lado, en la base de la celda unitaria tenemos otro triángulo (a, a y d) al cual le podemos calcular la hipotenusa:
d2 = a2 + a2
= 2a2
Sustituyendo entonces tendremos:
(4r)2 = (2a2) + a2
(4r)2 = 3a2
a = (4/√3)r
El Vcelda unitaria es igual a:
Vcelda unitaria = a3
= ((4/√3)r)3
Nótese que respecto al número de átomos tenemos 1 átomo dentro de esta celda, siguiendo la misma deducción realizada para la celda cúbica simple, y otro átomo adicional que se localiza en el centro de la celda. Así, hay un total de 2 átomos por cada celda cúbica centrada en el cuerpo.
El factor de empaquetamiento viene a ser entonces:
FEA= (2)(4/3) πr3 / ((4/√3)r)3
= (√3/8) π ≈ 68%
Es decir, que en una celda cúbica centrada en el cuerpo, el 68% del volumen del cristal se encuentra ocupado por los átomos. En consecuencia, este arreglo cristalino es más compacto (o denso) que el cúbico simple.
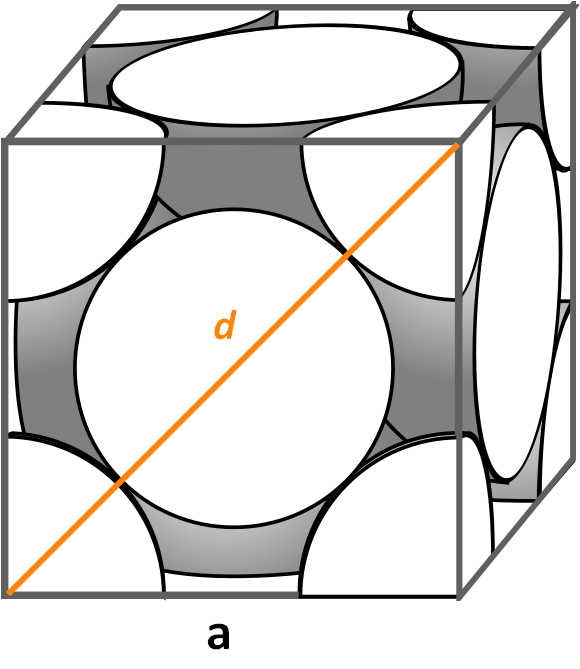
Veamos ahora la celda unitaria cúbica centrada en las caras, muy común en sinfines de sales inorgánicas y algunos metales, como el oro y la plata. Para determinar su factor de empaquetamiento debemos empezar, siguiendo los ejemplos anteriores, por encontrar cuál es el volumen de su celda unitaria. Es necesario pues calcular nuevamente el lado a y así el volumen del cubo a3.
Esta vez el procedimiento es más fácil y directo, pues tenemos una diagonal d frontal que, junto con los lados a, forman un triángulo rectángulo al cual podemos aplicar trigonometría:
d2 = a2 + a2
= 2a2
Despejando a tendremos:
a = d/√2
Pero, visualmente nos fijamos que d es igual a 4r, por lo que hacemos una sustitución:
a = 4r/√2
= 2r 21-1/2
= (2√2)r
Siendo Vcelda unitaria igual a:
a3 = ((2√2)r)3
= (16√2) r3
Respecto al número de átomos por celda, tenemos otra vez ocho porciones de un átomo en cada esquina, y además, una mitad de átomo por cada una de las seis caras, la cual es compartida por otra celda vecina. Por lo tanto, el número de átomos es igual a:
Nº átomos = 1/8(8) + 1/2(6) = 1 + 3 = 4
Teniendo que hay 4 átomos en cada celda cúbica centrada en las caras, y también su volumen, el cual es igual a (16√2) r3, podemos calcular entonces el factor de empaquetamiento:
FEA= (Nº Átomos)(Volumen de átomo)/ (Volumen celda unitaria)
= (4)(4/3) πr3 / (16√2) r3
= π/(3√2) ≈ 74%
Nótese que esta celda es todavía más compacta que las anteriores: el 74% del volumen total de la celda está ocupado por átomos. En un cristal perfecto y puro, esto equivaldría a decir que el 26% de su volumen está disponible para alojar otros átomos huéspedes.
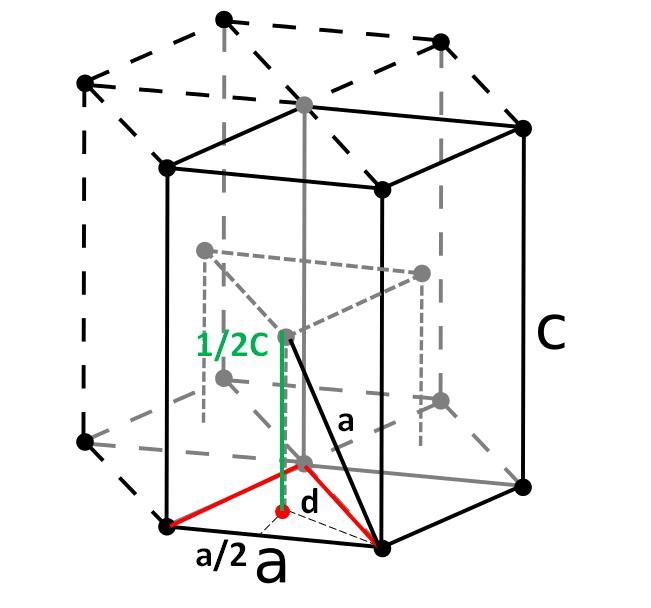
Por último, entre las celdas unitarias más simples y compactas tenemos la hexagonal compacta. A diferencia de las anteriores, el cálculo de su volumen es un poco más engorroso. Como puede verse, no es cúbica, por lo que tiene dos parámetros a y c, siendo este último la altura de la celda.
La celda hexagonal puede descomponerse en tres celdas romboédricas, y a partir de una de ellas se procederá a calcular a y c. El lado a, aunque no sea tan evidente en la imagen de arriba, es igual a 2r. Para calcular c, en cambio, utilizamos el triángulo y el punto rojos producto del prisma triangular interno de la misma celda.
Necesitamos calcular la distancia d para poder determinar cuánto vale c. En el piso el triángulo rojo es equilátero, con un ángulo de 60º. Pero si se considera otro triángulo rectángulo interno con lados a/2 y d, y un ángulo de 30º (la mitad), entonces por trigonometría podremos determinar d:
Cos(30º) = (a/2) / d
d = a/√3
Y ahora consideramos el triángulo rectángulo compuesto por los lados c/2 (verde), a (negro) y d (punteado):
a2 = (a/√3)2 + (c/2)2
Despejando c tendríamos:
c = √(8/3) a
Y sustituyendo a por 2r:
c = √(8/3) (2r)
= √(4·2/3) (2r)
= 4√(2/3) r
Para determinar el volumen de la celda hexagonal hay que multiplicar el área del hexágono por su altura. Sabiendo que los triángulos equiláteros tienen lados a, se calcula su altura h. Así, hallando el área de un triángulo, el cual es para este caso √3/4a2, multiplicamos este valor por 6 para obtener el área del hexágono: 3(√3/2)a2
El volumen por tanto es:
Vcelda unitaria = Área hexágono x Altura
= 3(√3/2)a2 x 4√(2/3) r
Y sustituyendo una vez más a por 2r:
Vcelda unitaria = 3(√3/2) (2r)2 x 4√(2/3) r
= 24√2 r3
En la celda hexagonal hay 12 átomos en las esquinas, los cuales tienen 1/6 de sus volúmenes en el interior. Asimismo, hay 3 átomos internos cuyos volúmenes están completos, y otros 2 átomos sobre las caras superior e inferior cuya mitad de sus volúmenes están dentro de la celda.
Por lo tanto, el número de átomos es igual a:
Nº átomo = 1/6 (12) + 1(3) + 1/2(2) = 6 átomos
Y el factor de empaquetamiento viene a ser finalmente:
FEA= (Nº Átomos)(Volumen de átomo)/ (Volumen celda unitaria)
= (6)(4/3) πr3 / 24√2 r3
= π/(3√2) ≈ 74%
Nótese que el factor de compartimiento para la celda hexagonal es el mismo que para la celda cúbica centrada en las caras. Es decir, ambas son igual de compactas.
- C. Barry Carter & M. Grant Norton. (2007). Ceramic Materials Science and Engineering. Springer.
- Shiver & Atkins. (2008). Química Inorgánica. (Cuarta edición). Mc Graw Hill.
- Whitten, Davis, Peck & Stanley. (2008). Química. (8va ed.). CENGAGE Learning.
- Wikipedia. (2021). Atomic packing factor. Recuperado de: en.wikipedia.org
- Brandon. (2021). What is Atomic Packing Factor (and How to Calculate it for SC, BCC, FCC, and HCP)? Materials Science & Engineering Student. Recuperado de: msestudent.com
