Prisma pentagonal: características, partes, vértices, aristas, volumen
Un prisma pentagonal es una figura geométrica tridimensional cuyas bases, idénticas, tienen forma de pentágono, y además posee un total de 5 caras en forma de paralelogramo.
Si las caras son rectangulares se dice que es un prisma pentagonal recto, mientras que si las aristas están inclinadas respecto a las bases, entonces es un prisma pentagonal oblicuo. En la siguiente imagen hay un ejemplo de cada uno.

El pentágono de la base puede ser regular si sus cinco lados tienen la misma medida, así como los ángulos internos, de lo contrario es un pentágono irregular. Si la base del prisma es regular, se trata de prisma pentagonal regular. De lo contrario es un prisma pentagonal irregular.

El prisma pentagonal es una estructura armoniosa que se usa en arquitectura y diseño de objetos, como por ejemplo el moderno edificio que se muestra en la figura superior. Los ventanales en forma de pentágono irregular forman la base de los prismas.
Índice del artículo
- 1 Características del prisma pentagonal
- 2 Elementos del prisma pentagonal
- 3 ¿Cuántos vértices tiene un prisma pentagonal?
- 4 ¿Cuántas aristas tiene un prisma pentagonal?
- 5 ¿Cómo sacar el volumen de un prisma pentagonal?
- 6 Referencias

-Es una figura geométrica tridimensional, las superficies que la componen encierran un determinado volumen.
-Sus bases son pentágonos y sus caras laterales pueden ser rectángulos o paralelogramos.
-Tiene vértices -las esquinas del prisma- y aristas -bordes u orillas-.
-Si las aristas que unen las bases son perpendiculares a ellas, el prisma es recto, y si son inclinadas, el prisma es oblicuo.
-Cuando la base es un pentágono cuyos ángulos internos son menores de 180º, el prisma es convexo, pero si uno o más ángulos internos es mayor de 180º, es un prisma cóncavo.

–Bases: tiene dos bases pentagonales y congruentes –sus medidas son las mismas-, ya sea regulares o irregulares.
–Caras: un prisma pentagonal tiene un total de 7 caras: las dos bases pentagonales y los cinco paralelogramos que conforman los laterales.
–Arista: segmento que une dos bases, mostrado en color rojo en la figura 3 o bien el que une dos lados.
–Altura: distancia entre las caras. Si el prisma es recto, esta distancia coincide con el tamaño de la arista.
–Vértice: punto en común entre una base y dos caras laterales.
La figura inferior muestra un prisma pentagonal recto de base regular, en el cual los segmentos que forman la base tienen igual medida, llamada a.
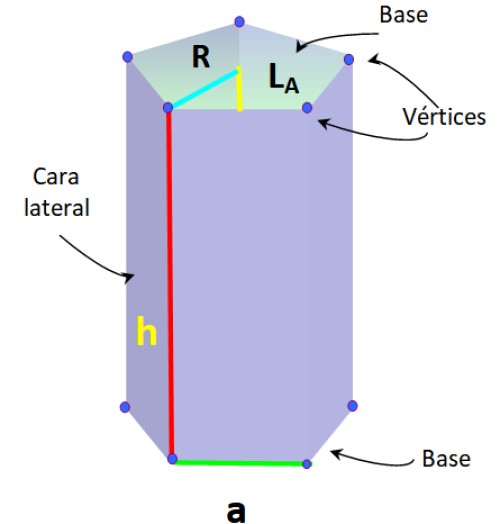
Este tipo de prisma cuenta además con los siguientes elementos, propios del pentágono regular:
–Radio R: distancia entre el centro del pentágono y uno de los vértices.
–Apotema LA: segmento que une al centro con el punto medio de uno de los lados del pentágono.
En un pentágono hay 5 vértices y como el prisma pentagonal tiene dos pentágonos como bases, este cuerpo tiene en total 10 vértices.
Se puede calcular el número de aristas para cuerpos geométricos con caras planas, como los prismas, mediante el teorema de Euler para poliedros convexos. Leonhard Euler (1707-1783) es uno de los matemáticos y físicos más grandes de la historia.
El teorema establece una relación entre el número de caras, al cual llamaremos C, la cantidad de vértices V y el total de aristas A como sigue:
C+V = A+2
Para el prisma pentagonal tenemos: C = 7 y V = 10. Despejando A, el número de aristas:
A = C+V-2
Sustituyendo valores:
A = 7 + 10 – 2 = 15
Un prisma pentagonal tiene 15 aristas.
El volumen del prisma pentagonal mide el espacio encerrado por los lados y las bases. Se trata de una cantidad positiva que se calcula mediante la siguiente propiedad:
Cualquier plano que corte al prisma perpendicularmente a sus aristas, genera una intersección con la misma forma que la base, es decir, un pentágono de las mismas dimensiones.
Por lo tanto, el volumen del prisma pentagonal es el producto del área de la base y la altura del prisma.
Sea AB el área de la base pentagonal y h la altura del prisma, entonces el volumen V es:
V = AB x h
Esta fórmula es de carácter general, siendo válida para cualquier prisma, ya sea regular o irregular, recto u oblicuo.
El volumen de un prisma siempre viene en unidades de longitud elevadas al cubo. Si la longitud de los lados y la altura del prisma vienen dadas en metros, entonces el volumen se expresa en m3, que se lee “metros cúbicos”. Otras unidades incluyen cm3, km3, pulgadas3 y más.
En el prisma pentagonal regular las bases son pentágonos regulares, lo cual significa que el lado y los ángulos internos son iguales. Dada la simetría del cuerpo, el área del pentágono y por consiguiente el volumen se calculan fácilmente de varias maneras:
Conociendo la altura y la medida del lado
Sea a la medida del lado de la base pentagonal. En ese caso el área se calcula mediante:

Por lo tanto el volumen del prisma pentagonal regular de altura h es:
V = 1.72048 a2⋅ h
Conociendo la altura y la medida del radio
Cuando se conoce el radio R de la base pentagonal, se puede emplear esta otra ecuación para el área de la base:
A = (5/2)R2⋅ sen 72º
De esta manera el volumen del prisma pentagonal viene dado por:
V = (5/2)R2 ⋅ h ⋅ sen 72º
Donde h es la altura del prisma
Conociendo la altura, la medida de la apotema y el valor del perímetro
El área de la base pentagonal se puede calcular si se conoce su perímetro P, el cual es simplemente la suma de los lados, así como la medida de la apotema LA:
A = P. LA / 2
Multiplicando esta expresión por el valor de la altura h, tenemos el volumen del prisma:
V = P. LA .h / 2
La fórmula dada al comienzo es válida aún cuando la base del prisma sea un pentágono irregular:
V = AB x h
Para calcular el área de la base se emplean diversos métodos, por ejemplo:
-Método de la triangulación, que consiste en dividir el pentágono en triángulos y cuadriláteros, cuyas respectivas áreas se calculan fácilmente. El área del pentágono será la suma de las áreas de estas figuras más simples.
-Método de los determinantes de Gauss, para el cual hay que conocer los vértices de la figura.
Una vez determinado el valor del área, se multiplica por la altura del prisma para obtener el volumen.
- Alexander, D. 2013. Geometría. 5ta. Edición. Cengage Learning.
- Math Open Reference. Area of a polygon. Recuperado de: mathopenref.com.
- Universo Fórmulas. Teorema de Euler para poliedros. Recuperado de: universoformulas.com.
- Universo Fórmulas. Área de un pentágono regular. Recuperado de: universoformulas.com.
- Wikipedia. Prisma. Recuperado de: es.wikipedia.com.
- Wikipedia. Prisma pentagonal. Recuperado de: es.wikipedia.com.
