Movimiento circular uniforme (M.C.U.): fórmulas, características
Una partícula tiene movimiento circularuniforme (M.C.U.) cuando su trayectoria es una circunferencia y además la recorre con rapidez constante. Numerosos objetos como piezas de maquinarias y motores, por ejemplo, tienen esta clase de movimiento, entre los que destacan los discos duros de las computadoras, la aspas de los ventiladores, ejes y muchísimas cosas más.
El movimiento circular uniforme también es una buena aproximación para el movimiento de algunos cuerpos celestes como la Tierra. Realmente la órbita terrestre es elíptica, conforme lo señalan las leyes de Kepler. No obstante, la excentricidad de la órbita es pequeña y como primera aproximación se puede considerar circular, lo cual simplifica algunos cálculos, como por ejemplo el de encontrar la velocidad de la Tierra cuando se traslada alrededor del Sol.
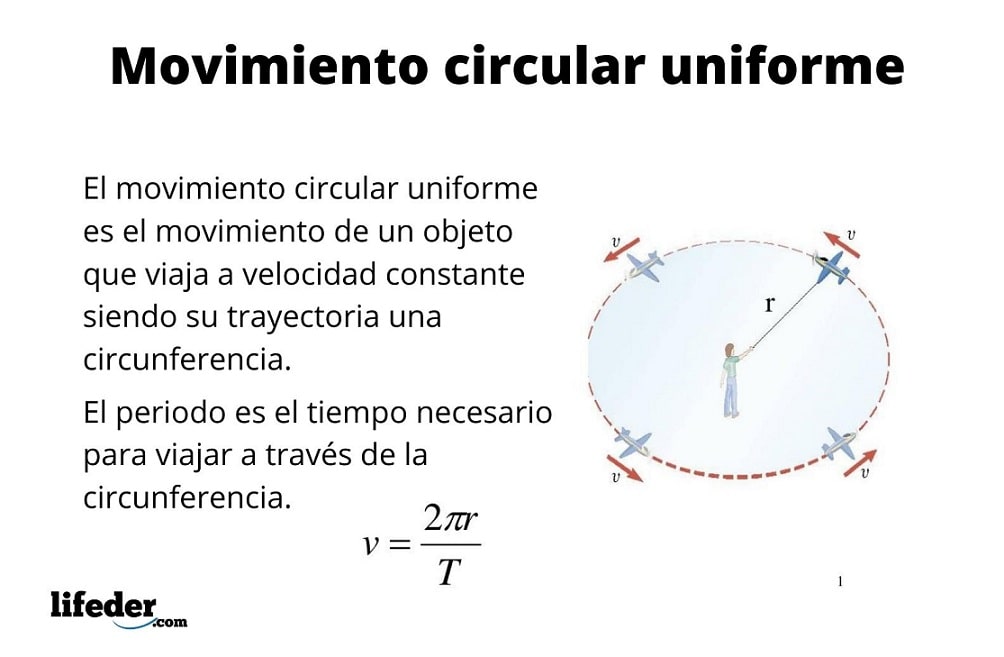
En la descripción del movimiento circular uniforme se utilizan los mismos parámetros que en el movimiento rectilíneo, a saber: posición, desplazamiento, tiempo, velocidad y aceleración.
¿Aceleración? Sí, en efecto, el movimiento circular uniforme es acelerado, aun cuando su rapidez v sea constante. Ello se debe a que la velocidad v, que es un vector y por eso va en negrita, cambia continuamente su dirección a medida que el objeto o la partícula rotan. Cualquier cambio en v es producido por una aceleración, que como se verá, está dirigida hacia el centro de la trayectoria circular.
El movimiento circular uniforme es un movimiento en el plano xy, por lo tanto es un movimiento en dos dimensiones. Sin embargo, es posible expresarlo más cómodamente mediante el ángulo θ que barre la partícula, medido respecto al eje horizontal u otro eje de referencia adecuado.
Incluso si se trata de un objeto extendido, sus partículas barren siempre el mismo ángulo, aunque tengan diferentes coordenadas (x,y).
Índice del artículo
- 1 Características del movimiento circular uniforme
- 2 Fórmulas del movimiento circular uniforme
- 3 Ejemplos de movimiento circular uniforme
- 4 Ejercicio resuelto
- 5 Referencias
Se pueden resumir las características del movimiento circular uniforme como sigue:
-La trayectoria es una circunferencia, por lo tanto se trata de un movimiento en el plano.
-La rapidez v es constante, pero la velocidad v no, porque continuamente cambia de dirección y sentido para acomodarse al giro del móvil.
-El vector velocidad v siempre es tangencial a la circunferencia y perpendicular a la dirección radial.
-La velocidad angular ω es constante.
-A pesar de ser uniforme, existe una aceleración para explicar estos cambios en la dirección de la velocidad. Dicha aceleración es la aceleración centrípeta.
-La aceleración centrípeta y la velocidad son perpendiculares entre sí.
-Es un movimiento periódico o repetitivo, por lo tanto se definen para él las magnitudes período y frecuencia.
En este esquema hay una partícula P dando vueltas en sentido antihorario con MCU, según la dirección y el sentido del vector velocidad v dibujado.
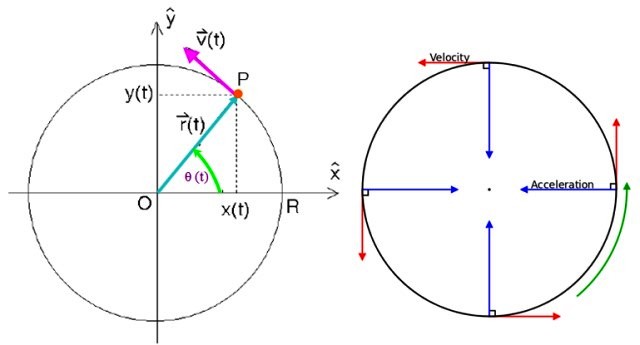
Para especificar el vector de posición es necesario contar con un punto de referencia y el punto idóneo es el centro de la circunferencia O que coincide con el centro del sistema de coordenadas cartesianas en el plano xy.
Se denota como r(t) y está dirigido desde el origen hasta el punto P donde se encuentra la partícula. En un instante dado t, en coordenadas cartesianas, se escribe como:
r (t) = x (t) i + y (t) j
Donde i y j son los vectores unitarios perpendiculares en las direcciones x e y respectivamente. Del gráfico se observa que el módulo del vector r (t) siempre vale R, el radio de la circunferencia. Si θ es el ángulo que forma r con el eje horizontal, la posición también equivale a:
r (t) =[Rcos θ(t)] i +[Rsen θ(t)] j
El ángulo que forma r (t) con el eje horizontal es un ángulo central y su valor es:
θ = s/R
Donde s es el arco de circunferencia recorrido y R el radio. Dicho ángulo θ es una función del tiempo, por lo que se puede escribir θ = θ (t), llamada posición angular.
Ya que la rapidez es constante, la partícula describe ángulos iguales en tiempos iguales y en analogía con el movimiento rectilíneo uniforme, se escribe:
θ = θ (t)= θo + ωt
Aquí θo es el ángulo inicial medido en radianes respecto al eje de referencia, puede ser 0 o cualquier valor y ω es la rapidez angular.
La velocidad angular es la primera derivada de la posición angular y se denota como ω. Su valor es constante para el movimiento circular uniforme, ya que se barren ángulos iguales en tiempos iguales. En otras palabras:
Las unidades de la rapidez lineal en el movimiento circular uniforme son las mismas que para los movimientos lineales: m/s (en el Sistema Internacional SI), km/h, cm/s y otras.
En la siguiente figura hay una partícula que se mueve en sentido horario de la circunferencia con rapidez constante. Esto quiere decir que el vector velocidad tiene el mismo módulo siempre, pero va cambiando de dirección para acomodarse a la circunferencia.
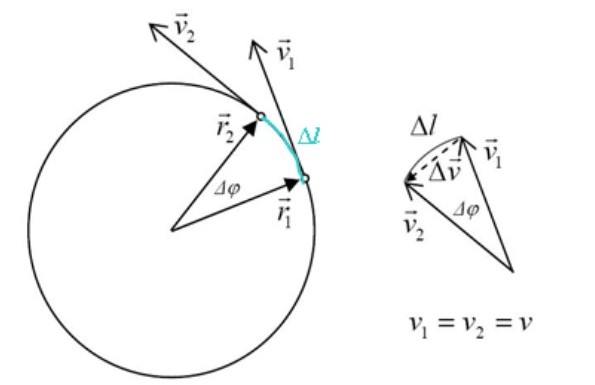
Cualquier cambio en la velocidad da lugar a una aceleración, que por definición es:
El triángulo formado por v2, v1 y Δv es semejante al triángulo de lados r2, r1 y Δl, siendo Δφ el ángulo central. Las magnitudes de r2 y r1 son iguales, así que:
r2 = r1 = r
Entonces, de ambos triángulos se tienen estas relaciones para el ángulo:
Δφ = Δr / r ; Δφ = Δv / v
Las negritas no son necesarias, ya que la medida del ángulo depende de las magnitudes de dichos vectores. Igualando las expresiones anteriores se deduce que:
Como el movimiento circular es repetitivo, se define el período T del mismo como el tiempo que tarda el móvil en dar una vuelta completa. Ya que la longitud de la circunferencia de radio R es 2πR, el ángulo barrido en radianes al dar la vuelta completa es 2π radianes y se tarda un tiempo T, la velocidad angular es:
ω = 2π / T
T = 2π / ω
El período del movimiento circular uniforme se mide en segundos en el Sistema Internacional.
Por su parte, la frecuencia f es el número de vueltas por unidad de tiempo y es el recíproco o inverso del período:
f = n /t = 1 /T
La unidad de la frecuencia en el Sistema Internacional es s-1.
Muchos objetos rotan para producir efectos diversos: ruedas, discos y turbinas. Una vez que se alcanza la velocidad de funcionamiento, la rotación suele llevarse a cabo con rapidez constante. El movimiento circular es tan común en la vida diaria que casi nunca se piensa en él, por eso acá hay algunos ejemplos cercanos que lo ilustran muy bien:
La Tierra y los demás planetas del Sistema Solar se mueven en trayectorias elípticas de pequeña excentricidad, excepto Mercurio, lo que significa que en primera aproximación, se puede suponer que su movimiento es circular uniforme.
Con ello se tiene una buena idea de la velocidad de traslación alrededor del Sol, ya que en el caso de la Tierra se conoce el período del movimiento: un año o 365 días.

Las partículas que giran en el borde de un tocadiscos antiguo o el aspa de un ventilador, siguen un movimiento circular uniforme, una vez que el aparato alcanza su velocidad de reproducción.

El telescopio espacial Hubble da vueltas alrededor de la Tierra a unos 7550 m/s aproximadamente.
Las lavadoras llevan a cabo un proceso de centrifugado para exprimir la ropa, que consiste en hacer rotar el tambor contenedor a alta velocidad. Las secadoras también giran durante un lapso de tiempo con movimiento circular uniforme.
La centrifugación también se emplea en laboratorios para separar compuestos, por ejemplo, y separar de esta manera sus constituyentes por diferencia de densidades. Siempre que se habla de centrifugación, hay un movimiento circular que es uniforme, al menos por un tiempo.
Muchas regaderas de jardín dan vueltas con rapidez constante para que el terreno se riegue de forma pareja.

En el lanzamiento de martillo por ejemplo, que es una disciplina olímpica, el atleta hace girar con fuerza una bola de metal mediante un cable de acero unido a la empuñadura. El objetivo es enviar la bola lo más lejos posible, pero sin salirse de un área determinada.
Una partícula se mueve en una circunferencia de radio 2m con una rapidez constante v = 8 m/s, en el sentido contrario al reloj. Inicialmente la partícula se hallaba en r = +2 j m. Calcular:
a) La velocidad angular ω
b) Su posición angular θ (t)
c) El período del movimiento
d) La aceleración centrípeta.
e) Posición de la partícula luego de transcurrir t = π/4 s
Solución a
De la fórmula v = Rω se deduce que:
ω = v/R = (8 m/s) / 2m = 4rad∙s-1
Solución b
Tomando como eje de referencia al eje x positivo, la partícula inicialmente está a 90º = π/2 radianes respecto a dicho eje, ya que el enunciado dice que la posición inicial es +2 j m, o sea que la partícula se encuentra en y = 2m cuando se empieza a seguir el movimiento.
θ = θ (t)= θo + ωt = π/2 + 4t
Solución c
T = 2π / ω = 2π / 4 s = 0.5 π s
Solución d
a = v2 / R = (8 m/s)2 / 2 m = 32 m/s2
Solución e
θ (t) = π/2 + 4t → θ (π/4) = π/2 + 4∙(π/4) = 3π/2 radianes
Esto significa que al cabo de ese tiempo, la partícula se encuentra en la posición y = -2m j. Tiene sentido porque t = π/4 s es la mitad del período, por lo tanto la partícula recorrió un ángulo de 180º en sentido antihorario desde su posición inicial y tiene que encontrarse justo en la posición opuesta.
- Figueroa, D. (2005). Serie: Física para Ciencias e Ingeniería. Volumen 1. Cinemática. Editado por Douglas Figueroa (USB).
- Giambattista, A. 2010. Physics. 2nd. Ed. McGraw Hill.
- Sears, Zemansky. 2016. University Physics with Modern Physics. 14th. Ed. Volume 1. Pearson.
- Serway, R., Jewett, J. (2008). Física para Ciencias e Ingeniería. Volumen 1. 7ma. Ed. Cengage Learning.
- Zapata, F. Movimiento Circular. Recuperado de: francesphysics.blogspot.com.
