Hipercubo: definición, dimensiones, coordenadas, desdoblado
Un hipercubo es un cubo de dimensión n. El caso particular del hipercubo de dimensión cuatro se llama teseracto. Un hipercubo o n-cubo consta de segmentos rectos, todos de igual longitud que son ortogonales en sus vértices.
Los seres humanos percibimos el espacio tridimensional: ancho, alto y profundidad, pero no nos es posible visualizar un hipercubo de dimensión mayor que 3.
Como máximo podemos hacer proyecciones del mismo en el espacio tridimensional para representarlo, en forma semejante a como proyectamos un cubo en un plano para representarlo.
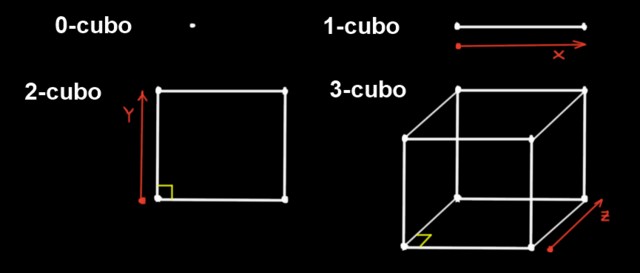
En la dimensión 0 la única figura es el punto, por lo que un 0-cubo es un punto. Un 1-cubo es un segmento recto, el cual se forma al desplazar un punto en una dirección una distancia a.
Por su parte un 2-cubo es un cuadrado. Se construye desplazando el 1-cubo (el segmento de largo a) en la dirección y, la cual es ortogonal a la dirección x, una distancia a.
El 3-cubo es el cubo común. Se construye a partir del cuadrado desplazando el mismo en la tercera dirección (z), la cual es ortogonal a las direcciones x e y, una distancia a.
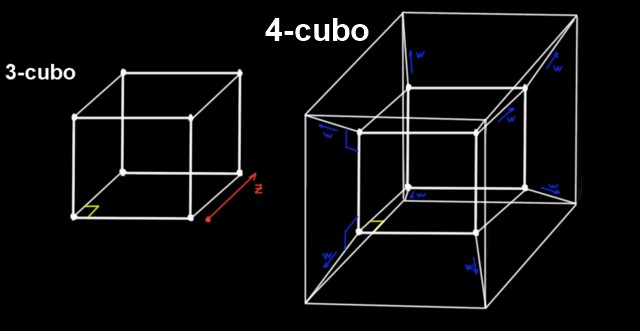
El 4-cubo es el teseracto, el cual se construye a partir de un 3-cubo desplazando el mismo ortogonalmente, una distancia a, hacia una cuarta dimensión (o cuarta dirección), la cual no podemos percibir.
Un teseracto tiene todos sus ángulos rectos, tiene 16 vértices y todas sus aristas (18 en total) tienen la misma longitud a.
Si la longitud de las aristas de un n-cubo o hipercubo de dimensión n es 1, entonces se trata de un hipercubo unitario, en el cual la diagonal más larga mide √n.

Índice del artículo
Las dimensiones son los grados de libertad, o las posibles direcciones en las que un objeto puede trasladarse.
En dimensión 0 no hay ninguna posibilidad de trasladarse y el único objeto geométrico posible es el punto.
Una dimensión en el espacio euclidiano se representa por una recta orientada o eje que define dicha dimensión, llamado el eje X. La separación entre dos puntos A y B es la distancia euclidiana:
d=√[(xa – xb)2].
En dos dimensiones el espacio se representa por dos rectas orientadas ortogonales entre sí, llamadas eje X y eje Y.
La posición de un punto cualquiera en este espacio bidimensional está dada por su par de coordenadas cartesianas (x, y) y la distancia entre dos puntos A y B cualesquiera será:
d =√[(xa – xb)2 + (ya – yb)2]
Porque se trata de un espacio donde se cumple la geometría de Euclides.
El espacio tridimensional es el espacio en que nos movemos. Tiene tres direcciones: ancho, alto y profundidad.
En una habitación vacía las esquinas perpendiculares entre sí dan estas tres direcciones y a cada una podemos asociar un eje: X, Y , Z.
Este espacio también es euclidiano y la distancia entre dos puntos A y B se calcula de la siguiente manera:
d =√[(xa – xb)2 + (ya – yb)2 + (za – zb)2]
Los seres humanos no podemos percibir más que tres dimensiones espaciales (o euclídeas).
Sin embargo, desde el punto de vista estrictamente matemático es posible definir un espacio euclídeo de n-dimensiones.
En este espacio un punto tiene coordenadas: (x1, x2, x3, ….., xn) y la distancia entre dos puntos es:
d =√[(x1a – x1b)2 + (x2a – x2b)2 + ….. + (xna – xnb)2].
La cuarta dimensión y el tiempo
Efectivamente, en teoría de relatividad el tiempo se trata como una dimensión más y se le asocia una coordenada.
Pero hay que aclarar que esa coordenada asociada al tiempo es un número imaginario. Por lo tanto la separación de dos puntos o eventos en el espacio-tiempo no es euclidiana, sino que sigue la métrica de Lorentz.
Un hipercubo de cuatro dimensiones (el teseracto) no vive en el espacio-tiempo, pertenece a un hiper-espacio euclídeo de cuatro dimensiones.

Las coordenadas de los vértices de un n-cubo centrado en el origen se consiguen al hacer todas las permutaciones posibles de la siguiente expresión:
(a/2)(±1, ±1, ±1, …., ±1)
Donde a es la longitud de la arista.
-El volumen de un n-cubo de arista a es: (a/2)n (2n) = an.
-La diagonal más larga es la distancia entre vértices opuestos.
-Los siguientes son vértices opuestos en un cuadrado: (-1, -1) y (+1, +1).
-Y en un cubo: (-1, -1, -1) y (+1, +1, +1).
-La diagonal más larga de un n-cubo mide:
d=√[1 -(-1))2 + …..+ (1 -(-1))2] = √[n 22] = 2√n
En este caso se supuso que el lado es a=2. Para un n-cubo de lado a cualquiera quedará:
d = a√n.
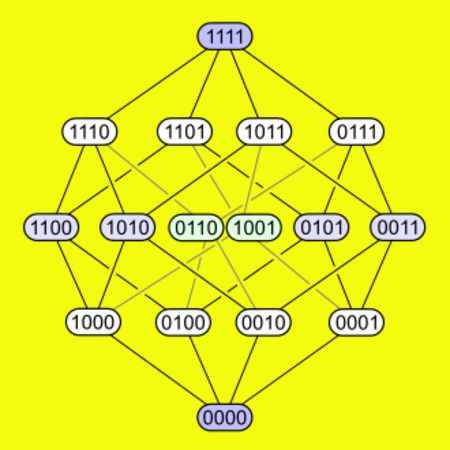
-Un teseracto tiene cada uno de sus 16 vértices conectado a cuatro aristas. La siguiente figura muestra cómo se conectan los vértices en un teseracto.
Un figura geométrica regular, por ejemplo un poliedro, puede desdoblarse en varias figuras de dimensionalidad menor.
En el caso de un 2-cubo (un cuadrado) puede desdoblarse en cuatro segmentos, es decir cuatro 1-cubo.
Similarmente un 3-cubo puede desdoblarse en seis 2-cubo.

Un 4-cubo (teseracto) puede desdoblarse en ocho 3-cubo.
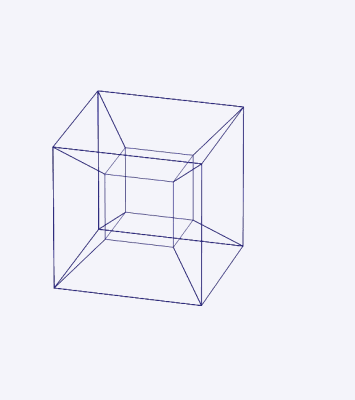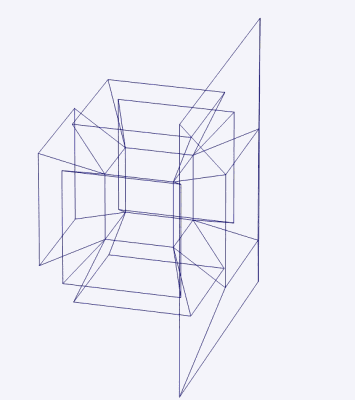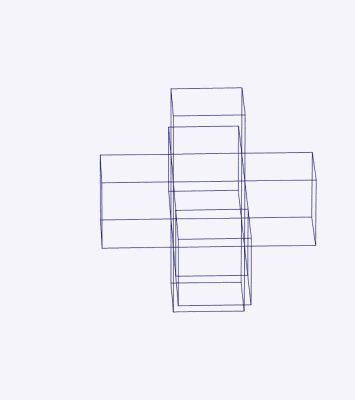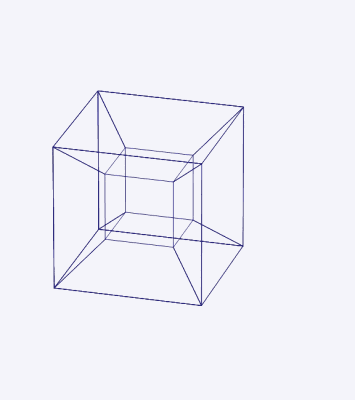
La siguiente animación muestra el desdoble de un teseracto.

- Cultura científica. Hipercubo, visualizando la cuarta dimensión. Recuperado de: culturacientifica.com
- Epsilones. Hipercubo tetradimensional o tesseract. Recuperado de: epsilones.com
- Perez R, Aguilera A. Un método para la obtención de un teseracto a partir del desenvolvimiento de un hipercubo (4D). Recuperado de: researchgate.net
- Wikilibros. Matemáticas, Poliedros, Hipercubos. Recuperado de: es.wikibooks.org
- Wikipedia. Hypercube. Recuperado de: en.wikipedia.com
- Wikipedia. Tesseract. Recuperado de: en.wikipedia.com
