Muestreo estratificado: qué es, tipos, ventajas y desventajas
El muestreo estratificado, o estratificación, es un método de muestreo que implica la división de una población en subgrupos más pequeños, conocidos como estratos. A su vez, estos estratos se forman en función de los atributos o características compartidos de los miembros, como ingresos o nivel educativo.
Se utiliza para resaltar las diferencias entre los grupos de una población, a diferencia del muestreo simple, que trata a todos los miembros de una población como iguales, con la misma probabilidad de ser muestreados.

El objetivo es mejorar la precisión de la muestra reduciendo el error de muestreo. Puede producir una media ponderada con menos variabilidad que la media aritmética de una muestra simple de la población.
La estratificación es el proceso de fragmentar antes de un muestreo a los miembros de una población en subconjuntos homogéneos. Mediante los estratos se define una distribución de la población.
Es decir, debe ser colectivamente exhaustivo y mutuamente excluyente, por lo que se debe asignar un solo estrato a cada elemento de la población. Luego se aplica un muestreo sistemático o simple dentro de cada estrato.
Índice del artículo
- 1 Consideraciones importantes
- 2 ¿En qué consiste el muestreo estratificado?
- 3 Tipos
- 4 Ventajas y desventajas
- 5 Ejemplo
- 6 Referencias
Es importante notar que los estratos no deben yuxtaponerse. Tener subgrupos sobrepuestos otorgará a algunas personas mayor posibilidad de ser seleccionadas como sujetos. Esto entorpece totalmente la noción de muestreo estratificado como un prototipo de muestreo.
Es igualmente importante que el investigador deba utilizar un muestreo simple dentro de los diferentes estratos.
Los estratos más comunes utilizados en el muestreo estratificado son la edad, el género, el nivel socioeconómico, la religión, la nacionalidad y el nivel educativo.
Al completar el análisis en un grupo de entidades con características similares, un investigador puede encontrar que el tamaño de la población es demasiado grande para concluir dicha investigación.
Para ahorrar tiempo y dinero, se puede adoptar una perspectiva más factible seleccionando un pequeño grupo de la población. Este grupo pequeño se denomina tamaño de la muestra, que es un subconjunto de la población utilizado para representar a toda la población.
Se puede seleccionar una muestra de una población de varias maneras, una de las cuales es con el muestreo estratificado. Esto implica dividir a la población total en grupos homogéneos llamados estratos. Luego se seleccionan muestras aleatorias de cada estrato.
– Dividir la población en subgrupos o estratos más pequeños, según los atributos y características compartidos por los miembros.
– Tomar una muestra aleatoria de cada estrato en un número que sea proporcional al tamaño del estrato.
– Agrupar los subconjuntos de estratos para formar una muestra aleatoria.
– Realizar el análisis.
Por ejemplo, consideremos un investigador que quisiera saber la cantidad de estudiantes de administración que recibieron una oferta de trabajo dentro de los tres meses siguientes a su graduación en 2018. Pronto descubrirá que hubo casi 200.000 graduados de administración ese año.
Podría decidir tomar simplemente una muestra aleatoria de 5.000 graduados y realizar la encuesta. Mejor aún, podría dividir la población en estratos y tomar una muestra aleatoria sobre esos estratos.
Para hacer esto, crearía grupos de población basados en edad, raza, nacionalidad o antecedentes profesionales.
Se tomaría una muestra aleatoria de cada estrato, en proporción al tamaño del estrato con respecto a la población total. Estos subconjuntos se agruparían para formar una muestra.
En este tipo, el tamaño de la muestra para cada estrato es proporcional al tamaño de la población del estrato cuando se compara con la población total. Esto significa que cada estrato tiene la misma proporción de muestreo.
Cuando se selecciona una característica de los individuos para definir los estratos, los subgrupos resultantes son a menudo de diferentes tamaños.
Por ejemplo, se quiere estudiar el porcentaje de la población mexicana que fuma, y se decide que la edad sería un buen criterio para estratificar porque se cree que los hábitos de fumar pueden variar significativamente según la edad. Se definen tres estratos:
– Menor de 20 años.
– Entre 20 y 44.
– Mayor de 44.
Cuando se divide a la población de México en estos tres estratos, no se espera que los tres grupos sean del mismo tamaño. De hecho, los datos reales confirman esto:
– El estrato 1: 42.4 millones (41.0%).
– Estrato 2: 37.6 millones (36.3%).
– Estrato 3: 23.5 millones (22.7%).
Si se utiliza un muestreo estratificado proporcional, la muestra debería consistir en estratos que mantengan las mismas proporciones que la población. Si se quiere crear una muestra de 1.000 individuos, las muestras deberán tener los siguientes tamaños:
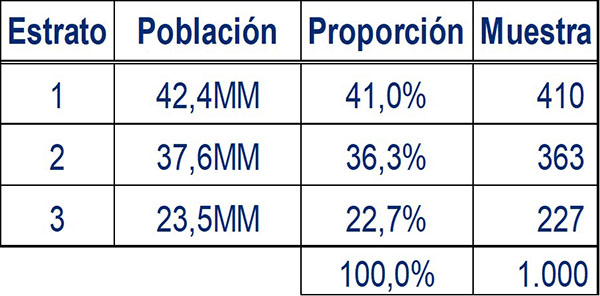
Es muy parecido a reunir una población más pequeña, determinada por las proporciones relativas de los estratos dentro de la población.
En este tipo se asigna el mismo tamaño de muestra a todos los estratos definidos, independientemente del peso de esos estratos dentro de la población.
Un muestreo estratificado uniforme tomando el ejemplo anterior produciría la siguiente muestra para cada estrato:
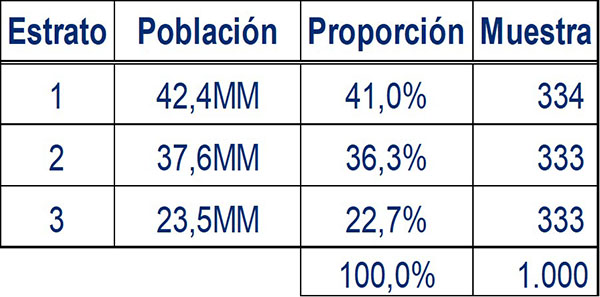
Este método favorece a los estratos que tengan menos peso en la población, al otorgarles el mismo nivel de importancia que los estratos más relevantes.
Esto reduce la efectividad global de la muestra, pero permite estudiar con mayor precisión las características individuales de cada estrato.
En el ejemplo, si se quiere hacer una afirmación específica sobre la población del estrato 3 (mayores de 44), se podrían reducir los errores de muestreo utilizando una muestra de 333 unidades, en lugar de una muestra de 227 unidades, como se obtuvo del muestreo estratificado proporcional.
El muestreo estratificado funciona bien para poblaciones que tengan una variedad de atributos, pero por lo demás no será efectivo si no se pueden formar subgrupos.
Recoge características claves
La principal ventaja del muestreo estratificado es que recoge en la muestra las características claves de la población.
De manera similar a un promedio ponderado, este método de muestreo produce características en la muestra que son proporcionales a la población total.
Mayor precisión estadística
La estratificación da un menor error en la estimación que el método de muestreo simple. Cuanto mayor sea la diferencia entre los estratos, mayor será la ganancia en precisión.
Se tiene una mayor precisión estadística al compararlo con el muestreo simple. Esto es debido a que dentro de los subgrupos es menor la variabilidad, si se compara con las variaciones que se presentan con la población total.
Tamaño de muestra más pequeño
Como esta técnica tiene una exactitud estadística alta, también significa que requiere un tamaño de muestra más pequeño, que puede ahorrar mucho esfuerzo, dinero y tiempo de los investigadores.
Lamentablemente, este método de investigación no se puede utilizar en todos los estudios. La desventaja del método es que se deben cumplir varias condiciones para que sea utilizado correctamente.
Dificultad para encontrar estratos
La desventaja principal es que puede ser difícil identificar estratos apropiados para un estudio. Además, encontrar un listado exhaustivo y definitivo de toda una población puede ser todo un reto.
Complejidad para organizar
Una segunda desventaja es que es más complejo organizar y analizar los resultados en comparación con el muestreo simple.
Los investigadores deben identificar a cada miembro de una población en estudio y clasificarlo en solo una subpoblación. Como resultado, el muestreo estratificado es desventajoso cuando los investigadores no pueden clasificar con confianza a cada miembro de la población en un subgrupo.
La yuxtaposición puede ser un problema si hay sujetos que se dividan en múltiples subgrupos. Cuando se realiza un muestreo simple, tendrán más probabilidad de ser elegidos aquellos que están en múltiples subgrupos. El resultado podría ser una tergiversación o un reflejo inexacto de la población.
Ejemplos como estudiantes universitarios, graduados, hombres y mujeres, lo hacen fácil, ya que son grupos claramente definidos.
Sin embargo, en otras situaciones podría ser mucho más difícil. Se puede imaginar incorporar características tales como raza, origen étnico o religión. El proceso de clasificación se haría más difícil, convirtiendo el muestreo estratificado en un método ineficaz.
Supongamos que un equipo de investigación quiere determinar el promedio de notas de los estudiantes universitarios en Estados Unidos.
El equipo de investigación tiene obvias dificultades para recopilar estos datos de los 21 millones de estudiantes universitarios. Por tanto, decide tomar una muestra de la población, utilizando solo 4.000 estudiantes.
El equipo observa los diferentes atributos de los participantes de la muestra y se pregunta si existe alguna diferencia entre el promedio de notas y la especialización de los estudiantes.
Se encuentra en la muestra que 560 estudiantes son estudiantes de inglés, 1.135 de ciencias, 800 de informática, 1.090 de ingeniería y 415 de matemáticas.
El equipo quiere usar un muestreo estratificado proporcional, donde los estratos de la muestra sean proporcionales a la muestra de la población.
Para ello, el equipo investiga la estadística de los estudiantes universitarios en EE.UU. y encuentra el porcentaje oficial de estudiantes que se especializa: 12% en inglés, 28% en ciencias, 24% en informática, 21% en ingeniería y 15% en matemáticas.
Por tanto, se crean cinco estratos a partir del proceso de muestreo estratificado. El equipo debe confirmar que el estrato de la población sea proporcional al estrato de la muestra. Sin embargo, encuentra que las proporciones no son iguales.
Por consiguiente, el equipo necesita volver a tomar una muestra de la población de 4.000 estudiantes, pero esta vez seleccionando aleatoriamente 480 (12%) estudiantes de inglés, 1.120 (28%) de ciencias, 960 (24%) de informática, 840 (21%) de ingeniería y 600 (15%) de matemáticas.
Con esto, se tiene una muestra estratificada proporcional de estudiantes universitarios, que brinda una mejor representación de estudiantes universitarios en EE.UU.
Los investigadores podrán resaltar un estrato específico, observar los diversos estudios de los estudiantes universitarios de EE.UU. y observar los distintos promedios de notas.
- Adam Hayes (2019). Stratified Random Sampling. Tomado de: investopedia.com.
- Wikipedia, the free encyclopedia (2019). Stratified sampling. Tomado de: en.wikipedia.org.
- Explorable (2019). Stratified Sampling Method. Tomado de: explorable.com.
- Survey Gizmo (2019). What is Stratified Sampling & When is it Used? Tomado de: surveygizmo.com.
- Ashley Crossman (2019). Understanding Stratified Samples and How to Make Them. Thought Co. Tomado de: thoughtco.com.
- Carlos Ochoa (2017). Random sampling: stratified sampling. Tomado de: netquest.com.
