Población estadística: concepto, tipos, ejemplos
La población estadística es el colectivo o conjunto completo de elementos con características en común y que se quiere estudiar. Estos elementos pueden ser personas, seres vivos, objetos inanimados, eventos, actitudes hacia algún suceso y negocios diversos.
Ejemplos de poblaciones son los habitantes de un país entero o de una ciudad, los artículos producidos por una fábrica al cabo de un día o el número de estrellas en la Vía Láctea. Asimismo se puede catalogar como una población estadística a todas las calificaciones obtenidas por los alumnos de una universidad al final del período escolar.
El investigador es quien decide cuáles son las características de interés de la población que va a estudiar. Por ello, siendo tan amplio el abanico de posibilidades, se clasifica a las poblaciones mediante alguna característica sobresaliente, como puede ser su tamaño.
Esto determina la forma más común de clasificar a las poblaciones estadísticas, de modo que las poblaciones, en general, se dice que son infinitas o finitas. Sin embargo, también hay otros atributos distintivos, siempre desde el punto de vista de la investigación a realizar.
Tales atributos se definen previamente para asegurarse de que satisfacen los requerimientos del estudio, y que a la vez ayuden al investigador a dar a la población el tratamiento apropiado.
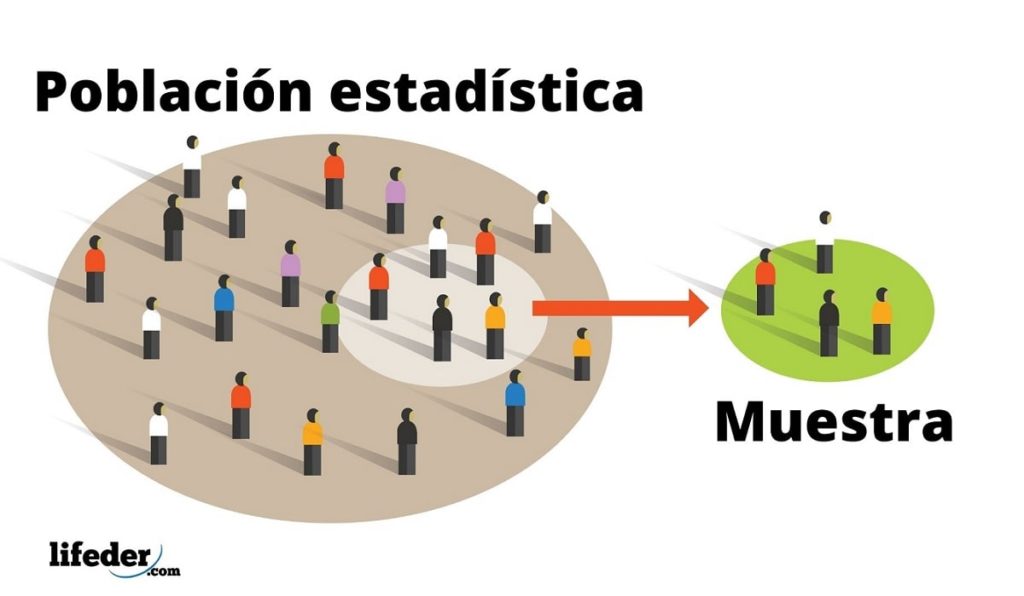
A las poblaciones por lo general se las estudia a través de una muestra cuidadosamente seleccionada: esta es un subconjunto representativo, cuyo menor tamaño le hace más fácil de manejar. Por extensión, las características de la muestra corresponden a las de población dentro un estrecho margen, que el investigador establece a conveniencia usando técnicas estadísticas.
Tipos de poblaciones estadísticas
En principio, puede haber tantos tipos de poblaciones estadísticas como características se quieran incluir en su definición, pero hay algunos criterios que la mayoría de los investigadores usa para clasificarlas y que son universalmente aplicables.
También es preciso destacar que algunas poblaciones encajan sin problema con más de una categoría de las que se mencionan a continuación:
Poblaciones infinitas
Son poblaciones teóricas, ya que contienen una cantidad infinita de elementos. Sin embargo, algunas poblaciones tienen tantos elementos, que en la práctica se consideran infinitas porque el total es muy difícil de determinar.
Ejemplos
-El conjunto de los números reales.
-Número de átomos de oxígeno en el aire de una habitación.
Poblaciones finitas

Tienen un número limitado de componentes, y su número puede ser bastante grande o por el contrario, pequeño.
Ejemplo
-La cantidad de empleados de una compañía.
-Número total de estudiantes de un país.
Poblaciones reales
Se refiere a un grupo de elementos cuya existencia es material o también a las observaciones concretas acerca de algún evento.
Ejemplos
-El total de ballenas azules que existen.
-La actitud de los consumidores hacia un nuevo producto en el mercado.
Poblaciones hipotéticas
En esta categoría se encuentran observaciones acerca de sucesos potenciales y también características psicológicas.
Ejemplo
-Los niveles de ansiedad de un grupo de personas ante la posibilidad de una catástrofe.
Poblaciones estables
Se trata de poblaciones cuyas características se mantienen en el tiempo y el espacio, o bien no varían de manera significativa.
Ejemplo
-El período de rotación de los planetas.
Poblaciones inestables
Por su parte, las poblaciones inestables poseen una o más características variables, tanto en tiempo como en espacio.
Ejemplo

-El conjunto de personas en una ciudad que consume una determinada marca de gaseosa es un ejemplo de población inestable, ya que las preferencias pueden cambiar en un corto plazo, si aparece otro producto con características más llamativas (una marca de la competencia que esté en oferta o que se presente con un nuevo color o sabor…).
Poblaciones dependientes
Están ligadas a una o más características y por ello pueden variar cuando estas cambian, ya sea de modo total o parcial.
Ejemplo
-Las ventas de los productos con poblaciones que dependen, entre otros factores, de la inversión que se haga en publicidad.
Poblaciones binomiales
En esta población se busca determinar la presencia o la ausencia de determinada característica.
Ejemplo
-En estudios sobre la química del agua mineral para el consumo humano, es frecuente señalar la presencia de algún compuesto, como cloruro de sodio o carbonato de calcio.
Poblaciones polinomiales
En las poblaciones polinomiales se pretende llevar a cabo la medida de un conjunto de características.
Ejemplo

-Edad, altura y peso de los estudiantes de una escuela básica.
Poblaciones aleatorias
En estas poblaciones hay cambios debidos al azar o a circunstancias que escapan del control humano.
Ejemplo
-Hay procesos industriales en los cuales variaciones imprevistas afectan a la calidad de los productos finales. Si durante una semana de tormentas eléctricas hubo fallos en el suministro de electricidad, los cuales afectaron una fábrica de vasos de cartón, posiblemente la producción de esa semana no sea de la misma calidad que la producción regular.
Ejemplos de población estadística
A continuación hay una lista de poblaciones ilustrativa de los distintos tipos que se pueden presentar en numerosas áreas. Es importante recalcar nuevamente que una misma población puede pertenecer a más de uno de los tipos descritos, porque tiene características en común con ellas.
– La población total de gatos de un país (población real e infinita).

– Moléculas de agua en el océano Atlántico (es una población real e infinita, ya que contiene una cantidad tal de elementos, que en la práctica es imposible totalizarlos).
– Todos los virus presentes en la Tierra (población real e infinita).
– Número de nacimientos prematuros durante el próximo trimestre (población hipotética, ya que los nacimientos aún no se produjeron, y también es finita).
– Cantidad de animales afectados en la próxima temporada de sequía por posibles incendios forestales (población hipotética y finita).
– Cantidad de estrellas que hay en el núcleo de la Vía Láctea (población finita y estable, puesto que el número de estrellas permanece constante durante largo tiempo y además es real).
-El conjunto de todos los números primos (población infinita, estable y real).
– Niveles de colesterol en la población de países de la Unión Europea (población finita, dependiente, real, inestable).
– Número de supervivientes en caso de una erupción del Vesubio (población hipotética, finita, inestable).
Referencias
- Glosario de Conceptos de Estadística. Recuperado de: psi.uba.ar.
- Statistics by Jim. Populations, Parameters, and Samples in Inferential Statistics. Recuperado de: statisticsbyjim.com.
