Campo eléctrico: qué es, fómula, unidades, intensidad, ejemplos

¿Qué es el campo eléctrico?

El campo eléctrico es la propiedad que tienen los objetos cargados de influir en el espacio que los rodea, la cual es percibida por otros cuerpos cargados eléctricamente. Pero, a diferencia de la fuerza eléctrica entre cargas, el campo eléctrico depende solo de la carga que lo produce.

Michael Faraday (1791-1867), físico inglés, creó el concepto de campo al observar que una carga eléctrica cualquiera influye en el espacio que la rodea, de forma tal que no necesita estar en contacto con otra carga para que se produzca la interacción.

Ni siquiera es necesario que las cargas se encuentren en un medio material, ya que la interacción se puede dar en el vacío.

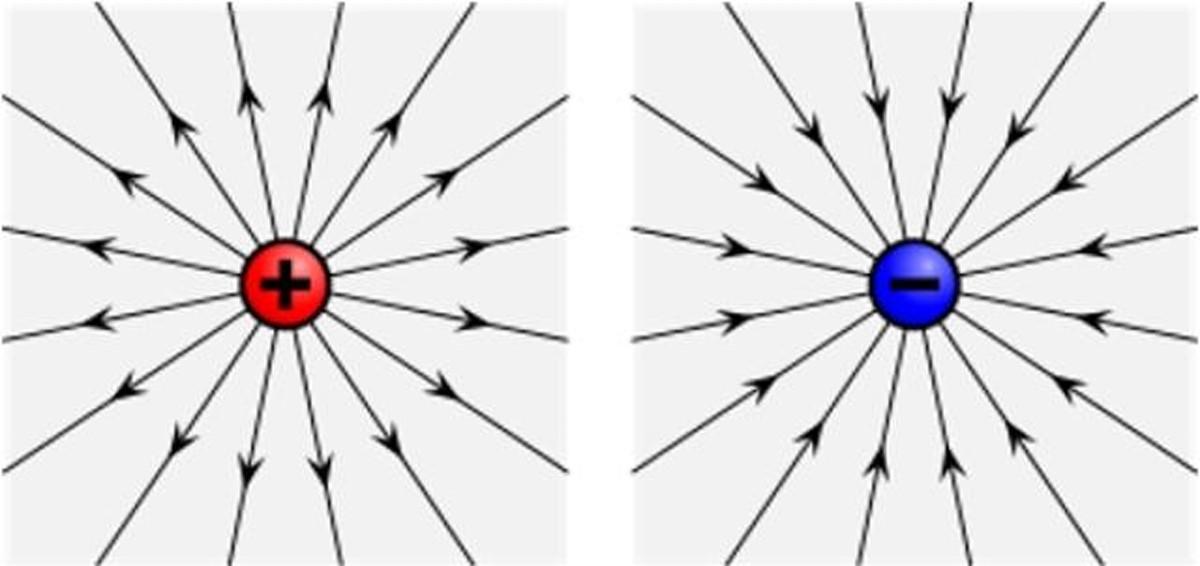
Para visualizar la forma de un campo eléctrico, supóngase una carga puntual y positiva, llamada +q, cuyo tamaño es tan pequeño que no es necesario tomar en cuenta sus dimensiones. El campo que ella produce es capaz de afectar a otras cargas, como, por ejemplo, otra carga puntual positiva de prueba q_o.

La carga de prueba se coloca en distintas ubicaciones alrededor de +q, y por ser ambas positivas, la fuerza que +q ejerce sobre q_o es de repulsión.

Dibujando el vector fuerza sobre la carga q_o en cada punto del espacio que ocupa, y retirándola, queda un conjunto de líneas que emergen radialmente de la carga +q (ver la imagen arriba, a la izquierda).

Al repetir la experiencia con una carga negativa – q, las líneas también son radiales, pero entrantes a – q. En ambos casos, las líneas son tangentes al vector campo eléctrico de la carga, salientes de ella cuando es positiva, y entrantes si es negativa.

Fórmula y unidades

Si en una región del espacio existe un campo eléctrico E, una carga eléctrica q_o experimenta, gracias a él, una fuerza dada por:

F = q_oE

De manera que:

La unidad del campo eléctrico en el Sistema Internacional de unidades SI es newton/coulomb, que se abrevia N/C. También es frecuente expresar el campo eléctrico en términos de una magnitud escalar llamada potencial eléctrico, en cuyo caso la unidad para el campo es el voltio/metro (V/m).

El campo eléctrico de una carga puntual

El campo E es producido por algún objeto con carga q. Haciendo muy pequeña la carga de prueba, es decir, haciendo q_o tender a 0, el vector E es:

La intención al tomar el límite es hacer la carga de prueba lo bastante pequeña como para que su campo no altere el que se quiere calcular.

Si q es una carga puntual, de acuerdo a la ley de Coulomb, la fuerza entre las cargas q y q_o, ambas separadas una distancia r, viene dada por:

Sustituyendo esta expresión en la definición de campo, se obtiene:

Y como se dijo al comienzo, la dirección del campo es radial y el sentido es saliente a la carga cuando esta es positiva, y entrante cuando es negativa.

Intensidad del campo eléctrico

El campo eléctrico es vectorial, y su intensidad hace referencia a su módulo o magnitud, la cual se denota sin negrita. Para una carga puntual, la intensidad de su campo eléctrico es simplemente:

Por ejemplo, la intensidad del campo eléctrico producido por una carga q = − 4.3 μC (μC se lee “microcoulomb” y equivale a la millonésima parte de un coulomb), a una distancia de 2 cm de la carga, es:

Nótese que la distancia de 2 cm se convirtió a metros, multiplicando por la potencia 10⁻², ya que la constante electrostática está en unidades SI. Y aunque la carga es negativa, la intensidad del campo que produce siempre es positiva, pero el vector campo eléctrico es entrante a la carga, como se explicó previamente.

Ejemplos de campo eléctrico

1. Campo eléctrico de una distribución discreta de cargas

A un conjunto de cargas puntuales se le denomina distribución de cargas discretas. En ese caso, el campo eléctrico resultante en el punto P se calcula aplicando el principio de superposición, que es la suma vectorial del campo que cada una de las cargas produce en P:

E_neto = E₁ + E₂ + E₃ + …

La siguiente imagen muestra una distribución compuesta por cinco cargas puntuales y el campo eléctrico que cada una produce en el punto P:

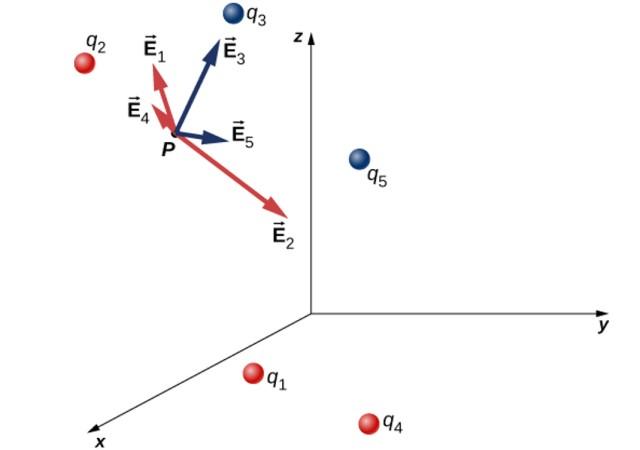
• Las cargas q₃ y q₅ son negativas y el campo que producen es entrante a ellas. Se distinguen en color azul.
• Por su parte, las cargas q₁, q₂ y q₄ son positivas, creando un campo saliente en color rojo.

2. Campo eléctrico de una distribución continua de cargas

Una distribución continua de carga consiste en un objeto extendido, cargado eléctricamente, como el que se muestra en la siguiente figura. Dado que el objeto tiene dimensiones apreciables, el campo que una parte del cuerpo produce en P es sensiblemente distinto al que produce otra más alejada (o más cercana) de P.

Supóngase que se toma una pequeña carga eléctrica de dicho objeto, llamada dq y supuesta positiva, la cual produce en P una pequeña contribución al campo eléctrico total. Dicha contribución es un diferencial del vector campo eléctrico dE.

Como la carga dq es muy pequeña, su campo es como el de una carga puntual, así que puede aplicarse la ecuación antes vista:

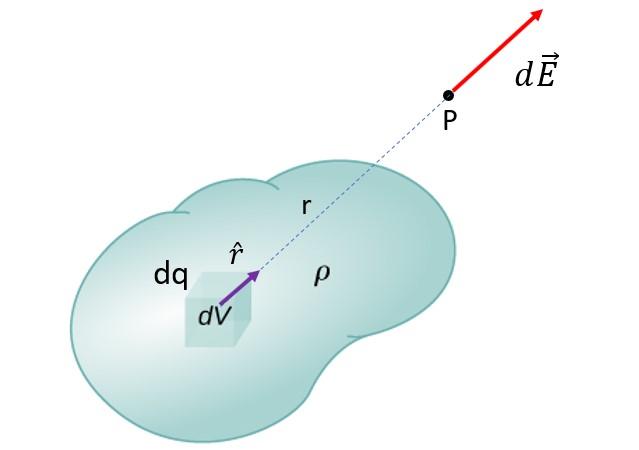
Para obtener el campo total del objeto en el punto P, se suman las contribuciones de todas las dq que se pueden tomar sobre el objeto. Esto conduce a la integral:

Ejercicio resuelto

Una carga puntual Q = 2.0 × 10⁻⁸ C se coloca en un punto P dentro de un campo eléctrico, en el cual experimenta una fuerza ascendente de magnitud 4.0 × 10⁻⁶ N. Calcular:

a) El campo eléctrico en P

b) La fuerza sobre una carga q = −1.0 × 10⁻⁸ C ubicada en P.

Solución a

Sea E la magnitud del campo eléctrico en el cual se coloca a la carga Q. En virtud de este campo, dicha carga experimenta la fuerza ascendente de magnitud F, de modo que:

F = Q∙E

Entonces:

E = F /Q = 4.0×10^–6 N/ 2.0×10^–8 C = 200 N/C.

Siendo positiva la carga, la fuerza y el campo tienen la misma dirección y sentido.

Solución b

La magnitud de la fuerza que actúa sobre q es:

Al ser negativa esta carga, fuerza y campo tienen la misma dirección, pero sentidos contrarios.

Referencias

1. Bauer, W. 2011. Física para Ingeniería y Ciencias. Volumen 2. Mc Graw Hill. 
2. Campo y potencial eléctrico de una carga puntual. Recuperado de: sc.ehu.es.
3. Resnick, R. (1999). Física. Vol. 1. 3a ed. en español. Compañía Editorial Continental S.A. de C.V.
4. Sears, Z. (2016). University Physics with Modern Physics. 14th. Ed. Volume 1. Pearson.
5. University Physics. Electric Field. Vol. 2. Recuperado de: openstax.org.