Fracciones equivalentes a 3/4 (ejemplos y ejercicios resueltos)

Las fracciones equivalentes a 3/4 son aquellas en las que, al dividir el numerador entre el denominador, da como resultado el número decimal 0.75.

Siempre es posible expresar una fracción como un número decimal equivalente, efectuando el cociente del numerador entre el denominador. Si el resultado de esta operación es igual a 0.75, la fracción es equivalente a 3/4, por ejemplo, la fracción 6/8:

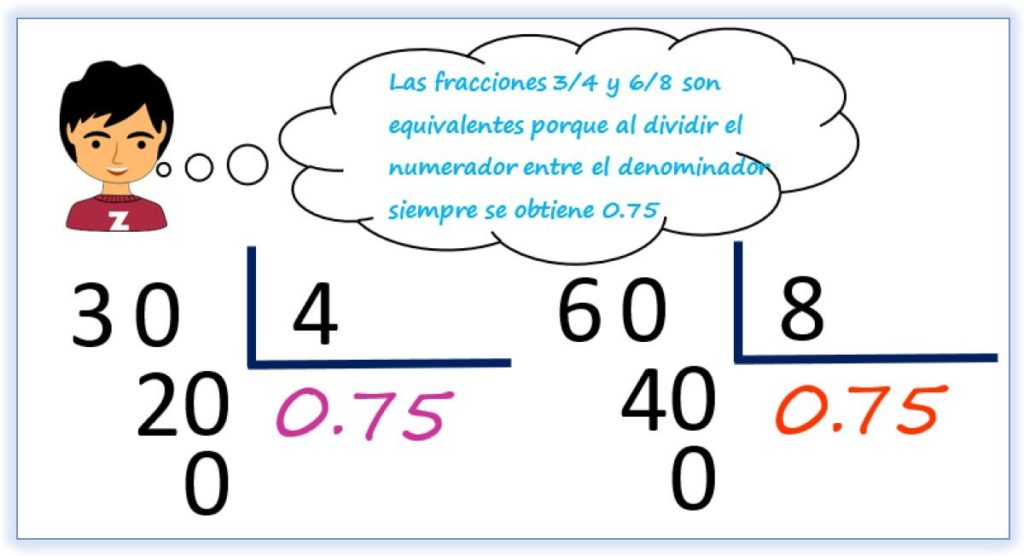
Ahora bien, la fracción 6/8 se obtuvo multiplicando por 2 tanto el numerador como el denominador de ¾. Al multiplicar simultáneamente el numerador y el denominador por una misma cantidad, el valor decimal de una fracción dada no se altera, pero permite obtener fracciones que sean equivalentes a una dada.

Otra manera de encontrar una fracción equivalente a otra sería dividiendo numerador y denominador por una misma cantidad. Sin embargo, en el caso de ¾, no es posible hallar un número tal que divida a la vez al 3 y al 4 y el resultado sea entero. Ello se debe a que 3 y 4 son primos entre sí, por lo no poseen divisores comunes.

Cuando el numerador y el denominador de una fracción son números primos entre sí, se dice que la fracción es irreducible. Por lo tanto, ¾ es irreducible.

Formas de hallar una fracción equivalente a otra

Hay dos maneras muy sencillas de encontrar una fracción equivalente a otra fracción dada: la primera es por reducción y la segunda mediante amplificación.

Reducción y amplificación de fracciones

Reducción

Este procedimiento consiste en hallar un número que sea divisor tanto del numerador como del denominador. Una vez hallado, se procede a dividir tanto numerador como denominador por dicho valor y de inmediato se obtiene una fracción equivalente a la original. Se comprueba que es así haciendo el cociente numerador entre denominador y comparando.

Cuando se desea hallar la fracción irreducible de otra, se divide numerador y denominador de dicha fracción entre el máximo común divisor (MCD) de ambos. La fracción así obtenida es irreducible.

La fracción ¾ es irreducible, como se dijo antes, por ser 3 y 4 primos entre sí, pero el siguiente método permite hallar infinitas fracciones equivalentes a ¾.

Amplificación

Para amplificar una fracción dada, se debe multiplicar el numerador y el denominador por una misma cantidad, no importa si es un número positivo o negativo. Por ejemplo, la fracción 6/8 se obtuvo amplificando ¾ por el factor 2:

Aunque las fracciones tienen diferente numerador y denominador, ambas son iguales.

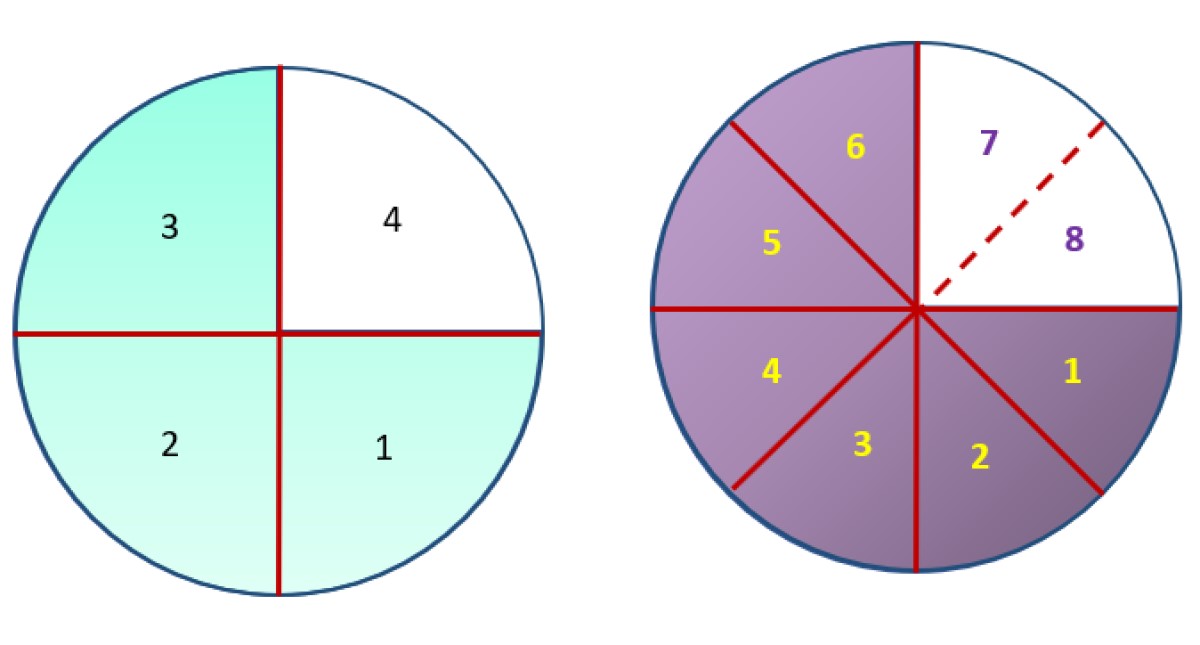
Obsérvese la figura siguiente, que contiene dos círculos idénticos, divididos en partes iguales, aunque de distinto tamaño. Observando cuidadosamente, las áreas en color verde y morado tienen la misma medida, pero el área verde se ha subdivido en 3 partes, de las 4 en total que conforman el círculo de la izquierda. En cambio, el círculo a la derecha se subdividió en 8 partes iguales y el área morada equivale a 6 de ellas.

De esta forma, se puede comprobar gráficamente que ¾ es equivalente a 6/8, puesto que ambas fracciones representan la misma cantidad.

En general, si se multiplica la fracción ¾ por el número n, se obtienen tantas fracciones equivalentes a ella como se quiera:

Es importante destacar que n nunca puede ser igual a 0, ya que la división por 0 no está definida. Ninguna fracción puede tener 0 en su denominador.

¿Cómo saber si una fracción es equivalente a 3/4?

Tal como se explicó al comienzo, una manera de saber si una fracción equivale a ¾ es efectuando el cociente entre el numerador y el denominador. Si resulta 0.75, la fracción es equivalente a ¾, pero hay un par de métodos más para saberlo, que no requieren hacer la división directamente:

Método 1

Supóngase la fracción a/b, y se quiere saber si es equivalente a ¾, es decir, si se cumple que:

Para que sean equivalentes, el producto 4a debe ser igual al producto 3b:

4a= 3b

Método 2

Si la fracción a/b es equivalente a ¾, dividiendo a y b por su máximo común divisor MCD, el resultado debe ser ¾.

Para aclarar el uso de estos métodos, véanse los siguientes ejemplos.

Ejemplos

Ejemplo 1

Determinar si la fracción 150/200 es equivalente a ¾:

Por el método 1

En este caso a = 150 y b = 200, se debe cumplir que:

4a= 3b

• 4 × 150 = 600
• 3 × 200 = 600

Se concluye que 150 / 200 es equivalente a ¾.

Por el método 2

El máximo común divisor de 150 y 300 los divide a ambos exactamente. Se halla descomponiendo ambas cantidades en sus factores primos y luego se multiplican los factores comunes con su menor exponente:

• 150 = 2 × 5² × 3
• 200 = 2³ × 5²

El 2 y el 5 son comunes, se multiplican escogiendo la menor potencia con la que aparecen:

MCD (150, 200) = 2 × 5² = 2 × 25 = 50

Ahora se procede a dividir:

Ejercicios resueltos

Ejercicio 1

Escribir por amplificación cinco fracciones equivalentes a ¾, multiplicando numerador y denominador cada vez por los siguientes números enteros:

a) 3, b) 5, c) (-2), d) 10 y e) 20

Solución a

Solución b

Solución c

Solución d

Solución e

Ejercicio 2

Verificar si las siguientes fracciones son equivalentes a ¾:

a) 18/24; b) 21/28; c) 24/32; d) 27/38;  e) 33/44

Solución a

Empleando el método 1 descrito más arriba:

4a= 3b

Para la fracción 18/24 se tiene que a = 18 y b = 24, entonces:

• 4 × 18= 72
• 3 × 24 = 72

Por lo tanto, 18/24 y 3/4 son equivalentes.

Solución b

Según el método 2, hay que hallar el máximo común divisor (MCD) de 21 y 28, luego dividir ambos entre el resultado, y si se obtiene la fracción 3/4, es que son equivalentes:

21 = 3×7
28 = 4×7 = 2²×7

El factor común es 7, por lo tanto MCD (21,28) = 7, entonces:

Solución c

Para este ejercicio, se comprueba si el cociente entre 24 y 32 es o no 0.75:

24 ÷ 32 = 0.75

Luego, 24/32 es equivalente a 3/4.

Solución d

En la fracción 27/38 se observa que 38 no es múltiplo de 4, por lo tanto, no es equivalente a 3/4. De todas maneras se lleva a cabo el cociente entre 27 y 38:

27 ÷ 38 = 0.710526

De lo cual se concluye que 27/38 no es equivalente a 3/4.

Solución e

Es fácil ver que la fracción 33/44 se obtiene multiplicando el numerador y denominador de 3/4 por 11, así: