Ecuación de Arrhenius: explicación, aplicaciones, ejercicios
¿Qué es la ecuación de Arrhenius?
La ecuación de Arrhenius es una aproximación que relaciona la constante de velocidad de una reacción química en función de la temperatura. Fue establecida en el año 1899 por el químico sueco Svante Arrhenius (1859-1927). Representa una de las contribuciones más fundamentales en el desarrollo de la cinética química.
Esta ecuación debe sus bases teóricas a numerosos científicos, entre ellos Wihelmy (1850), Berthelot (1862) y J. J. Hood (1885). Pero se atribuye la mayor influencia en la creación de la ecuación de Arrhenius a los trabajos realizados por Van’t Hoof (1884), quien estableció una dependencia de las constantes de equilibrio de las reacciones químicas con la temperatura.
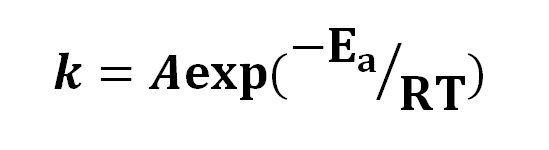
Basándose en la ecuación de Arrhenius, se ha difundido la idea de que un incremento de 10 ºC provoca una duplicación de la velocidad de reacción. Otras interpretaciones que devienen de ella es que las moléculas necesitan de cierta energía de activación para poder reaccionar entre sí.
Asimismo, se señala que la ecuación de Arrhenius es otra forma de desintegración exponencial en la cual decae el valor de la constante de velocidad en función del exponente -Ea/RT, donde Ea es la energía de activación.
Ecuación y explicación
La ecuación de Arrhenius tiene las siguientes dos expresiones:
K = Ae-Ea/RT
Forma de la ecuación usada en química y que está relacionada con los moles de reactivo.
K = Ae-Ea/kBT
Forma de la ecuación usada en física y que está relacionada con las moléculas más, que con los moles.
Ambas derivan de la ecuación de Van’t Hoof para la variación de la constante de equilibrio K en función de la temperatura. La ecuación base es:
d(ln k)/dT = Ea/RT2
La cual se integra asumiendo que Ea es independiente de la temperatura. Entonces tenemos:
ln k = – Ea/RT + ln A
Donde ln A es la constante de integración. Al aplicarse la función exponencial a ambos lados de la ecuación, obtenemos la ecuación de Arrhenius ya introducida.
Componentes
k
Es la constante de velocidad de una reacción química. Su valor puede obtenerse, además del uso de la ecuación de Arrhenius, por la aplicación de la Ley de Velocidad. Representa el número de colisiones entre partículas que produce una reacción por segundo.
A
Es el llamado factor pre-exponencial, el cual representa la frecuencia de las colisiones entre las moléculas de los reactivos con una orientación geométrica apropiada que puede o no producir una reacción química. Si la variación de la temperatura es de poca magnitud, A se suele tomar como constante. Este factor tiene su propia fórmula:
A = Z ρ
Donde Z se conoce como factor de frecuencia o colisión, y ρ el factor geométrico o estérico que señala la orientación relativa de las moléculas en el punto de colisión. La constante A tiene las mismas unidades que la constante de velocidad. En el caso que no exista la energía de activación, la magnitud de A será igual a la de k.
Ea
Es la energía de activación, la cual representa la energía umbral antes de alcanzar el estado de transición: un estado donde las moléculas tienen una forma intermedia entre las moléculas de los reactivos y las moléculas de los productos.
La energía de activación tiene como unidad el kJ/mol. Pero en los cálculos se utiliza como unidad el J/mol. El signo menos (-) que antecede a la Ea, sirve para indicar que su aumento produce una disminución de la velocidad de la reacción, así como su disminución produce un incremento en la velocidad de reacción.
RT
Representa la energía cinética promedio. Mientras, R es la constante universal de los gases, siendo uno de sus valores más usados 8.31 J·K-1·mol-1. Y T es la temperatura absoluta expresada en Kelvin (K).
e
Es la base de los logaritmos naturales o neperianos, teniendo un valor de 2.71828.
e-Ea/RT
Es la fracción de moléculas reaccionantes con energía igual o en exceso con relación a la energía de activación.
Aplicaciones
La mayor parte de las aplicaciones de la ecuación de Arrhenius provienen de su uso en la determinación la constante de velocidad; y por extensión, la velocidad de la reacción, así como su energía de activación.
Por ejemplo, se ha elaborado un modelo químico basado en la ecuación de Arrhenius, que puede predecir las propiedades de los materiales a medida que cambian su temperatura, siendo aplicado en los campos de la geología, la construcción, la ingeniería de los materiales, y en la ciencia de los alimentos.
Se ha aplicado, aunque con ciertas críticas, la ecuación de Arrhenius en la cinética de las reacciones del estado sólido. También se ha utilizado para caracterizar las respuestas de las plantas al estrés hídrico.
La ecuación de Arrenhius sirvió de base para la creación de un modelo matemático, el cual cuantifica el efecto de la temperatura sobre la vida útil de las celdas o baterías de hidruro metálico de níquel.
Asimismo, basándose en la ecuación de Arrhenius se estableció la tasa de descomposición de los desechos porcinos, y del aceite de cocina, bajo diversos contenidos de humedad.
Ejercicios resueltos
Ejercicio 1
¿Cuál es la energía de activación de una reacción si se encuentra que su constante de velocidad se triplica cuando la temperatura sube de 600 K a 610 K?
Partiendo de la ecuación de Arrhenius:
k = A·e-Ea/RT
Despejamos el factor A:
A = k1 / (e-Ea/RT1)
Pero como tenemos dos temperaturas, T1 y T2, habrá dos constantes de velocidad: k1 y k2. El factor A no cambia, por lo que podemos igualarla para la segunda temperatura:
k1 / (e-Ea/RT1) = k2 / (e-Ea/RT2)
Y despejando Ea tendremos:
Ea = R (ln k2/k1) / (1/T1 – 1/T2)
Como k2 es tres veces más grande que k1,
k2 / k1 = 3
ln (3) = 1.099
Y por otro lado:
1 / T1 = 1 / 600 K = 1.66 x 10-3 K-1
1 / T2 = 1 / 610 K = 1.64 x 10-3 K-1
Sustituyendo entonces:
Ea = (8.31 J·K-1·mol-1) (1.099) / (1.66 x 10-3 K-1 – 1.64 x 10-3 K-1)
= 456.5 kJ·mol-1
Ejercicio 2
En una reacción en fase gaseosa la energía de activación es igual a 103 kJ/mol, y la constante de velocidad es de 0.085 min-1. Calcule la constante de velocidad a 323 K.
De la expresión anterior despejamos ln k2/k1:
ln k2/k1 = (Ea/R) (1 /T1 – 1/T2)
Desarrollando la parte derecha de la ecuación:
ln k2/k1 = (103.000 J·mol-1 / 8.31 J·K-1·mol-1)(1/273 K – 1/323 K)
ln k2/k1 = 6.99
Tomando antilogaritmos:
k2/k1 = 1.086
k2 = (k1) (1.086)
= (0.085 min-1) (1.086)
= 0.092 min-1
Referencias
- Whitten, Davis, Peck & Stanley. (2008). Química. (8va ed.). CENGAGE Learning.
- Walter J. Moore. (1963). Physical Chemistry. In Chemical kinetics. Fourth edition, Longmans.
- Ira N. Levine. (2009). Principios de fisicoquímica. Sexta edición. Mc Graw Hill.
- Wikipedia. (2020). Arrhenius Equation. Recuperado de: en.wikipedia.org
- Guenevieve Del Mundo et al. (10 de septiembre de 2020). Arrhenius Equation. Recuperado de: chem.libretexts.org
- Clark Jim. (2013). Rate constants and the Arrhenius equation. Recuperado de: chemguide.co.uk
- The Editors of Encyclopaedia Britannica. (2020). Arrhenius equation. Recuperado de: britannica.com
- Helmenstine, Anne Marie, Ph.D. (28 de agosto de 2020). The Arrhenius Equation Formula and Example. Recuperado de: thoughtco.com
