Suma de polinomios, como se hace, ejemplos, ejercicios
La suma de polinomios es la operación que consiste en adicionar dos o más polinomios, dando como resultado otro polinomio. Para llevarla a cabo es preciso sumar los términos del mismo orden de cada uno de los polinomios e indicar la suma resultante.
Primero repasemos brevemente el significado de “términos del mismo orden”. Un polinomio cualquiera se compone de sumas y/o restas de términos.

Los términos pueden ser productos de números reales y una o más variables, representadas con letras, por ejemplo: 3x2 y -√5.a2bc3 son términos.
Pues bien, los términos del mismo orden son aquellos que tienen el mismo exponente o potencia, aunque pueden tener distinto coeficiente.
-Términos de igual orden son: 5x3, √2 x3 y -1/2x3
-Términos de ordenes diferentes: -2x-2, 2xy-1 y √6x2y
Es importante tener presente que solamente los términos del mismo orden se pueden sumar o restar, operación que se conoce como reducción. En caso contrario la suma simplemente se deja indicada.
Una vez aclarado el concepto de términos del mismo orden, los polinomios se suman siguiendo estos pasos:
–Ordenar primero los polinomios a sumar, todos de la misma manera, ya sea de forma creciente o decreciente, es decir, con las potencias de menor a mayor o viceversa.
–Completar, en caso de que falte alguna potencia en la secuencia.
–Reducir los términos semejantes.
–Indicar la suma resultante.
Índice del artículo
Comenzaremos sumando dos polinomios con una sola variable llamada x, por ejemplo los polinomios P(x) y Q(x) dados por:
P (x) = 2x2 – 5x4 + 2x –x5 – 3x3 +12
Q(x) = x5– 25 x + x2
Siguiendo los pasos descritos, se comienza por ordenarlos en forma decreciente, que es la manera más usual:
P (x) = –x5– 5x4 – 3x3 + 2x2 + 2x +12
Q(x) = x5+ x2 – 25x
El polinomio Q(x) no está completo, se ve que faltan potencias con exponente 4, 3 y 0. Esta última es simplemente el término independiente, el que no tiene letra.
Q(x) = x5+ 0x4 + 0x3 + x2 – 25x + 0
Una vez realizado este paso, ya están listos para sumar. Se pueden ir sumando los términos semejantes y luego indicar la suma, o bien colocar los polinomios ordenados uno debajo del otro y reducir por columnas, de esta forma:
– x5 – 5x4 – 3x3 + 2x2 + 2x +12
+ x5 + 0x4 + 0x3 + x2 – 25x + 0 +
———————————————————-
0x5–5x4 – 3x3 +3x2 – 23x + 12 = P (x) + Q (x)
Es importante notar que cuando se suma, se hace de forma algebraica respetando la regla de los signos, de esta manera 2x + (-25 x) = -23x. Es decir, si los coeficientes tienen distinto signo se restan y el resultado lleva el signo del mayor.
Cuando se trata de polinomios con más de una variable, se elige una de ellas para ordenarlo. Por ejemplo, supongamos que se pide sumar:
R (x,y) = 5x2 – 4y2 + 8xy – 6y3
Y:
T (x,y) = ½ x2– 6y2 – 11xy + x3y
Se escoge una de las variables, por ejemplo la x para ordenar:
R (x,y) = 5x2 + 8xy – 6y3 – 4y2
T (x,y) = + x3y + ½ x2 – 11xy – 6y2
De inmediato se completan los términos faltantes, de acuerdo a los que cada polinomio tiene:
R (x,y) = 0x3y + 5x2 + 8xy – 6y3 – 4y2
T (x,y) = + x3y + ½ x2 – 11xy + 0y3 – 6y2
Y ya ambos están listos para reducir los términos semejantes:
0x3y + 5x2 + 8xy – 6y3 – 4y2
+ x3y + ½ x2 – 11xy + 0y3 – 6y2 +
—————————————————————–
+ x3y + 11/2x2 – 3xy – 6y3 – 10y2 = R(x,y) + T(x,y)
En la siguiente suma de polinomios, indicar el término que debe ir en el espacio en blanco para obtener el polinomio suma:
-5x4 + 0x3 + 2x2 + 1
x5 + 2x4 – 21x2 + 8x – 3
2x5 +9x3 -14x
————————————————
-6x5+10x4 -0x3 + 5x2 – 11x + 21
Solución
Para obtener -6x5 se requiere un término de la forma ax5, tal que:
a + 1+ 2 = -6
Por lo tanto:
a = -6-1-2 = -9
Y el término buscado es:
-9x5
-Se procede de manera similar para encontrar el resto de los términos. Aquí está el de exponente 4:
-5 + 2 + a = 10 → a = 10+5-2 = 13
El término faltante es: 13x4.
-Para las potencias de x3 es inmediato que el término debe ser -9x3, de esta manera el coeficiente del término cúbico es 0.
-En cuanto a las potencias al cuadrado: a + 8 – 14 = -11 → a = -11 – 8 + 14 = -5 y el término es -5x2.
-El término lineal se obtiene mediante a +8 -14 = -11 → a = -11 + 14 – 8 = -5, siendo el término faltante -5x.
-Por último el término independiente es: 1 -3 + a = -21 → a = -19.
Un terreno plano está cercado como se muestra en la figura. Hallar una expresión para:
a) El perímetro y
b) Su área, en términos de las longitudes señaladas:
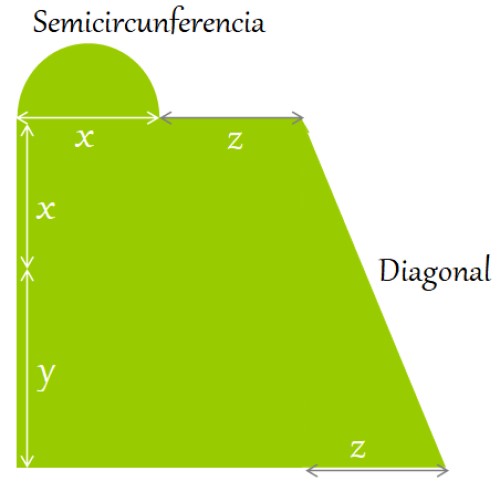
Solución a
El perímetro se define como la suma de los lados y contornos de la figura. Comenzando en la esquina inferior izquierda, en el sentido de las manecillas del reloj, se tiene:
Perímetro = y + x + longitud de la semicircunferencia + z + longitud de la diagonal + z + z + x
La semicircunferencia tiene diámetro igual a x. Como el radio es la mitad del diámetro, se tiene que:
Radio= x/2.
La fórmula para la longitud de una circunferencia completa es:
L = 2π x Radio
Entonces:
Longitud de la semicircunferencia = ½. 2π (x/2) =πx/2
Por su parte la diagonal se calcula con el teorema de Pitágoras aplicado a los lados: (x+y) que es lado vertical y z, que es el horizontal:
Diagonal = [(x+y)2 + z2]1/2
Se sustituyen estas expresiones en la del perímetro, para obtener:
Perímetro = y + x + πx/2 + z + [(x+y)2 + z2]1/2+ z + x + z
Se reducen los términos semejantes, ya que la suma requiere que el resultado se simplifique al máximo:
Perímetro = y + [x + π (x/2) + x] + z + z + z + [(x+y)2 + z2]1/2 = y + (2 + π /2)x + 3z
Solución b
El área resultante es la suma del área del rectángulo, el semicírculo y el triángulo rectángulo. Las fórmulas para dichas áreas son:
–Rectángulo: base x altura
–Semicírculo: ½ π (Radio)2
–Triángulo: base x altura /2
Área del rectángulo
(x+y). (x+z) = x2 + xz +yx + yz
Área del semicírculo
½ π (x/2)2 = π x2 / 8
Área del triángulo
½ z(x+y) = ½ zx + ½ zy
Área total
Para encontrar el área total se suman las expresiones encontradas para cada área parcial:
Área total = x2 + xz +yx + yz + (π x2 / 8) + ½ zx + ½ zy
Y finalmente se reducen todos los términos que sean semejantes:
Área total = (1 + π/8) x2 + 3/2 xy + 3/2yz + yx
- Baldor, A. 1991. Álgebra. Editorial Cultural Venezolana S.A.
- Jiménez, R. 2008. Álgebra. Prentice Hall.
- Math is Fun. Adding and subtracting polynomials. Recuperado de: mathsisfun.com.
- Monterey Institute. Sumando y restando polinomios. Recuperado de: montereyinstitute.org.
- UC Berkeley. Algebra of polynomials. Recuperado de: math.berkeley.edu.
