Propiedades de los limites (con ejemplos)

Las propiedades de los límites son el conjunto de reglas y procedimientos algebraicos utilizados para determinarlos. El concepto de límite es fundamental para el cálculo y hallar su valor no tiene por qué ser una tarea complicada, siempre que sus propiedades se manejen con soltura.

A continuación se presenta una lista de las más importantes, acompañadas de ejemplos de  aplicación.

Sean b, c, n, A y B números reales, y f y g funciones tales que verifican lo siguiente:

Entonces se tienen las siguientes propiedades:

1. Límite por sustitución directa

En primera instancia, el límite de una función f cuando x → c se puede calcular sustituyendo directamente x=c en la función. Si la función existe en x=c, entonces el límite es:

Ejemplo

Hallar el límite de f(x) = x² cuando x → 4

Solución

El límite resuelve simplemente sustituyendo x = 4 en f(x) = x², ya que no existe inconveniente en efectuar la operación:

Si el límite de una función f(x) cuando x → c existe y vale L, dicho límite es único.

Por lo tanto, los límites laterales, que son aquellos cuando x → c^– (se lee “x tiende a c desde la izquierda”) y cuando x → c⁺ (se lee “x tiende a c por la derecha”), existen ambos y tienen el mismo valor L, aun si la función no está definida en x = c.

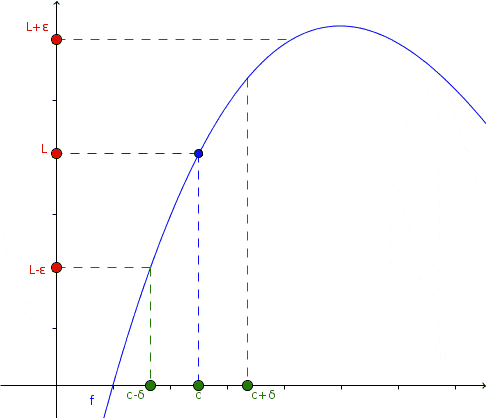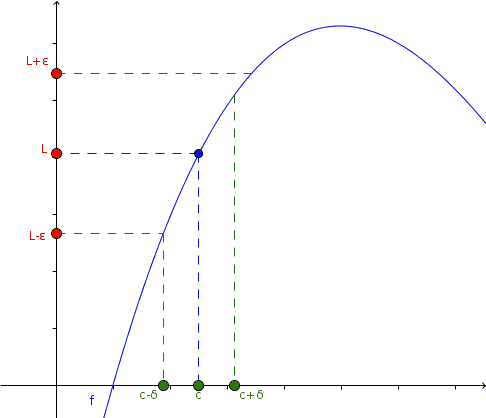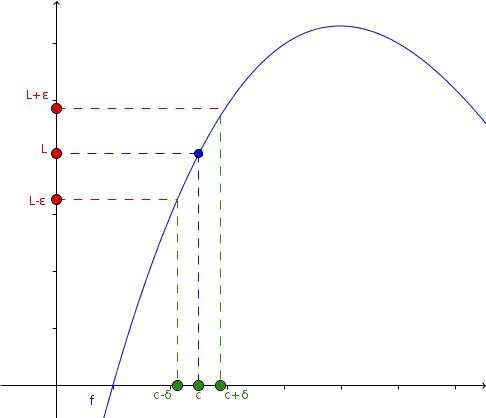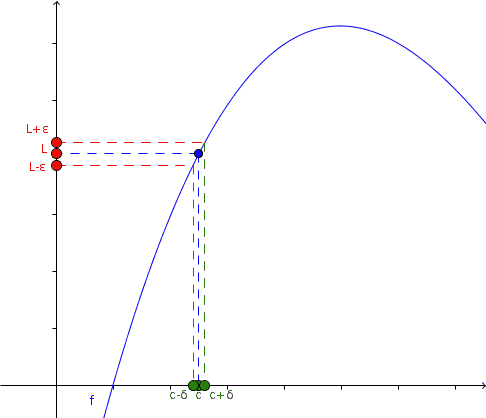
En la animación se observa este acercamiento y lo que sucede con la función en ese caso: tanto si se acerca por la izquierda como por la derecha a x =c, el valor de la función a su vez se acerca a L.

Matemáticamente se expresa de esta forma:

Ejemplo

Calcular el límite de f(x) cuando x → 1 si es que existe, donde f(x) está dada por:

1// 4x-x^{2}, /: si/: x/geq 1/end{matrix}/right. ." src="https://latex.codecogs.com/gif.latex?f(x)=%5Cleft%5C%7B%5Cbegin%7Bmatrix%7D&space;4-x,%5C:&space;si%5C:&space;x1%5C%5C&space;4x-x%5E%7B2%7D,&space;%5C:&space;si%5C:&space;x%5Cgeq&space;1%5Cend%7Bmatrix%7D%5Cright.&space;." class="">

Solución

Esta es una función por partes o definida a trozos, que consiste en la recta 4 -x para los valores de x 1 y en la parábola 4 – x² cuando x es igual a 1 o mayor que 1.

Podemos acercarnos a x =1 desde la izquierda, en tal caso se toma la parte de la función que es válida para x1:

Como los límites laterales son iguales, se deduce que el límite de la función cuando x → 1 existe y vale 3.

3. Límite de una constante

El límite de una constante es el valor de dicha constante, sin importar el valor al cual tiende la variable:

Ejemplo

Calcular:

4. Límite de la función identidad

Si f(x) = x, se cumple siempre que:

Ejemplo

Calcular:

5. Límite del producto de una constante por una función

En este caso, la constante sale fuera del límite y pasa a multiplicarlo, así:

Calcular, si existe, el siguiente límite:

La constante 5 queda fuera multiplicando al límite y se aplica la propiedad de sustitución:

6. Límite de la suma

El límite de la suma de dos funciones f y g es la suma de los límites:

Ejemplo 

Encontrar el siguiente límite si existe:

Se aplica primero la propiedad de la suma de los límites y después la de sustitución directa, ya que las operaciones no presentan dificultad:

 7. Límite de la resta

En el caso del límite de la resta de dos funciones, se procede de manera análoga que para la suma: el límite de la resta es la resta de los límites:

Ejemplo

Calcular el siguiente límite:

Se aplica la propiedad del límite de la resta de dos funciones y después la de sustitución directa, puesto que todas las operaciones se pueden realizar sin problema:

8. Límite del producto

El límite del producto de dos funciones f y g es el producto de los límites:

Calcular este límite:

Solución

9. Límite del cociente

El límite del cociente de dos funciones f y g es el cociente de los límites, siempre que el límite de g(x) cuando x → c sea diferente de 0, ya que la división por 0 no está definida. Entonces:

Ejemplo

Calcular, si existe, el valor del siguiente límite:

En primera instancia se aplica la propiedad del límite del cociente, para obtener el cociente de los límites:

Ahora se aplica la propiedad de sustitución para encontrar cada límite:

Y dado que B ≠0, el límite buscado es el cociente A/B:

10. Límite de una potencia

El límite de una potencia de exponente n, equivale al límite elevado a la dicha potencia, de la siguiente manera:

Si se tiene, por ejemplo, el límite de una potencia de x, resulta:

De acuerdo a la propiedad 4, este límite es:

Caso 2: límite de una raíz

Una raíz n-ésima se puede escribir en forma de exponente fraccionario, de allí que:

Importante: si el índice de la raíz es par, es necesario que el límite de f(x) cuando x → c sea mayor o igual a 0, ya que no existen raíces reales pares de cantidades negativas.

Ejemplos

Determinar, aplicando las propiedades anteriores, los siguientes límites si es que existen:

Solución a

Mediante la propiedad del límite de una potencia y de la sustitución directa se obtiene:

Solución b

11. Límite de una exponencial

Para encontrar el límite de una exponencial de base b y exponente f(x), hay que elevar la base al límite de la función f(x) del siguiente modo:

Ejemplo

Hallar si es que existe, el siguiente límite:

En este límite la base es el número e y la función f(x) = x², por lo tanto hay que calcular primero el límite de x²  cuando x tiende a 1:

Luego se aplica la propiedad del límite de la exponencial:

12. Límite de la función potencial exponencial

El límite cuando x → c de una función f(x), que a su vez está elevada a otra función g(x) se expresa mediante:

Ejemplo

Calcular el siguiente límite, si existe:

Solución

Para aplicar la propiedad anterior, primeramente se identifican f(x) = x–1 y g(x) = 2x y luego se calculan los límites respectivos:

1. Ayres, F. 2000. Cálculo. 5ed. Mc Graw Hill.
2. Leithold, L. 1992. Cálculo con Geometría Analítica. HARLA, S.A.
3. Mathematics Libre Texts. Limits. Recuperado de: math.liibretexts.org.
4. Matemovil. Leyes y propiedades de los límites. Recuperado de: matemovil.com.
5. Larson, R. 2010. Cálculo de una variable. 9na. Edición. McGraw Hill.
6. Purcell, E. J., Varberg, D., & Rigdon, S. E. (2007). Cálculo. México: Pearson Educación.
7. Universo Fórmulas. Propiedades de los límites. Recuperado de: universoformulas.com