Elipse: elementos, tipos, ejemplos, ejercicios resueltos

¿Qué es una elipse?

Una elipse es un conjunto de puntos de coordenadas (x, y), para los cuales la suma de las distancias a dos puntos fijos, llamados focos, es constante. A su vez los focos están separados entre sí una distancia igual a 2c.

Las elipses se encuentran en la naturaleza. Por ejemplo, está en el movimiento de la Tierra alrededor del Sol, ya que como lo demostró el astrónomo alemán Johannes Kepler (1571-1630) hacia 1609, los planetas, satélites y algunos cometas del sistema solar, describen trayectorias elípticas.

Además la forma elíptica se encuentra en el diseño de construcciones arquitectónicas, forma parte de un tratamiento médico para destruir cálculos renales y sirve para dar forma a objetos diversos como tanques y otros recipientes.

En la figura superior se muestra una elipse con sus dos focos, situados equidistantes del centro de la figura y sobre el eje más largo. La condición que debe cumplir un punto P para pertenecer a la elipse es que la suma de las distancias a cada foco sea fija:

d₁ + d₂ = constante.

Por eso, cuando un jardinero quiere trazar una elipse grande sobre el terreno, lo primero que hace es plantar dos estacas en el suelo, donde van los focos. Después toma una cuerda de buen tamaño, amarra sus extremos a las estacas, y apoyando un palo sobre la cuerda lo desliza sobre ella para marcar el surco elíptico sobre la tierra blanda. Este es el método del jardinero para trazar elipses.

Elementos de la elipse

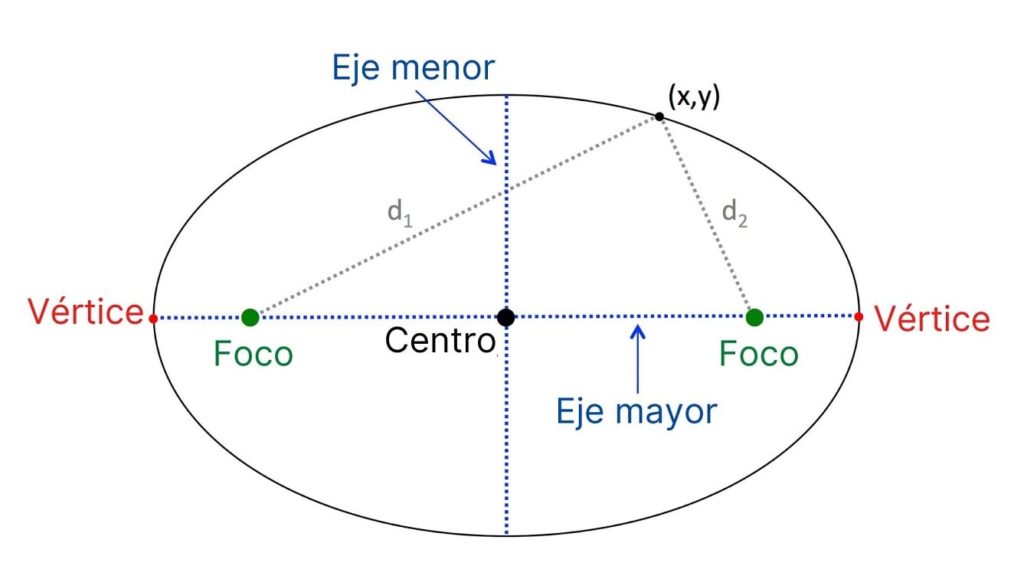
Estos son los elementos principales de la elipse:

1. Focos, puntos fijos ubicados sobre el eje más largo de la elipse.
2. Vértices, son los dos puntos de la elipse por los que pasa la recta que une a los focos.
3. Eje mayor, es la cuerda que une a los vértices y que también contiene a los focos.
4. Centro, punto medio del eje mayor, que en la figura corresponde al punto de coordenadas (h,k). Cada foco se encuentra equidistante del centro y a una distancia c del mismo.
5. Eje menor, es la cuerda que pasa por el centro y es perpendicular al eje mayor.
6. Radios vectores, segmentos que unen a cada foco con un punto P de la elipse.
7. Eje focal, recta sobre la que se encuentran los focos.
8. Distancia focal, es la distancia entre los focos, denotada como 2c.
9. Eje secundario, eje perpendicular al eje mayor, que es a la vez mediatriz del segmento que une a los focos.
10. Centro de simetría, punto coincidente con el centro de la elipse, donde se cruzan los ejes de simetría de la misma.
11. Ejes de simetría, rectas que contienen a los ejes mayor y menor de la elipse.

Tipos de elipse

Hay dos tipos de elipse:

• Las que tienen el eje mayor horizontal.
• Las que tienen el eje mayor vertical.

Seguidamente se las describe matemáticamente:

Elipse con el eje mayor horizontal

Sea el punto C de coordenadas (h,k) el centro de la elipse, la longitud del eje mayor es 2a y la longitud del eje menor igual a 2b, con a > b.

La ecuación de esta elipse es:

Elipse con el eje mayor vertical

Con los mismos parámetros de la elipse con eje mayor horizontal, la elipse con eje mayor vertical se escribe como:

En ambos casos, la distancia del foco al centro c está relacionada con los semiejes mayor y menor mediante:

c² = a² − b²

Ejemplos de elipses

Elipse horizontal

En la siguiente imagen se muestra una elipse cuyo eje mayor es horizontal. El centro está en el punto (0,0) y los focos en (-3,0) y (3,0) respectivamente. El punto P (0,-4) destacado pertenece a la elipse.

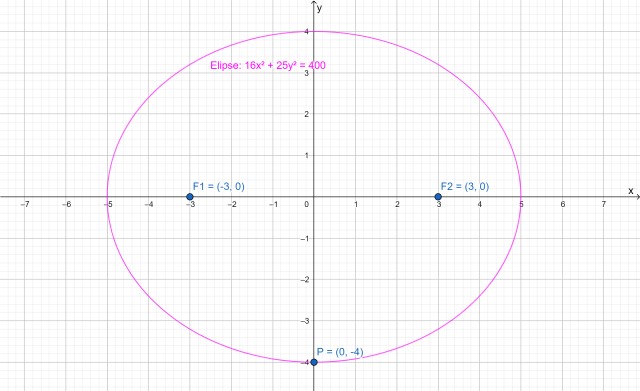
La ecuación de esta elipse es:

16x² + 25y² = 400

No es difícil expresar esta ecuación en la forma canónica, basta con dividir todos los términos entre 400 y simplificar convenientemente (ver el ejercicio resuelto más adelante).

Elipse vertical

La siguiente es una elipse vertical, cuyo eje mayor coincide con el eje y. Está centrada en el punto (0,0) y su ecuación es:

36x² + 9y² = 324

La propiedad de reflexión

Consiste en lo siguiente: si en uno de los focos de la elipse se coloca un reflector o una fuente sonora, las ondas emitidas se reflejan hacia el otro foco. Es una buena forma de redirigir las ondas hacia donde se necesite de su energía.

Es por eso que en los salones elípticos, cuando una persona habla estando en uno de los focos, un oyente ubicado en el otro foco la escucha claramente.

Y en medicina esta propiedad de reflexión se aprovecha para destruir los cálculos renales poniendo al paciente en uno de los focos de una tina elíptica llena de agua, mientras que el generador de ondas de ultrasonido se coloca en el otro foco. Las ondas se reflejan en los cálculos y los fragmentan en partículas de menor tamaño, que se expulsan luego a través de la orina.

El radiotelescopio SKA

Este radiotelescopio es el más grande en su tipo y se espera que comience a funcionar en 2021. Su superficie es de 1 km cuadrado y por eso se le llama SKA (en inglés son las siglas de Square Kilometre Array).

Aprovechando la propiedad de reflexión de las elipses, la estructura consta de un arreglo de 3000 antenas con forma elíptica de unos 15 m de ancho, repartidas entre Australia y Sudáfrica. Con este instrumento, 50 veces más sensible que los que se encuentran en uso ahora misma, se espera echar una mirada al universo cuando este aún era muchísimo más joven: unos mil millones de años apenas.

Ejercicio resuelto

Encontrar las ecuaciones canónicas de las elipses mostradas en las figuras 2 y 3 y en cada caso determinar las longitudes de los semiejes mayor y menor, así como distancias focales.

Solución

Para la elipse horizontal, cuya ecuación es 16x² + 25y² = 400, se dividen todos los términos entre 400, resultando:

El semieje mayor “a” mide 5 y el menor “b” mide 4, que también se advierte observando la imagen cuidadosamente. En cuanto a la distancia focal, se tiene que:

c² = a² − b²

c² = 25 − 16=9 ⇒ c=√9 = 3

Por lo tanto c = 3 es la distancia entre el centro y uno de los focos. Ambos focos distan entre sí una distancia 2c=6.

En cuanto a la elipse vertical 36x² + 9y² = 324 se tiene:

c=√27 ≅ 5.2

Por lo tanto la distancia entre los focos es 10.4 unidades.

Referencias

1. Hoffman, J. Selección de temas de Matemática. Volumen 3.
2. Stewart, J. 2006. Precálculo: Matemáticas para el Cálculo. 5ta. Edición. Cengage Learning.
3. Universo Fórmulas. La elipse. Recuperado de: universoformulas.com.
4. Wikipedia. Square Kilometre Array. Recuperado de: es.wikipedia.org.
5. Zill, D. 1984. Álgebra y Trigonometría. McGraw Hill.