¿Qué es el equilibrio de la partícula? (Con ejemplos)
El equilibrio de la partícula es un estado en que se encuentra una partícula cuando las fuerzas externas que actúan sobre ellas se encuentran anuladas entre sí. Esto supone que mantiene un estado constante, de tal manera que puede darse de dos maneras diferentes en función de la situación concreta.
La primera es estar en equilibrio estático, en el cual la partícula se encuentra inmóvil; y la segunda es el equilibrio dinámico, donde la sumatoria de fuerzas se anula, pero sin embargo la partícula tiene movimiento rectilíneo uniforme.

El modelo de partícula es una aproximación muy útil para estudiar el movimiento de un cuerpo. Consiste en suponer que toda la masa del cuerpo se concentra en un solo punto, sin importar el tamaño del objeto. De esta manera se puede representar un planeta, un automóvil, un electrón o una bola de billar.
Índice del artículo
- 1 La fuerza resultante
- 2 Diagramas de cuerpo libre
- 3 Formas de aplicar la condición de equilibrio
- 4 Rozamientos
- 5 Ejemplo resuelto
- 6 Referencias
Sobre el punto que representa al objeto es donde actúan las fuerzas que lo afectan. Todas estas fuerzas pueden sustituirse por una sola que hace el mismo efecto, la cual se denomina fuerza resultante o fuerza neta y se denota como FR o FN.
De acuerdo a la segunda Ley de Newton, cuando existe una fuerza resultante no equilibrada, el cuerpo experimenta una aceleración proporcional a la fuerza:
FR = m.a
Donde a es la aceleración que adquiere el objeto gracias a la actuación de la fuerza y m es la masa del objeto. ¿Qué sucede si el cuerpo no está acelerado? Precisamente lo que se indicó al comienzo: el cuerpo está en reposo o se mueve con movimiento rectilíneo uniforme, el cual carece de aceleración.
Para una partícula en equilibrio es válido asegurar que:
FR = 0
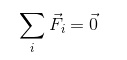
Como sumar vectores no implica forzosamente sumar los módulos, los vectores deben descomponerse. Así, es válido expresar:
Fx = m.ax = 0; Fy = m.ay = 0; Fz = m.az = 0
Con la finalidad de visualizar las fuerzas que actúan sobre la partícula conviene hacer un diagrama de cuerpo libre, en el cual se representan mediante flechas todas las fuerzas que actúan sobre el objeto.
Las ecuaciones anteriores son de naturaleza vectorial. Al descomponer las fuerzas, se las distingue mediante signos. De este modo se hace posible que la suma de sus componentes sea nula.
Las siguientes son indicaciones importantes para que el dibujo resulte de utilidad:
– Escoger un sistema de referencia en el que la mayor cantidad de fuerzas queden ubicadas sobre los ejes de coordenadas.
– El peso siempre se dibuja verticalmente hacia abajo.
– En caso de existor dos o más superficies en contacto existen fuerzas normales, que siempre se dibujan empujando al cuerpo y perpendicularmente a la superficie que la ejerce.
– Para una partícula en equilibrio pueden existir rozamientos paralelos a la superficie de contacto y oponiéndose al posible movimiento, si es que la partícula se considera en reposo, o definitivamente en oposición, si la partícula se mueve con MRU (movimiento rectilíneo uniforme).
– Si hay una cuerda, la tensión se dibuja siempre a lo largo de ella y tirando del cuerpo.
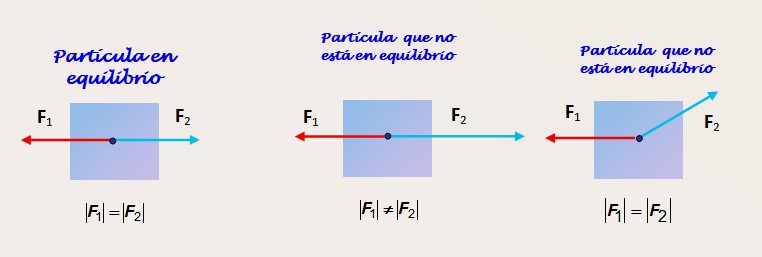
En la figura 2 se muestra una partícula sobre la cual actúan dos fuerzas. En la figura de la izquierda la partícula recibe la acción de dos fuerzas F1 y F2 que tienen la misma magnitud y actúan en la misma dirección y en sentidos opuestos.
La partícula está en equilibrio, pero sin embargo con la información suministrada no es posible saber si el equilibrio es estático o dinámico. Se necesita más información acerca del sistema inercial de referencia desde el cual se observa al objeto.
La figura del centro muestra a la misma partícula, que en esta oportunidad no se encuentra en equilibrio, ya que la magnitud de la fuerza F2 es mayor que la de de F1. Por lo tanto hay una fuerza no equilibrada y el objeto tiene una aceleración en la misma dirección que F2.
Finalmente en la figura de la derecha observamos un cuerpo que tampoco está en equilibrio. A pesar de que F1 y F2 tienen igual magnitud, la fuerza F2 no está en la misma dirección que 1. La componente vertical de F2 no es contrarrestada por ninguna otra y la partícula experimenta una aceleración en esa dirección.
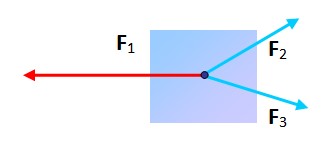
¿Puede una partícula sometida a tres fuerzas estar en equilibrio? Sí, con tal de que al colocar punta y extremo de cada una, la figura resultante sea un triángulo. En tal caso la suma vectorial es nula.
Una fuerza que frecuentemente interviene en el equilibrio de la partícula es el roce estático. Se debe a la interacción del objeto representado por la partícula con la superficie de otro. Por ejemplo un libro en equilibrio estático sobre una mesa inclinada se modela como una partícula y tiene un diagrama de cuerpo libre como el siguiente:
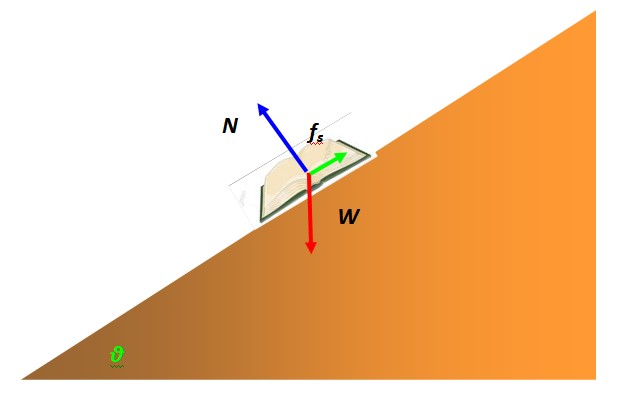
La fuerza que impide que el libro resbale por la superficie del plano inclinado y se mantenga en reposo es el rozamiento estático. Depende de la naturaleza de las superficies en contacto, que microscópicamente presentan rugosidades con picos que se traban unos a otros, dificultando el movimiento.
El valor máximo del rozamiento estático es proporcional a la fuerza normal, la que ejerce la superficie sobre el objeto apoyado, pero perpendicular a dicha superficie. En el ejemplo del libro está indicada en color azul. Matemáticamente se expresa así:
fs más∝ N
La constante de proporcionalidad es el coeficiente de roce estático μs, el cual se determina experimentalmente, es adimensional y depende de la naturaleza de las superficies en contacto.
fs máx = μs N
Si una partícula está en equilibrio dinámico, el movimiento ya tiene lugar y el roce estático no interviene más. En caso de estar presente alguna fuerza de rozamiento que se oponga al movimiento, actúa el roce dinámico, cuya magnitud es constante y está dada por:
fk = μk N
Donde μk es el coeficiente de roce dinámico, que también depende del tipo de superficies en contacto. Al igual que el coeficiente de roce estático, es adimensional y su valor se determina experimentalmente.
El valor del coeficiente de roce dinámico suele ser menor que el de roce estático.
El libro de la figura 3 está en reposo y tiene una masa de 1.30 kg. El plano tiene ángulo de inclinación de 30º. Encuentre el coeficiente de roce estático entre el libro y la superficie del plano.
Es importante seleccionar un sistema de referencia adecuado, véase la siguiente figura:
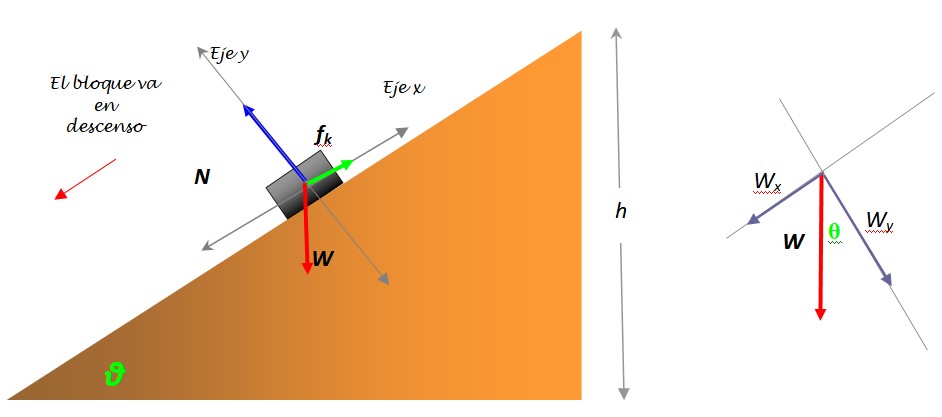
El peso del libro tiene magnitud W = mg, sin embargo es necesario descomponerlo en dos componentes: Wx y Wy, ya que es la única fuerza que no cae justo encima de alguno de los ejes de coordenadas. La descomposición del peso se observa en la figura de la izquierda.
Wy = mg.cosθ = 1.30 x 9.8 x cos 30º N = 11.03 N
Wx = mg.senθ = 1.30 x 9.8 x sen 30º = 6.37 N
La 2da. Ley de Newton para el eje vertical es:
N – Wy = 0
N = mg. cos θ = 11.03 N.
Aplicando la 2da. Ley de Newton para el eje x, eligiendo como positiva la dirección del posible movimiento:
Wx – fs = 0
El roce máximo es fsmáx= μsN, por lo tanto:
Wx – μsN = 0
μs = Wx / N = 6.37/11.03=0.58
- Rex, A. 2011. Fundamentos de Física. Pearson. 76 – 90.
- Serway, R., Jewett, J. (2008). Física para Ciencias e Ingeniería. Volumen 1. 7ma. Ed. Cengage Learning. 120 – 124.
- Serway, R., Vulle, C. 2011. Fundamentos de Física. 9na Ed. Cengage Learning. 99-112.
- Tippens, P. 2011. Física: Conceptos y Aplicaciones. 7ma Edición. MacGraw Hill. 71 – 87.
- Walker, J. 2010. Physics. Addison Wesley. 148-164.
