Equilibrio de traslación: condiciones, ejemplos, ejercicios
Se afirma que un objeto está en equilibrio de traslación cuando la sumatoria de las fuerzas que sobre él actúan es nula. Esto no significa que necesariamente exista el reposo, pero el movimiento, en caso de existir, sería rectilíneo uniforme o bien exclusivamente rotacional, en caso de tratarse de un objeto extenso.
Las condiciones de equilibrio mecánico tienen su fundamento en las leyes de Newton de la Mecánica. En efecto, la primera ley nos dice que un objeto está en reposo o moviéndose con movimiento rectilíneo uniforme MRU, siempre que ninguna fuerza neta actúe sobre él.

Ahora bien, la fuerza neta o fuerza resultante es simplemente la suma vectorial de todas las fuerzas que actúan sobre el objeto. De acuerdo a la segunda ley de Newton, esta suma debe ser igual al producto entre la masa y la aceleración, pero si el objeto no está acelerado, dicha suma se anula.
Y al no existir aceleración están las dos posibilidades mencionadas: el cuerpo está en reposo, es decir, no se traslada, o si lo hace, tiene que ser con MRU. En el primer caso se habla de equilibrio trasnacional estático, y en el segundo, dinámico.
El equilibrio de traslación es un factor importante en muchos aspectos de la ingeniería, por ejemplo en la construcción. Los elementos que componen un edificio: vigas, cables, armazones y más, deben estar en equilibrio para garantizar la estabilidad del recinto.
También se busca el equilibrio de traslación en estructuras móviles, como escaleras mecánicas, bandas de transportación y en la práctica de numerosos deportes.
Índice del artículo
- 1 Condición del equilibrio de traslación
- 2 Ejemplos de equilibrio de traslación
- 3 Ejercicio resuelto
- 4 Referencias
Supongamos que sobre un cuerpo actúan varias fuerzas, a las que denotamos como F1, F2, F3…. Fn, utilizando letra negrita para destacar el hecho de que las fuerzas son vectores y deben sumarse como tales.
A la suma vectorial de todas estas fuerzas se le denomina fuerza resultante o fuerza neta. Si dicha sumatoria tiene como resultado el vector nulo, se cumple la condición para el equilibrio de traslación:
F1+ F2+ F3….+ Fn = 0
Esta condición se puede escribir de manera compacta utilizando la notación de sumatoria:
∑ Fi = 0
En términos de las componentes de la fuerza resultante, la ecuación anterior, que es vectorial, se puede desglosar en tres ecuaciones escalares, una para cada componente de la fuerza resultante:
∑ Fix = 0; ∑ Fy = 0 y ∑ Fz = 0
En la práctica, no es fácil anular la sumatoria de fuerzas, porque el rozamiento es una fuerza de contacto entre superficies que difícilmente se cancela por completo con alguna otra fuerza.
Esta es la razón de que los objetos reales casi nunca estén exentos de las fuerzas externas, y como consecuencia se dificulta obtener el equilibrio de traslación.
Así que los ingenieros utilizan mecanismos para reducir el roce, como los cojinetes y el uso de aceites lubricantes.
El diagrama de cuerpo libre es un esquema en el que se dibujan las fuerzas que actúan sobre el cuerpo. Cuando se busca el equilibrio de traslación, dichas fuerzas deben estar balanceadas. Por ejemplo, si está actuando una fuerza vertical dirigida hacia abajo, como el peso, entonces debe existir una fuerza vertical hacia arriba que tenga exactamente la misma magnitud.
Esta fuerza la puede suministrar la mano que aguanta al objeto para que no caiga, una cuerda o simplemente la superficie de una mesa.
Si hay una fuerza tangencial a la superficie, como el rozamiento cinético o estático, debe haber otra fuerza contraria para que exista el balance. Por ejemplo, observemos la pesa que cuelga de las cuerdas mostradas en la figura siguiente.
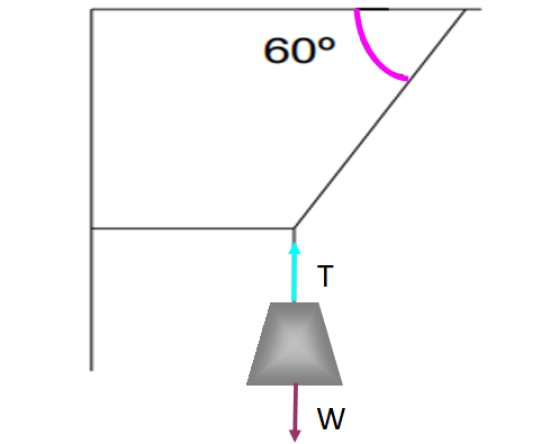
La pesa se mantiene en equilibrio de traslación y sin moverse, gracias a la cuerda vertical que la sujeta ejerciendo una tensión T que compensa al peso W. Cada fuerza se ha representado sobre la pesa mediante una flecha, cada una de igual tamaño y con la misma dirección, pero sentido contrario.
La fuerza equilibrante
Supongamos que sobre un objeto actúa un conjunto de fuerzas. A esto se le denomina un sistema de fuerzas del cual se puede hallar la resultante tal como se explicó anteriormente: sumando vectorialmente cada una de las fuerzas del sistema.
Pues bien, a la fuerza opuesta a esta resultante se la denomina fuerza equilibrante. Si la fuerza resultante es FR y la fuerza equilibrante es E, entonces:
E + FR = 0
Por lo tanto:
E = – FR
Muchos objetos que encontramos cotidianamente, dentro y fuera de casa, están en equilibrio de traslación:
Las edificaciones y las carreteras se construyen para que permanezcan estables y no se vuelquen o colapsen. Sin embargo, en los rascacielos y en general los edificios muy altos, cierta flexibilidad es necesaria para resistir la acción del viento.
Los libros en una biblioteca y los productos en los anaqueles de las tiendas son objetos que permanecen en equilibrio de traslación y sin moverse.
Los muebles, el televisor de pantalla plana y los cuadros en la pared, así como las lámparas que cuelgan del techo, por mencionar algunos objetos, se encuentran en equilibrio de traslación.
Los semáforos se sujetan mediante postes y cables, para que no se caigan. Sin embargo, sabemos que el viento los hace oscilar.
Las luces del alumbrado público también están en equilibrio de traslación, fijas en los postes de luz, como la farola de la imagen principal.
¿Qué magnitud debe tener la fuerza fs de roce estático para que la caja de la figura se mantenga en reposo en medio del plano inclinado un ángulo α de 37º? La masa de la caja es m = 8 kg.
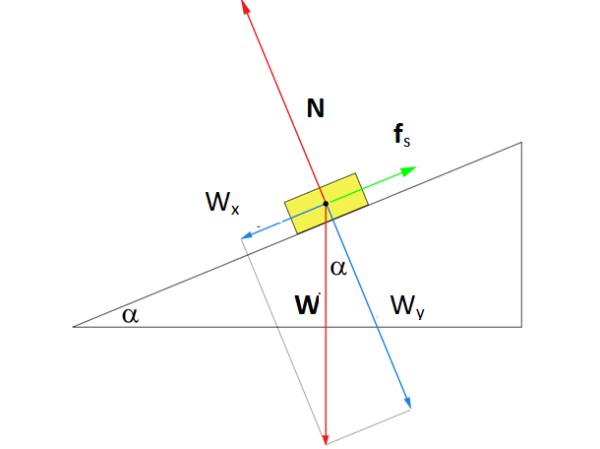
En la figura se muestra el diagrama de cuerpo libre de la caja sobre el plano. Hay tres fuerzas actuando sobre ella: el peso W, dirigido verticalmente hacia abajo, la normal N, que es la fuerza perpendicular que ejerce la superficie del plano sobre la caja, y finalmente la fuerza de roce estático fs que se opone a que la caja resbale cuesta abajo.
La condición de equilibrio de traslación establece que:
W + N + fs = 0
Pero hay que recordar que esta es una suma vectorial y para llevarla a cabo es preciso descomponer las fuerzas en componentes a lo largo de los ejes coordenados.
En la figura se ha dibujado un sistema de coordenadas en el cual el eje x corre paralelo a la superficie del plano inclinado. Con esta elección, el roce estático cae sobre dicho eje, mientras que la normal está sobre el eje y. El peso es la única fuerza que resulta inclinada y hay que descomponer con ayuda de la trigonometría:
Wx = W. sen α
Wy = W. cos α
La sumatoria de fuerzas a lo largo de cada eje es:
∑ Fy = N – Wy = 0
∑ Fx = fs – Wx = 0
De esta última ecuación se deduce que:
fs = Wx
Y como Wx = W. sen α y la magnitud del peso a su vez es W = m.g, siendo g el valor de la gravedad, entonces la magnitud del roce estático es simplemente:
fs = m⋅g⋅sen α = 8 kg × 9.8 m/s2 × sen 37º = 47.2 N.
- Bauer, W. 2011. Física para Ingeniería y Ciencias. Volumen 1. Mc Graw Hill.
- Figueroa, D. (2005). Serie: Física para Ciencias e Ingeniería. Volumen 2. Dinámica. Editado por Douglas Figueroa (USB).
- Giambattista, A. 2010. Physics. 2nd. Ed. McGraw Hill.
- Serway, R., Jewett, J. (2008). Física para Ciencias e Ingeniería. Volumen 1. 7ma. Ed. Cengage Learning.
- Tippens, P. 2011. Física: Conceptos y Aplicaciones. 7ma Edición. McGraw Hill.
