Leyes de Kepler: explicación, ejercicios, experimento
Las leyes de Kepler sobre el movimiento planetario fueron formuladas por el astrónomo alemán Johannes Kepler (1571-1630). Kepler las dedujo basándose en el trabajo de su maestro el astrónomo danés Tycho Brahe (1546-1601).
Brahe recopiló cuidadosamente los datos de los movimientos planetarios a lo largo de más de 20 años, con una precisión y exactitud sorprendentes, si se toma en cuenta que para la época aún no se había inventado el telescopio. La validez de sus datos sigue vigente aún hoy en día.
Índice del artículo
- 1 Las 3 leyes de Kepler
- 2 La ley de gravitación universal y la tercera ley de Kepler
- 3 Ejercicios
- 4 Experimento
- 5 Referencias
Las leyes de Kepler establecen:
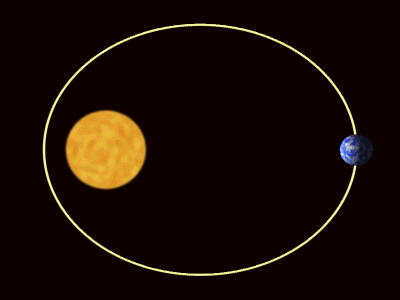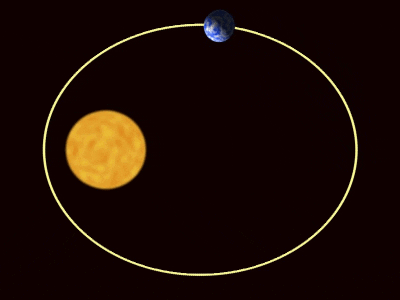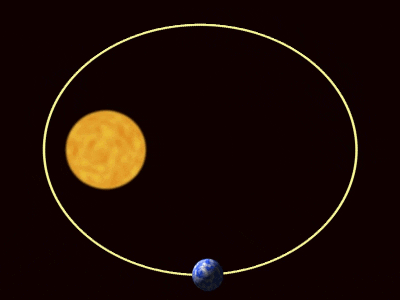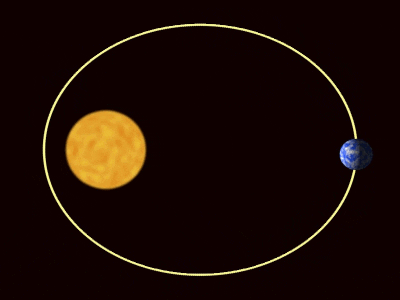
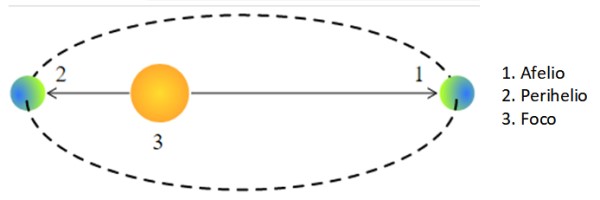
-Primera ley: todos los planetas describen órbitas elípticas con el Sol en uno de los focos.
–Segunda ley o ley de las áreas iguales: una línea dirigida desde Sol hasta cualquier planeta (radio focal), barre áreas iguales en tiempos iguales.
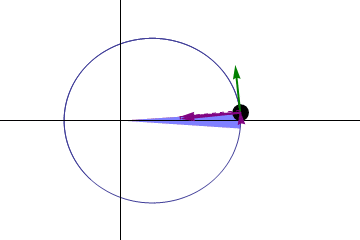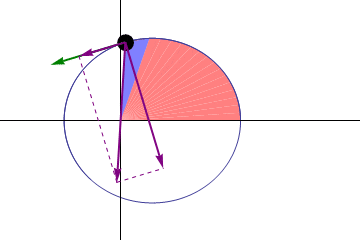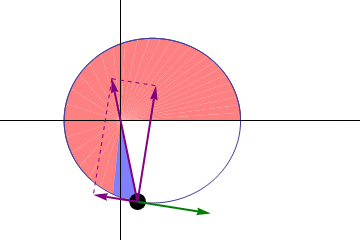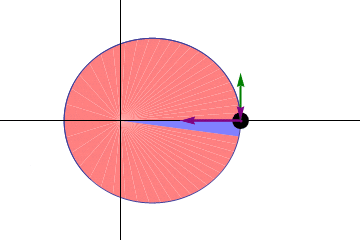
–Tercera ley: el cuadrado del tiempo que le toma a cualquier planeta orbitar alrededor del Sol, es proporcional al cubo de su distancia promedio al Sol.
Sea T dicho tiempo, llamado período orbital, y r la distancia promedio, entonces:
T2 es proporcional a r3
T = k r3
Esto significa que el cociente T2/ r3 es el mismo para todos los planetas, lo cual hace posible calcular el radio orbital, si se conoce el período orbital.
Cuando T se expresa en años y r en unidades astronómicas UA*, la constante de proporcionalidad vale k=1:
T2= r3
*Una unidad astronómica equivale a 150 millones de kilómetros, que es la distancia promedio entre la Tierra y el Sol. El período orbital de la Tierra es de 1 año.
La ley de gravitación universal establece que la magnitud de la fuerza de atracción gravitatoria entre dos objetos de masas M y m respectivamente, cuyos centros están separados una distancia r, viene dada por:
F = G mM /r2
G es la constante de gravitación universal y su valor es G = 6.674 x 10 -11 N.m2/kg2 .
Ahora bien, las órbitas de los planetas son elípticas con una excentricidad muy pequeña.
Esto quiere decir que la órbita no se aleja mucho de una circunferencia, salvo en algunos casos como el planeta enano Plutón. Si aproximamos las órbitas a la forma circular, la aceleración del movimiento del planeta es:
ac = v2/r
Dado que F =ma, tenemos:
G mM /r2 = m.v2/r
Aquí v es la velocidad lineal del planeta alrededor del Sol, supuesto estático y de masa M, mientras que la del planeta es m. Entonces:
Esto explica que los planetas más alejados del Sol tengan una menor velocidad orbital, ya que esta depende de 1/√r.
Como la distancia que viaja el planeta es aproximadamente la longitud de la circunferencia: L = 2πr y se tarda un tiempo igual T, el período orbital, se obtiene:
v = 2πr /T
Igualando ambas expresiones para v se obtiene una expresión válida para T2, el cuadrado del período orbital:
Y esta es precisamente la tercera ley de Kepler, ya que en esta expresión el paréntesis 4π2 /GM es constante, por lo tanto T2 es proporcional a la distancia r elevada al cubo.
La ecuación definitiva para el período orbital se obtiene extrayendo raíz cuadrada:
¿Cuánto vale la masa del Sol? Es posible averiguarlo mediante esta ecuación. Sabemos que el período orbital de la Tierra es de un año y el radio orbital es 1 UA, equivalente a 150 millones de kilómetros, así que tenemos todos los datos necesarios.
En nuestra ecuación anterior, despejamos M, no sin antes convertir todos los valores al Sistema Internacional de Unidades SI:
1 año = 3.16 x 107 segundos.
1 UA = 150 millones de km = 1.5 x1011 m.
Aunque Kepler tenía en mente solo los planetas cuando derivó sus famosas leyes, estas también son válidas para el movimiento de satélites y los demás cuerpos del sistema solar, como veremos seguidamente.
Sabiendo que la órbita de Júpiter es 5.19 veces mayor que la de la Tierra, encuentre el período orbital de Júpiter.
Solución
De acuerdo a la definición de la Unidad Astronómica, Júpiter dista del Sol 5.19 UA, por lo tanto, de acuerdo a la tercera ley de Kepler:
T2= r3= (5,19)3 años
Por lo tanto T = (5,19)3/2 años= 11.8 años
El cometa Halley visita al Sol cada 75.3 años. Encontrar:
a) El semieje mayor de su órbita.
b) La medida del afelio, si el perihelio mide 0.568 UA.
Solución
El cometa Halley visita al Sol cada 75.3 años. Encontrar:
a) El semieje mayor de su órbita.
b) La medida del afelio, si el perihelio mide 0.568 UA.
Solución a
Cuando un planeta o cualquier otro astro se encuentra en su punto más cercano al Sol, se dice que está en el perihelio, y cuando está más alejado, en afelio. En el caso especial de una órbita circular, r en la tercera ley de Kepler es el radio de la órbita.
Sin embargo, en la órbita elíptica el cuerpo celeste se encuentra más o menos alejado del Sol, siendo el semieje mayor “a” el promedio entre el afelio y el perihelio:
Por lo tanto, sustituimos r por a en la tercera ley de Kepler, lo cual resulta para el Halley en:
T2= a3→ a = (T)2/3 → a = (75.3) 2/3 UA= 17.832 UA
Solución b
a = ½ (Perihelio + Afelio)
17.832 = ½ (0.568+ Afelio) → Afelio = 2 x 17.832 – 0.568 UA = 35.10 UA.
Analizar el movimiento de los planetas requiere semanas, meses y hasta años de cuidadosa observación y registro. Pero en el laboratorio se puede llevar a cabo un experimento a escala muy sencillo para probar que la ley de las áreas iguales de Kepler se cumple.
Para ello se requiere un sistema físico en el que la fuerza que rige al movimiento sea central, condición suficiente para que se cumpla la ley de las áreas. Tal sistema consiste en una masa atada a una larga cuerda, con el otro extremo del hilo fijo a un soporte.
Se aparta la masa un pequeño ángulo de su posición de equilibrio y se le imprime un ligero impulso, de modo que ejecute un movimiento ovalado (casi elíptico) en el plano horizontal, como si fuese un planeta en torno al Sol.
Sobre la curva descrita por el péndulo, podemos probar que barre áreas iguales en tiempos iguales, si:
-Consideramos radios vectores que van desde el centro de atracción (punto inicial de equilibrio) hasta la posición de la masa.
-Y barremos entre dos instantes consecutivos de igual duración, en dos distintas zonas del movimiento.
Cuanto más largo el hilo del péndulo y menor el ángulo que se aparta de la vertical, la fuerza restauradora neta será más horizontal y la simulación se asemeja al caso del movimiento con fuerza central en un plano.
Entonces el óvalo descrito se aproxima a una elipse, tal como la que recorren los planetas.
-Hilo inextensible
-1 masa o bolita metálica pintada de blanco que hace las veces de lenteja de péndulo
-Regla graduada
-Transportador
-Cámara fotográfica con disco estroboscópico automático
-Soportes
-Dos fuentes de iluminación
-Una lámina de papel o cartón negro
Se necesita el montaje de la figura para tomar fotos de destellos múltiples del péndulo a medida que sigue su trayectoria. Para ello hay que poner la cámara justo arriba del péndulo y el disco estroboscópico automático enfrente de la lente.
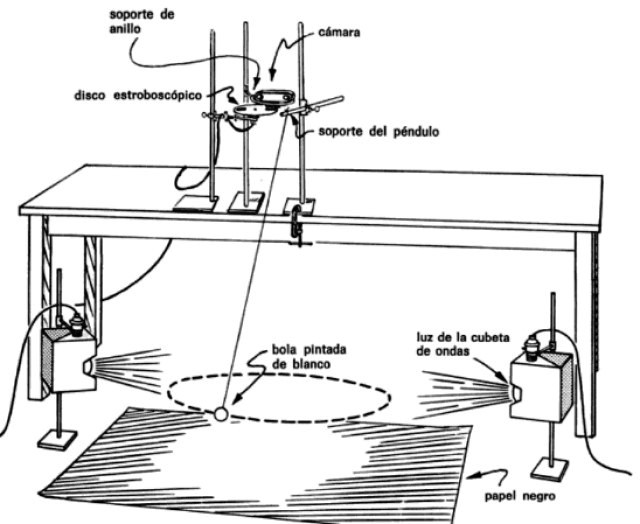
De esta manera se obtienen imágenes a intervalos de tiempo regulares del péndulo, por ejemplo cada 0.1 o cada 0.2 segundos, lo cual permite saber el tiempo que le tomó moverse de un punto al otro.
También hay que iluminar la masa del péndulo convenientemente, poniendo las luces a ambos lados. La lenteja debe pintarse de color blanco para mejorar el contraste sobre el fondo, que consiste en un papel negro extendido sobre el suelo.
Ahora hay que chequear que el péndulo barre áreas iguales en tiempos iguales. Para ello se escoge un intervalo de tiempo y se marcan sobre el papel los puntos ocupados por el péndulo en dicho intervalo.
Sobre la imagen se traza una línea desde el centro del óvalo hasta dichos puntos y así tendremos la primera de las áreas barridas por el péndulo, que es aproximadamente un sector elíptico como el que se muestra a continuación:
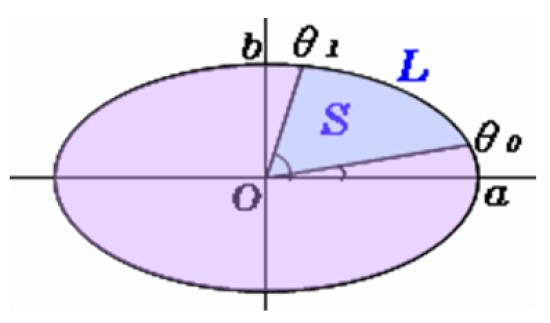
Cálculo del área de la sección elíptica
Con el transportador se miden los ángulos θo y θ1, y se utiliza esta fórmula para hallar S, el área del sector elíptico:
S = F(θ1) – F(θo)
Con F(θ) dado por:
Nótese que a y b son los semiejes mayor y menor respectivamente. El lector solamente debe preocuparse de medir cuidadosamente los semiejes y los ángulos, ya que hay calculadoras online para evaluar esta expresión fácilmente.
Sin embargo, si insiste en hacer el cálculo a mano, hay que recordar que el ángulo θ se mide en grados, pero al momento de ingresar los datos a la calculadora, los valores deben estar expresados en radianes.
Luego hay que marcar otro par de puntos en los cuales el péndulo haya invertido el mismo intervalo de tiempo, y dibujar el área correspondiente, calculando su valor con el mismo procedimiento.
Comprobación de la ley de las áreas iguales
Finalmente resta comprobar que la ley de las áreas se cumple, es decir, que en tiempos iguales se barren áreas iguales.
¿Los resultados se desvían un poco de lo esperado? Hay que tener presente siempre que todas las medidas están acompañadas de su respectivo error experimental.
- Keisan Online Calculator. Area of an elliptical sector calculator. Recuperado de: keisan.casio.com.
- Openstax. Kepler’s Law of Planetary Motion. Recuperado de: openstax.org.
- PSSC. Física de Laboratorio. Editorial Reverté. Recuperado de: books.google.co.
- Palen, S. 2002. Astronomy. Schaum Series. McGraw Hill.
- Pérez R. Sistema sencillo con fuerza central. Recuperado de: francesphysics.blogspot.com
- Stern, D. Las tres leyes de Kepler del movimiento planetario. Recuperado de: phy6.org.
