Ley de Watt: qué es, ejemplos, aplicaciones

La ley de Watt se aplica a circuitos eléctricos y establece que la potencia eléctrica P suministrada por un elemento de circuito, es directamente proporcional al producto entre la tensión de la alimentación V del circuito y la intensidad de corriente I que circula por él.

La potencia eléctrica es un concepto muy importante, porque señala que tan rápido es un elemento para transformar energía eléctrica en alguna otra forma de energía. Matemáticamente, la definición dada de la ley de Watt se expresa así:

P = V.I

En el Sistema Internacional de Unidades (SI), la unidad de potencia recibe el nombre de watt y se abrevia W, en honor a James Watt (1736-1819), ingeniero escocés pionero de la revolución industrial. Dado que la potencia es energía por unidad de tiempo, 1 W equivale a 1 joule/segundo.

Todos estamos familiarizados con el concepto de potencia eléctrica de una u otra manera. Por ejemplo, los dispositivos eléctricos caseros de uso común siempre traen especificada su potencia, incluyendo las bombillas, las hornillas eléctricas o refrigeradores, entre otros.

Índice del artículo

• 1 Ley de Watt y elementos de circuito
  • 1.1 Ley de Watt y ley de Ohm
• 2 Aplicaciones
  • 2.1 Ejemplo 1
  • 2.2 Ejemplo 2
• 3 Referencias

Ley de Watt y elementos de circuito

La ley de Watt se aplica a elementos de circuito con diverso comportamiento. Puede tratarse de una batería, una resistencia u otro. Entre los extremos del elemento se establece una diferencia de potencial V_B – V_A = V_AB y la corriente circula en sentido de A hacia B, como lo indica la siguiente figura:

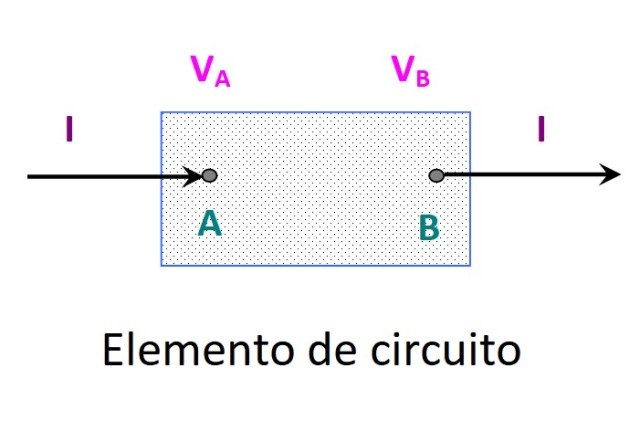
En un tiempo muy pequeño dt, pasa una cierta cantidad de carga dq, de forma que el trabajo realizado sobre ella viene dado por:

dW = V.dq

Donde dq está relacionada con la corriente como:

dq =I.dt

Entonces:

dW = V. I.dt

dW/dt = V. I

Y como la potencia es trabajo por unidad de tiempo:

P = V.I

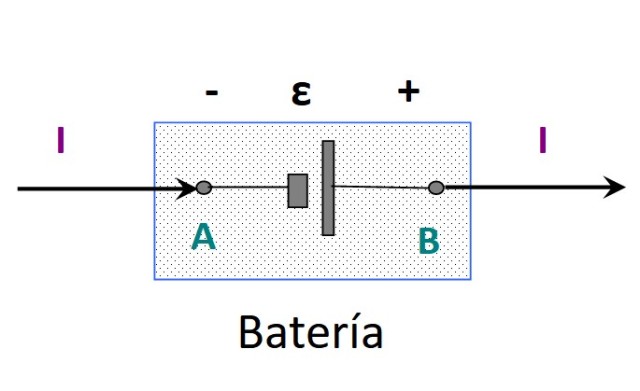
-Si V_AB > 0, las cargas que pasan por el elemento ganan energía potencial. El elemento suministra energía a partir de alguna fuente. Podría ser una batería.

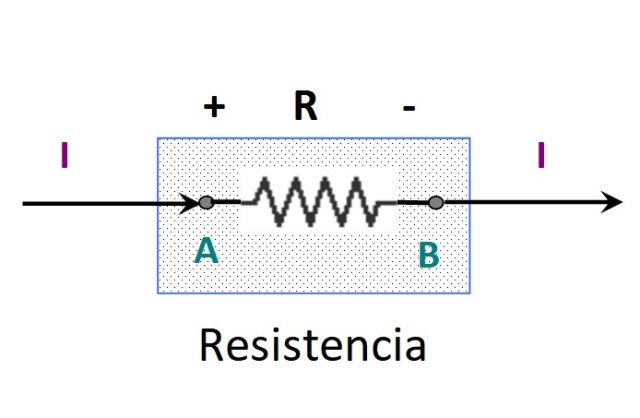
-Si V_AB 0, las cargas pierden energía potencial. El elemento disipa energía, tal como una resistencia.

Nótese que la potencia suministrada por una fuente no depende únicamente del voltaje, sino también de la corriente. Esto es importante para explicar por qué las baterías de los automóviles son tan grandes, tomando en cuenta que apenas suministran 12 V.

Lo que sucede es que el motor de arranque necesita una corriente elevada, durante un breve tiempo, que provea la potencia necesaria para arrancar al automóvil.

Ley de Watt y ley de Ohm

Si el elemento de circuito es una resistencia, se pueden combinar la ley de Watt y la ley de Ohm. Esta última establece que:

V = I. R

Que al sustituir en la ley de Watt conduce a:

P = V. I = (I.R).I = I².R

También pueden obtenerse una versión en función de la tensión y la resistencia:

P = V. (V/R) = V² / R

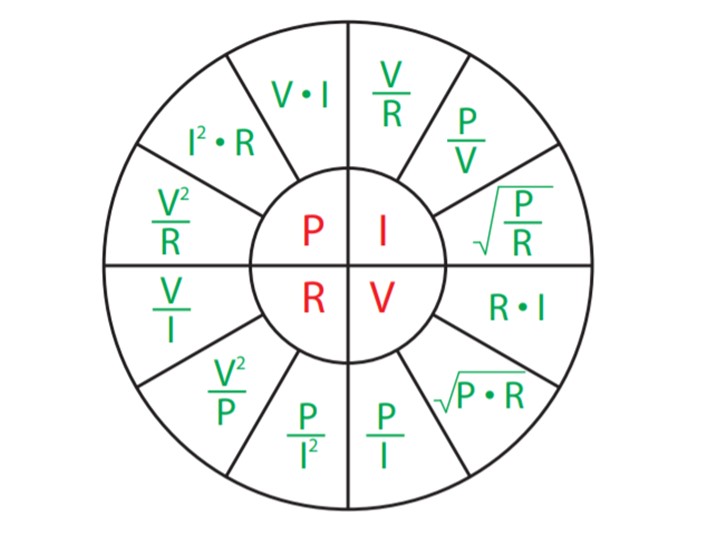
Las combinaciones posibles entre las cuatro magnitudes: potencia P, corriente I, voltaje V y resistencia R aparecen en la carta de la figura 5. Según los datos que ofrezca un problema, se eligen las fórmulas más convenientes.

Por ejemplo, supóngase que en un determinado problema se pide hallar la resistencia R, que está en el cuarto inferior izquierdo de la carta.

Dependiendo de las magnitudes cuyo valor se conozca, se elige alguna de las tres ecuaciones relacionadas (en color verde). Por ejemplo supongamos que se conocen V e I, entonces:

R = V/ I

Si en cambio se conocen P e I, y se pide la resistencia, se usa:

R = P / I²

Finalmente, cuando se conocen P y V, la resistencia se obtiene mediante:

R = P² /V

Aplicaciones

La ley de Watt puede aplicarse en circuitos eléctricos para encontrar la potencia eléctrica suministrada o consumida por el elemento. Los bombillos son buenos ejemplos de aplicación de la ley de Watt.

Ejemplo 1

Un bombillo especial para obtener varias iluminaciones en uno, posee dos filamentos de tungsteno, cuyas resistencias son R_A = 48 ohm y R_B = 144 ohm. Están conectadas a tres puntos, denotados como 1, 2 y 3, tal como se aprecia en la figura.

El dispositivo se controla mediante interruptores para seleccionar los pares de terminales y además conectarlo a la red de 120 V. Encontrar todas las posibles potencias que se pueden obtener.

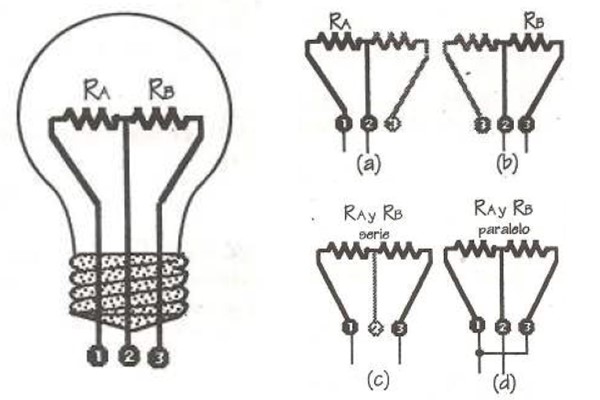
Solución

– Cuando se conectan los terminales 1 y 2, solamente la resistencia R_A queda activada. Ya que se tiene la tensión, que es de 120 V y el valor de la resistencia, se sustituyen directamente estos valores en la ecuación:

P = V²/R = (120 V)²/48 ohm = 300 W

– Conectando los terminales 2 y 3, se activa la resistencia R_B, cuya potencia es:

P = V²/R = (120 V)²/144 ohm = 100 W

– Los terminales 1 y 3 permiten que las resistencias queden conectadas en serie. La resistencia equivalente es:

R_eq = R_A + R_B = 48 ohm + 144 ohm = 192 ohm

Por lo tanto:

P = V²/R = (120 V)² /192 ohm = 75 W

– Finalmente, la posibilidad restante es conectar las resistencias en paralelo, tal como se muestra en el diagrama d). La resistencia equivalente en este caso es:

1/ R_eq = (1/R_A) + (1/R_B) =(1/48 ohm) + (1/144 ohm) = 1/36 ohm.

Por lo tanto la resistencia equivalente es R_eq = 36 ohm. Con este valor, la potencia es:

P = V² / R = (120 V)² / 36 ohm = 400 W

Ejemplo 2

Además del watt, otra unidad muy utilizada para la potencia es el kilowatt (o kilovatio), abreviada como kW. 1 kW equivale a 1000 watt.

Las compañías que abastecen de electricidad a los hogares facturan en términos de la energía consumida, no de la potencia. La unidad que emplean es el kilowatt-hora (kW-h) que pese a llevar el nombre de watt, es unidad para energía.

1 kilowatt-hora o kW-h es la energía suministrada en 1 hora mediante una potencia de 1000 watt, que en joules equivaldría a:

1 kW-h = 1000 W x 3600 s = 3.6 x 10 ⁶ J

a) Supongamos que un hogar consume 750 kWh durante un determinado mes. ¿Cuál será el monto de la factura de electricidad de ese mes? Se sigue el siguiente plan de consumo:

– Tarifa base: $14.00.

– Precio: 16 centavos/kWh hasta llegar a 100 kWh al mes.

– Los siguientes 200 kWh al mes tienen un valor de 10 centavos/kWh.

– Y por encima de 300 kWh al mes, se cobran 6 centavos/kWh.

b) Hallar el costo promedio de energía eléctrica.

Solución a

– El cliente consume 750 kW-h al mes, por lo tanto supera los costos indicados en cada etapa. Para los primeros 100 kWh el valor en dinero es: 100 kWh x 16 centavos /kWh = 1600 centavos = 16.00 $

– Los siguientes 200 kWh tienen un costo de: 200 kWh x 10 centavos /kWh = 2000 centavos = 20.00 $.

– Por encima de estos 300 kW-h, el cliente consume 450 kW-h más, para un total de 750 kW-h. El costo en este caso es: 450 kWh x 6 centavos /kWh = 2700 centavos = 27.00 $.

– Finalmente se suman todos los montos obtenidos más la tarifa de base, para obtener el precio del recibo de ese mes:

Precio a pagar = 14.00 $+ 16.00 $ +20.00 $+ 27.00 $ = 77 $.

Solución b

El costo promedio es: 77 $ / 750 kWh = 0.103 $ /kW-h = 10.3 centavos /kWh.

Referencias

1. Alexander, C. 2006. Fundamentos de circuitos eléctricos. 3ra. Edición. McGraw Hill.
2. Berdahl, E. Introduction to Electronics. Recobrado de: ccrma.stanford.ed.
3. Boylestad, R. 2011. Introducción al análisis de circuitos. 13va. Edición. Pearson.
4. Electrical Rebuilder’s Association. Ohm’s Law & Watt’s Law Calculator with Examples. Recobrado de: electricalrebuilders.org
5. Figueroa, D. (2005). Serie: Física para Ciencias e Ingeniería. Volumen 5. Electricidad. Editado por Douglas Figueroa (USB).