Ondas lineales: concepto, características, ejemplos
Las ondas lineales son aquellas en las que es aplicable el principio de superposición, es decir aquellas en que la forma de onda y su evolución espacio-temporal puede conseguirse como la sumatoria de soluciones básicas, por ejemplo de tipo armónico. No todas las ondas cumplen el principio de superposición, a las que no lo cumplen se les denomina ondas no-lineales.
La denominación “lineal” proviene del hecho de que las ondas lineales siempre satisfacen una ecuación diferencial en derivadas parciales, en la que todos los términos que involucran la variable dependiente o sus derivadas están elevados a la primera potencia.

Por su parte, las ondas no-lineales satisfacen ecuaciones de onda que poseen términos cuadráticos o de grados superiores en la variable dependiente o en sus derivadas.
En ocasiones se confunde a las ondas lineales con las ondas longitudinales, que son aquellas en las cuales la vibración ocurre en la misma dirección de la propagación, como las ondas sonoras.
Pero las ondas longitudinales, así como las transversales, pueden a su vez ser lineales o no-lineales dependiendo de, entre otros factores, la amplitud de la perturbación inicial y el medio en el que se propagan.
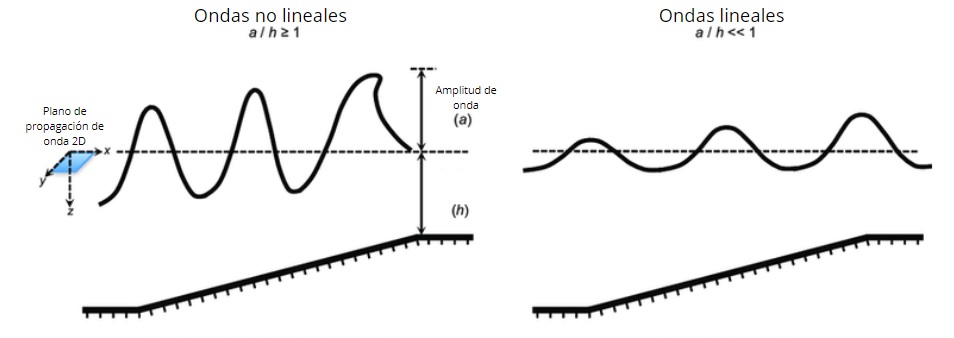
Generalmente ocurre que cuando la perturbación inicial es de pequeña amplitud, la ecuación que describe la propagación de la onda, es de tipo lineal o se puede linealizar mediante ciertas aproximaciones, aunque no siempre es así.
Índice del artículo
- 1 Ecuación diferencial en las ondas lineales
- 2 Ondas lineales dispersivas y no dispersivas
- 3 Ejemplos de ondas lineales
- 4 Referencias
En un medio lineal, una forma de onda limitada en espacio y tiempo puede representarse mediante la suma de funciones de onda de tipo seno o coseno de diferentes frecuencias y longitudes de ondas mediante series de Fourier.
Las ondas lineales siempre tienen asociada una ecuación diferencial del tipo lineal, cuya solución representa la predicción de lo que será la perturbación en instantes posteriores de una perturbación inicial localizada espacialmente en el instante inicial.
La ecuación de onda lineal clásica, en una sola dimensión espacial, cuyas soluciones son ondas lineales es:
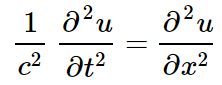
En la ecuación anterior u representa la perturbación de cierta cantidad física en la posición x y en el instante t, es decir u es una función de x y t:
u = u(x,t)
Por ejemplo, si se trata de una onda sonora en el aire, u puede representar la variación de la presión respecto de su valor sin perturbar.
En el caso de una onda electromagnética, u representa el campo eléctrico o el campo magnético oscilando perpendicularmente a la dirección de propagación.
Tratándose de una cuerda tensa, u representa el desplazamiento transversal respecto de la posición de equilibrio de la cuerda, tal como se muestra en la siguiente figura:

Si se tienen dos o más soluciones de la ecuación diferencial lineal, entonces cada solución multiplicada por una constante será solución y también lo será la suma de ellas.
A diferencia de las ecuaciones no-lineales, las ecuaciones lineales de onda admiten soluciones armónicas del tipo:
u1= A⋅sen(k⋅x – ω⋅t) y u2= A⋅sen(k⋅x + ω⋅t)
Esto puede verificarse por simple sustitución en la ecuación lineal de onda.
La primera solución representa una onda progresiva que avanza a la derecha, mientras que la segunda hacia la izquierda con rapidez c = ω/k.
Las soluciones armónicas son características de las ecuaciones de onda lineales.
Por otra parte, la combinación lineal de dos soluciones armónicas también es solución de la ecuación lineal de ondas, por ejemplo:
u = A1 cos(k1⋅x – ω1⋅t) + A2 sen(k2⋅x – ω2⋅t) es solución.
La característica más relevante de las ondas lineales, es que cualquier forma de onda, por compleja que sea, puede obtenerse mediante una sumatoria de ondas armónicas simples en seno y coseno:
u(x,t) = A0 + ∑n An cos(kn⋅x – ωn⋅t) + ∑m Bm sen(km⋅x – ωm⋅t).
En la ecuación de ondas lineal clásica, c representa la velocidad de propagación del pulso.
En los casos en los que c es un valor constante, por ejemplo las ondas electromagnéticas en el vacío, entonces un pulso en el instante inicial t=0 de la forma f(x) se propaga de acuerdo a:
u(x,t) = f(x – c⋅t)
Sin sufrir ninguna distorsión. Cuando esto ocurre, se dice que el medio es no-dispersivo.
Sin embargo, en los medios dispersivos la velocidad c de propagación puede depender de la longitud de onda λ, es decir: c = c(λ).
Las ondas electromagnéticas son dispersivas al viajar por un medio material. También las ondas superficiales del agua viajan a diferente velocidad según la profundidad del agua.
La velocidad con la que se propaga una onda armónica del tipo A⋅sen(k⋅x – ω⋅t) es ω/k = c y se denomina la velocidad de fase. Si el medio es dispersivo, entonces c es una función del número de onda k: c = c(k), donde k se relaciona con la longitud de onda mediante k = 2π/λ.
Relaciones de dispersión
La relación entre la frecuencia y la longitud de onda se llama la relación de dispersión, que expresada en términos de la frecuencia angular ω y el número de onda k es: ω = c(k)⋅k.
Algunas relaciones de dispersión características de ondas lineales son las siguientes:
En las olas de mar en las que la longitud de onda (distancia entre crestas) es mucho mayor que la profundidad H, pero que su amplitud es mucho menor que la profundidad la relación de dispersión es:
ω = √(gH)⋅k
De allí se concluye que se propagan a velocidad constante √(gH) (medio no dispersivo).
Pero las olas en aguas muy profundas si que son dispersivas, ya que su relación de dispersión es:
ω = √(g/k)⋅k
Esto significa que la velocidad de fase ω/k es variable y depende del número de onda y por tanto de la longitud de onda de la ola.
Velocidad de grupo
Si dos ondas lineales armónicas se superponen pero avanzan a velocidades distintas, entonces la velocidad de grupo (es decir, del paquete de ondas) no coincide con la velocidad de fase.
La velocidad de grupo vg se define como la derivada de la frecuencia respecto del número de onda en la relación de dispersión: vg = ω’(k).
La siguiente figura muestra la superposición o suma de dos ondas armónicas u1= A⋅sen(k1⋅x – ω1⋅t) y u2= A⋅sen(k2⋅x – ω2⋅t) que viajan a velocidades distintas v1= ω1/k1 y v2= ω2/k2. Nótese como la velocidad de grupo es diferente a la velocidad de fase, en este caso la velocidad de grupo es ∆ω/∆k.
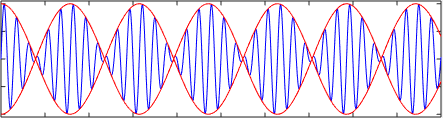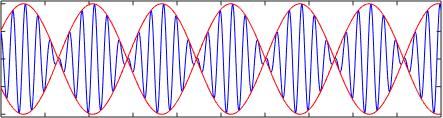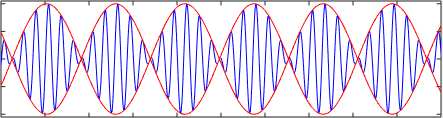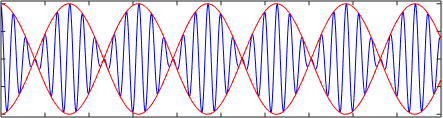
Dependiendo de la relación de dispersión puede ocurrir incluso que la velocidad de fase y la velocidad de grupo, en las ondas lineales, tengan direcciones opuestas.

Las ondas electromagnéticas son ondas lineales. Su ecuación de ondas se deduce a partir de las ecuaciones del electromagnetismo (ecuaciones de Maxwell) que también son lineales.
Es la ecuación que describe la dinámica de las partículas a escala atómica, donde las características ondulatorias son relevantes, por ejemplo el caso de los electrones en el átomo.
Entonces la “onda del electrón” o función de onda como también se le denomina, es una onda lineal.
También son ondas lineales aquellas en las que la amplitud es mucho menor a la longitud de onda y la longitud de onda mucho mayor que la profundidad. Las olas en aguas profundas siguen la teoría lineal (conocida como teoría ondulatoria de Airy).
Sin embargo, la ola que se acerca a la orilla y forma la característica cresta que se enrolla (y que le encanta a los surfistas) es una onda no lineal.
Como el sonido es una pequeña perturbación de la presión atmosférica, se considera una onda lineal. Sin embargo, la onda de choque de una explosión o el frente de onda de un avión supersónico, son ejemplos típicos de onda no lineal.
Las ondas que se propagan por una cuerda tensa son lineales, siempre que la pulsación inicial sea de pequeña amplitud, es decir que no se sobrepase el límite elástico de la cuerda.
Las ondas lineales en las cuerdas se reflejan en sus extremos y se superponen, dando lugar a ondas estacionarias o modos vibracionales que dan los tonos armónicos y subarmónicos característicos de los instrumentos de cuerda.
- Griffiths G and Schiesser W. Linear and Nonlinear Waves. Recuperado de: sholarpedia.org.
- Whitham G.B. (1999) “Linear and Nonlinear Waves”. Wiley.
- Wikipedia. Ondas no lineales. Recuperado de: es.wikipedia.com
- Wikipedia. Nonlinear acoustic. Recuperado de: en.wikipedia.com
- Wikipedia. Waves. Recuperado de: en.wikipedia.com
- Wikiwaves. Nonlinear waves. Recuperado de: wikiwaves.org
