Distribución normal: fórmula, características, ejemplo, ejercicio
La distribución normal o distribución gaussiana es la distribución de probabilidad en variable continua, en la que la función densidad de probabilidad está descrita por una función exponencial de argumento cuadrático y negativo, que da lugar a una forma acampanada.
El nombre de distribución normal viene del hecho que esta distribución es la que se aplica a mayor número de situaciones donde está involucrada alguna variable aleatoria continua en un grupo o población dada.
Como ejemplos donde se aplica la distribución normal se tienen: la altura de los hombres o de las mujeres, variaciones en la medida de alguna magnitud física o en rasgos psicológicos o sociológicos medibles como el cociente intelectual o los hábitos de consumo de cierto producto.
Por otra parte, se le llama distribución gaussiana o campana de Gauss, porque es a este genio matemático alemán a quién se le acredita su descubrimiento por el uso que le dio para la descripción del error estadístico de las mediciones astronómicas allá por el año 1800.
Sin embargo, se afirma que esta distribución estadística fue publicada previamente por otro gran matemático de origen francés, como lo fue Abraham de Moivre, allá por el año 1733.
Índice del artículo
- 1 Fórmula
- 2 Características de la distribucion normal
- 3 Aplicaciones de la distribución normal
- 4 Ejemplo
- 5 Ejercicio resuelto
- 6 Referencias
A la función distribución normal en la variable continua x, con parámetros μ y σ se le denota por:
N(x; μ,σ)
y explícitamente se escribe así:
N(x; μ,σ) = ∫-∞x f(s; μ,σ) ds
donde f(u; μ,σ) es la función densidad de probabilidad:
f(s; μ,σ) = (1/(σ√(2π)) Exp( – s2/(2σ2) )
La constante que multiplica a la función exponencial en la función densidad de probabilidad se le llama constante de normalización, y se ha elegido de tal manera que:
N(+∞, μ,σ) = 1
La expresión anterior asegura que la probabilidad de que la variable aleatoria x esté comprendida entre -∞ y +∞ sea 1, es decir el 100% de probabilidad.
El parámetro μ es la media aritmética de la variable aleatoria continua x y σ la desviación típica o raíz cuadrada de la varianza de esa misma variable. En el caso que μ = 0 y σ = 1 se tiene entonces la distribución normal estándar o distribución normal típica:
N( x; μ = 0, σ = 1)
1- Si una variable estadística aleatoria sigue una distribución normal de densidad de probabilidad f(s; μ,σ), la mayor parte de los datos se agrupan alrededor de valor medio μ y están dispersos a su alrededor de forma tal que poco más de ⅔ de los datos están entre μ – σ y μ + σ.
2- La desviación típica σ siempre es positiva.
3- La forma de la función de densidad f se asemeja a la de una campana, por lo que a esta función muchas veces se le llama campana de Gauss o función gaussiana.
4- En una distribución gaussiana la media, la mediana y la moda coinciden.
5- Los puntos de inflexión de la función densidad de probabilidad se encuentran justamente en μ – σ y μ + σ.
6- La función f es simétrica respecto a un eje que pase por su valor medio μ y tiene asintóticamente a cero para x ⟶ +∞ y x ⟶ -∞.
7- A mayor valor de σ mayor dispersión, ruido o distanciamiento de los datos alrededor del valor medio. Es decir a mayor σ la forma de campana es más abierta. En cambio σ pequeño indica que los dados se ciñen a la media y la forma de la campana es más cerrada o puntiaguda.
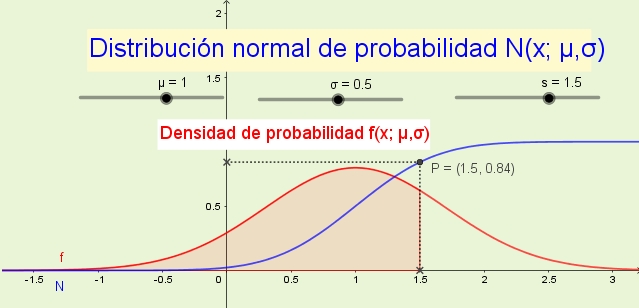
8- La función de distribución N(x; μ,σ) indica la probabilidad que la variable aleatoria sea menor o igual que x. Por ejemplo, en la figura 1 (más arriba) la probabilidad P de que la variable x sea menor o igual a 1.5 es de 84% y se corresponde con el área bajo la función densidad de probabilidad f(x; μ,σ) desde -∞ hasta x.
9- Si los datos siguen una distribución normal, entonces 68,26% de estos están entre μ – σ y μ + σ.
10- El 95,44% de los datos que siguen una distribución normal se encuentran entre μ – 2σ y μ + 2σ.
11- El 99,74% de los datos que siguen una distribución normal se encuentran entre μ – 3σ y μ + 3σ.
12- Si una variable aleatoria x sigue una distribución N(x; μ,σ), entonces la variable
z = (x – μ) / σ sigue la distribución normal estándar N(z; 0,1).
El cambio de la variable x a la z recibe el nombre de estandarización o tipificación y es de gran utilidad a al momento de aplicar las tablas de la distribución estándar a los datos que siguen una distribución normal no-estándar.
Para aplicar la distribución normal es necesario pasar por el cálculo de la integral de la densidad de probabilidad, lo cual desde el punto de vista analítico no es fácil y no siempre se dispone de un programa informático que permita su cálculo numérico. Para este fin se usan las tablas de valores normalizados o tipificados, que no es más que la distribución normal en el caso μ =0 y σ =1.
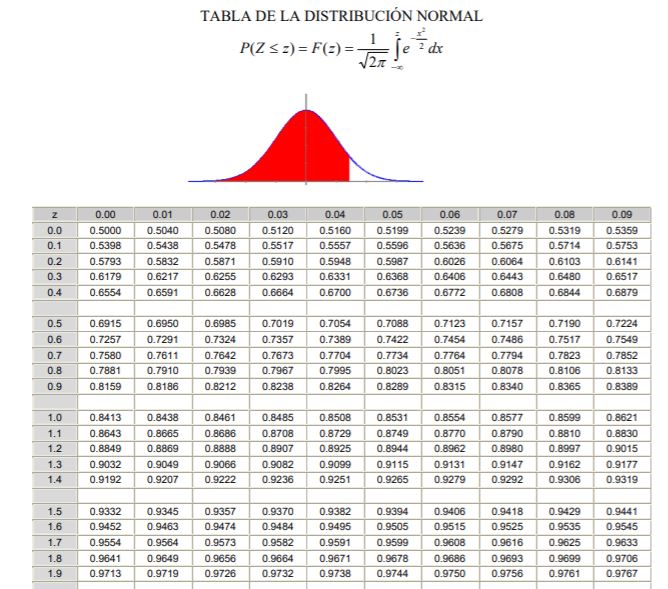
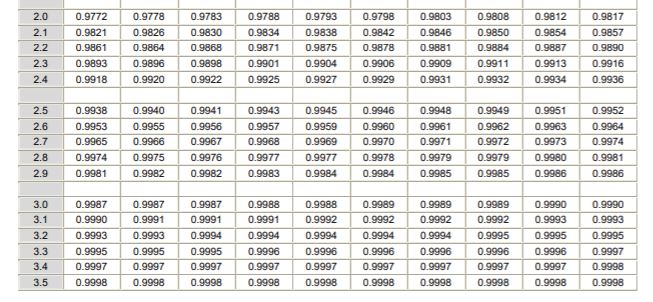
Debe notarse que estas tablas no incluyen los valores negativos. Sin embargo, usando las propiedades de simetría de la función densidad de probabilidad gaussiana pueden obtenerse los valores correspondientes. En el ejercicio resuelto mostrado más abajo se indica el uso de la tabla en estos casos.
Suponga que tiene un conjunto de datos aleatorios x que siguen una distribución normal de media 10 y desviación típica 2. Se pide encontrar la probabilidad de que:
a) La variable aleatoria x sea menor o igual a 8.
b) Sea menor o igual a 10.
c) Que la variable x esté por debajo de 12.
d) La probabilidad que un valor x esté entre 8 y 12.
Solución:
a) Para responder a la primera pregunta simplemente hay que calcular:
N(x; μ,σ)
Con x = 8, μ = 10 y σ = 2. Nos percatamos que se trata de una integral que no tiene una solución analítica en funciones elementales, sino la solución está expresada en función de la función error erf(x).
Por otra parte, existe la posibilidad de resolver la integral en forma numérica, que es lo que hacen muchas calculadoras, las hojas de cálculo y programas informáticos como GeoGebra. La siguiente figura muestra la solución numérica correspondiente al primer caso:
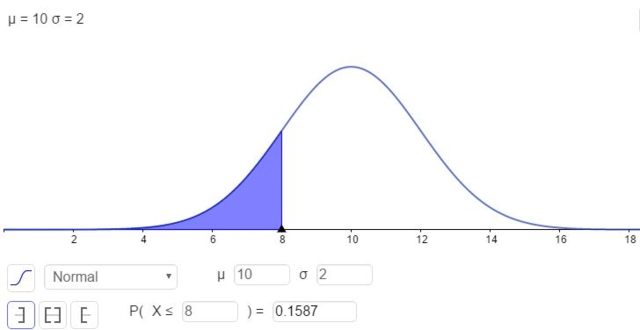
y la respuesta es que la probabilidad que x esté por debajo de 8 es:
P( x ≤ 8 ) = N(x=8; μ=10,σ=2) = 0,1587
b) En este caso se trata de encontrar la probabilidad de que la variable aleatoria x esté por debajo de la media que en este caso vale 10. La respuesta no requiere cálculo alguno, ya que sabemos que la mitad de los datos están por debajo de la media y la otra mitad por encima de la media. Por ello, la respuesta es:
P( x ≤ 10 ) = N(x=10; μ=10,σ=2) = 0,5
c) Para responder a esta pregunta hay que calcular N(x=12; μ=10,σ=2), lo cual puede hacerse con una calculadora que tenga funciones estadísticas o mediante un software como es el caso de GeoGebra:
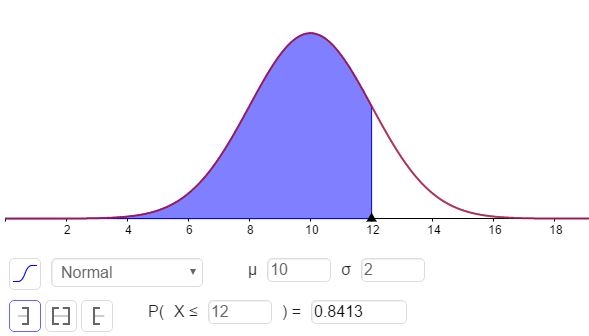
La respuesta a la parte c puede verse en la figura 3 y es:
P( x ≤ 12 ) = N(x=12; μ=10,σ=2) = 0,8413.
d) Para encontrar la probabilidad de que la variable aleatoria x esté comprendida entre 8 y 12 podemos usar los resultados de las partes a y c de la siguiente manera:
P( 8 ≤ x ≤ 12 ) = P( x ≤ 12 ) – P( x ≤ 8 ) = 0,8413 – 0,1587 = 0,6826 = 68,26 %.
El precio promedio de las acciones de una empresa es de $25 con una desviación típica de $4. Determine la probabilidad que:
a) Una acción tenga un costo menor de $20.
b) Que tenga un costo mayor de $30.
c) El precio esté comprendido entre $20 y $30.
Usar las tablas de distribución normal tipificada para encontrar las respuestas.
Solución:
Para poder hacer uso de las tablas, es necesario pasar a la variable z normalizada o tipificada:
$20 en la variable normalizada equivale a z = ($20 – $25) / $4 = -5/4 = -1,25 y
$30 en la variable normalizada equivale a z = ($30 – $25) / $4 = +5/4 = +1,25.
a) $20 equivale a -1,25 en la variable normalizada, pero la tabla no tiene valores negativos, por lo que ubicamos el valor +1,25 que arroja el valor de 0,8944.
Si a este valor se le resta 0,5 el resultado será el área entre 0 y 1,25 que, por cierto, es idéntica (por simetría) al área entre -1.25 y 0. El resultado de la resta es 0,8944 – 0,5 = 0,3944 que es el área entre -1.25 y 0.
Pero interesa el área desde -∞ hasta -1,25 que será 0,5 – 0,3944 = 0,1056. Se concluye por tanto que la probabilidad que una acción esté por debajo de $20 es 10,56%.
b) $30 en la variable tipificada z es 1,25. Para este valor en la tabla aparece el número 0,8944 que corresponde al área desde -∞ hasta +1,25. El área entre +1.25 y +∞ es (1 – 0,8944) = 0,1056. Es decir que la probabilidad que una acción cueste más de $30 es 10,56%.
c) La probabilidad de que una acción tenga un costo comprendido entre $20 y $30 se calculará así:
100% -10,56% – 10,56% = 78,88%
- Estadística y probabilidad. Distribución normal. Recuperado de: proyectodescartes.org
- Geogebra. Geogebra clásico, cálculo de probabilidad. Recuperado de geogebra.org
- MathWorks. Distribución de Gauss. Recuperado de: es.mathworks.com
- Mendenhall, W. 1981. Estadística para Administración y Economía. 3ra. edición. Grupo Editorial Iberoamérica.
- Stat Trek. Teach yourself Statistics. Poisson Distribution. Recuperado de: stattrek.com,
- Triola, M. 2012. Elementary Statistics. 11th. Ed. Pearson Education.
- Universidad de Vigo. Principales distribuciones continuas. Recuperado de: anapg.webs.uvigo.es
- Wikipedia. Distribución normal. Recuperado de: es.wikipedia.org
