Proceso politrópico: características, aplicaciones y ejemplos

Un proceso politrópico es un proceso termodinámico que ocurre cuando la relación entre la presión P y el volumenV dada por P.Vⁿ se mantiene constante. El exponente n es un número real, generalmente comprendido entre cero e infinito, pero que en algunos casos puede ser negativo.

El valor de n recibe el nombre de índice de politropía y es importante resaltar que durante un proceso termodinámico politrópico dicho índice debe mantener un valor fijo, de lo contrario el proceso no se considerará politrópico.

Índice del artículo

• 1 Características de los procesos politrópicos
• 2 Aplicaciones
  • 2.1 Trabajo en procesos politrópicos para distintos valores de n
• 3 Ejemplos de procesos politrópicos
  • 3.1 – Ejemplo 1
  • 3.2 – Ejemplo 2
• 4 Referencias

Características de los procesos politrópicos

Algunos casos característicos de procesos politrópicos son: 

– El proceso isotérmico (a temperatura T constante), en el que el exponente es n=1.

– Un proceso isobárico (a presión P constante), en este caso n=0.

– El proceso isocórico (a volumen V constante), para el cual n=+∞.

– Los procesos adiabáticos (a entropía S constante), en los cuales el exponente es n=γ, siendo γ la constante adiabática. Esta constante es el cociente entre la capacidad calorífica a presión constante Cp dividido entre la capacidad calorífica a volumen constante Cv:

γ=Cp/Cv

– Cualquier otro proceso termodinámico que no sea alguno de los casos anteriores. pero que cumpla P.Vⁿ = ctte con índice politrópico real y constante n será también un proceso politrópico.

Aplicaciones

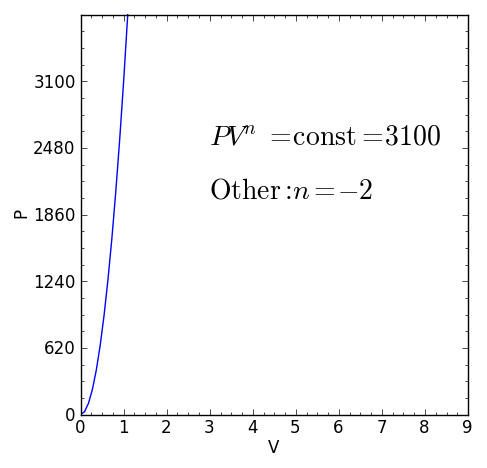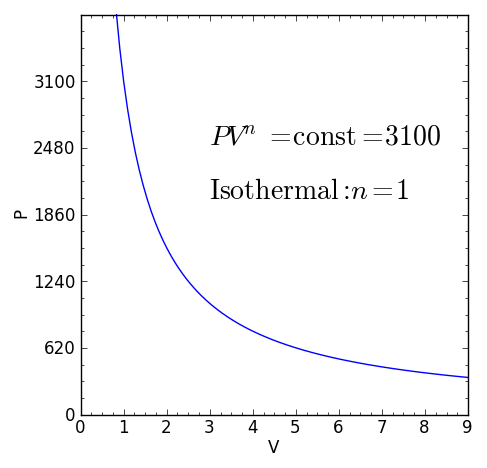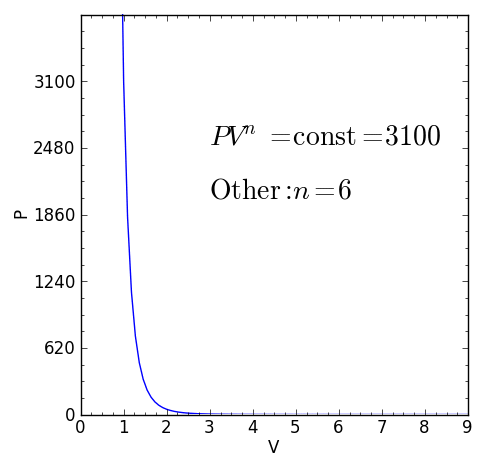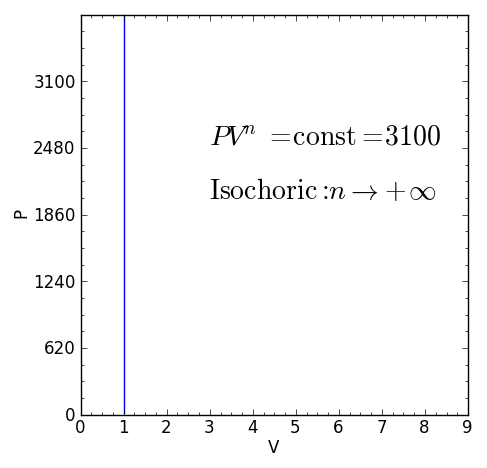
Una de las principales aplicaciones de la ecuación politrópica es para el cálculo del trabajo realizado por un sistema termodinámico cerrado, cuando pasa de un estado inicial a otro  final en forma cuasiestática, es decir, siguiendo una sucesión de estados de equilibrio.

Trabajo en procesos politrópicos para distintos valores de n

Para n≠1

El trabajo mecánico W realizado por un sistema termodinámico cerrado se calcula mediante la expresión:

W = ∫P.dV

Donde P es la presión y V el volumen.

Como en el caso de un proceso politrópico la relación entre la presión y el volumen es:

P.V ⁿ = constante =C

Despejando P de la expresión anterior para sustituirla en la expresión del trabajo:

P = C /V ⁿ

Se tiene el trabajo mecánico realizado durante un proceso politrópico, el cual comienza en un estado inicial 1 y termina en el estado final 2. Todo esto aparece en la siguiente expresión:

C = P₁ V₁ⁿ = P₂ V₂ⁿ

Al sustituir el valor de la constante en la expresión del trabajo se obtiene:

W = (P₂ V₂ – P₁ V₁)/(1-n)

En el caso que la sustancia de trabajo pueda modelarse como un gas ideal, se tiene la siguiente ecuación de estado:

P.V = m.R.T

Donde m es el número de moles del gas ideal y R es la constante universal de los gases.

Para un gas ideal que sigue un proceso politrópico con indice de politropía diferente de la unidad y que pasa de un estado con temperatura inicial T₁ a otro estado con temperatura T₂ se tiene que el trabajo efectuado está dado por la siguiente fórmula:

W = m R (T₂ – T₁)/(1-n)

Para n → ∞

De acuerdo a la fórmula para el trabajo obtenida en la sección previa, se tiene que el trabajo de un proceso politrópico con n = ∞ es nulo, debido a que la expresión del trabajo queda dividida entre el infinito y por tanto el resultado tiende a cero.

Otra forma de llegar a este resultado es partir de la relación P₁ V₁ⁿ = P₂ V₂ⁿ, la cual puede ser reescrita de la siguiente manera:

(P₁/P₂) = (V₂/V1)ⁿ

Tomando raíz n-ésima en cada miembro se obtiene:

(V₂/V1) = (P₁/P₂)^(1/n)

En el caso que n → ∞, se tiene que (V₂/V1)=1, lo que significa que:

V₂ = V₁

Es decir, el volumen no cambia en un proceso politrópico con n → ∞. Por tanto el diferencial de volumen dV en la integral del trabajo mecánico es 0. A este tipo de procesos politrópicos se les conoce también como procesos isocóricos, o procesos a volumen constante.

Para n = 1

Nuevamente tenemos la expresión la expresión para el trabajo:

W = ∫P dV

En el caso de un proceso politrópico con n = 1, la relación entre la presión y el volumen es:

P V = constante= C

Al despejar P de la expresión anterior y sustituir, se tiene el trabajo realizado para ir desde el estado inicial 1 hasta el estado final 2:

Es decir:

W = C ln(V₂/V₁).

Como los estados inicial y final están bien determinados, también lo estará la ctte. Es decir:

C= P₁ V₁ = P₂ V₂

Finalmente se tienen las siguientes expresiones útiles para hallar el trabajo mecánico de un sistema cerrado politrópico en el que n=1.

W= P₁ V₁ ln(V₂/V₁) = P₂ V₂ ln(V₂/V₁)

Si la sustancia de trabajo consta de m moles de gas ideal, entonces puede aplicarse la ecuación de estado del gas ideal: P V = m.R.T.

En este caso, como P.V₁ = ctte, se tiene que un proceso politrópico con n=1 es un proceso a temperatura T constante (isotérmico), de modo que pueden obtenerse las siguientes expresiones para el trabajo:

W = m R T₁ ln(V₂/V₁) = m R T₂ ln(V₂/V₁)

Ejemplos de procesos politrópicos

– Ejemplo 1

Suponga un cilindro con un pistón movible lleno con un kilogramo de aire. Inicialmente el aire ocupa un volumen V₁= 0,2 m³ a una presión P₁= 400 kPa. Se sigue un proceso politrópico con n=γ=1,4, cuyo estado final tiene presión P₂ = 100 kPa. Determine el trabajo efectuado por el aire sobre el pistón.

Solución

Cuando el índice de politropía se iguala a la constante adiabática, se tiene un proceso en el cual la sustancia de trabajo (el aire) no intercambia calor con el entorno, y por tanto tampoco cambia la entropía.

Para el aire, un gas ideal diatómico, se tiene:

γ = Cp/Cv, con Cp = (7/2)R y Cv = (5/2)R

Entonces:

γ = 7/5 = 1,4

Usando la expresión del proceso politrópico puede determinarse el volumen final del aire:

V₂ = [(P₂ V₁^1,4)/P₂]^(1/1,4) = 0,54 m³.

Ahora se tienen las condiciones para aplicar la fórmula del trabajo realizado en un proceso politrópico para n≠1 obtenida más arriba:

W = (P₂ V₂ – P1 V1)/(1-n)

Sustituyendo los valores apropiados se tiene:

W = (100 kPa 0,54 m³ – 400 kPa 0,2 m³)/(1 – 1,4) = 65,4 kJ

– Ejemplo 2

Suponga el mismo cilindro del ejemplo 1, con un pistón movible lleno con un kilogramo de aire. Inicialmente el aire ocupa un volumen V1= 0,2 m³ a una presión P1= 400 kPa. Pero a diferencia del caso anterior el aire se expande isotérmicamente para llegar a una presión final P2 = 100 kPa. Determinar el trabajo efectuado por el aire sobre el pistón.

Solución

Como se ha visto anteriormente, los procesos isotérmicos son procesos politrópicos con índice n=1, por lo que se cumple que:

P1 V1 = P2 V2

De esta forma puede despegarse fácilmente el volumen final para obtener:

V2 = 0,8 m³

Entonces usando la expresión del trabajo obtenida previamente para el caso n=1 se tiene que el trabajo efectuado por el aire sobre el pistón en este proceso es:

W= P1 V1 ln(V2/V1) = 400000 Pa × 0,2 m³ ln(0,8/0,2) = 110,9 kJ.  

Referencias

1. Bauer, W. 2011. Física para Ingeniería y Ciencias. Volumen 1. Mc Graw Hill.
2. Cengel, Y. 2012. Termodinámica. 7ma Edición. McGraw Hill.
3. Figueroa, D. (2005). Serie: Física para Ciencias e Ingeniería. Volumen 4. Fluidos y Termodinámica. Editado por Douglas Figueroa (USB).
4. López, C. La Primera Ley de la Termodinámica. Recobrado de: culturacientifica.com.
5. Knight, R. 2017. Physics for Scientists and Engineering: a Strategy Approach. Pearson.
6. Serway, R., Vulle, C. 2011. Fundamentos de Física. 9na Ed. Cengage Learning.
7. Universidad de Sevilla. Máquinas Térmicas. Recobrado de: laplace.us.es.
8. Wikiwand. Proceso politrópico. Recobrado de: wikiwand.com.