Funciones matemáticas: qué son, variables, tipos, ejemplos
¿Qué son las funciones matemáticas?
Las funciones matemáticas son la expresión en lenguaje matemático de una relación entre dos variables, y el valor de la primera de las variables depende de la segunda. Normalmente, estas variables se simbolizan con las letras X e Y. A la variable X se le llama dominio o variable independiente; y a la Y, codominio o variable dependiente.
Veamos un ejemplo. Tenemos dos variables o magnitudes: dólar y centavos de dólar. Sabemos que 100 centavos de dólar son equivalentes a un dólar. Por tanto, centavos de dólar (X) es el dominio y dólar (Y) corresponde al codominio. Esta relación podemos expresarla con la siguiente función (F):
F(X) = Y / 100
Si tengo en mi hucha 143 centavos de dólar, y deseo saber cuántos dólares he ahorrado, solo aplico la función:
F(X) = 143 / 100
Por lo tanto, poseo 1,43 dólares.
También podemos expresar la relación inversa, es decir, que un dólar es equivalente a 100 centavos. En consecuencia, las categorías de las variables se invierten: dólar (X) pasa a ser el dominio mientras que centavos de dólar es el codominio. Lo expresamos de esta manera:
F(X) = X x 100
Si en mi hucha tengo 1,43 dólares, pero deseo saber a cuántos centavos equivale esta cifra, basta con aplicar esta segunda función.
F(X): 1,43 x 100
El resultado me devuelve a mis 143 centavos originales.
Las variables de las funciones matemáticas
Una variable es simplemente un símbolo (X, Y, Z) que representa una variedad de elementos.
En el ejemplo anterior, las variables X e Y simbolizaban al dólar y al centavo de dólar. Pero los mismos símbolos (X e Y) pueden ser utilizados para representar una infinidad de elementos, como por ejemplo: edad de una persona y su peso; número de vuelos a un determinado destino y un período de tiempo (por semana, por mes, por año), etc.
Las variables pueden clasificarse en numerosos tipos, pero los más relevantes para las funciones matemáticas son los siguientes:
- Variable dependiente: aquellas cuyo valor depende del valor que se asigne a otras variables dentro de la función.
- Variable independiente: los cambios en este tipo de variable influyen en los valores del resto de las variables de la función.
- Variable cuantitativa: se expresa mediante cantidades numéricas definidas. Pueden ser números enteros o decimales.
Características de las funciones matemáticas
1- La relación entre las variables se expresa en términos de equivalencia.
2- Para cada valor de la variable X existe un, y solo un equivalente de la variable Y. Y viceversa: para un determinado valor de Y existe un, y solo un resultado de la variable X.
3- Pueden ser representadas gráficamente sobre un plano cartesiano, lo cual permite predecir el comportamiento de una de las variables a partir de la otra.
4- La definición moderna de función matemática se debe al matemático alemán Peter Dirichlet (1805-1859), quien la publicó en 1837.
Tipos de funciones matemáticas
Las funciones matemáticas pueden ser clasificadas de acuerdo con distintos criterios, como la relación que se establece entre las variables X e Y o el comportamiento matemático de la función.
Entre los principales tipos están los siguientes:
Funciones algebraicas
Se caracterizan por establecer una relación entre componentes que se expresan bien sea a través de un monomio o de un polinomio. Esta relación puede ser determinada a través de operaciones matemáticas simples, como resta, multiplicación, división, suma, potenciación o radicación.
Funciones lineales
Al ser representadas sobre un plano cartesiano aparecen con la forma de una línea recta que corta el eje de coordenadas en un cierto punto. De ahí su nombre, aunque también se les conoce como funciones de primer grado.
Funciones a trozos
En este tipo el valor del codominio Y altera el comportamiento de la función. Se generan, por tanto, dos intervalos con diferente comportamiento en relación con el valor del dominio.
Funciones trascendentes
Son funciones altamente complejas. No bastan las operaciones algebraicas comunes (resta, multiplicación, división, suma, potenciación o radicación) para determinar la relación entre las variables, por lo cual se debe recurrir a otras herramientas matemáticas, como las derivadas, integrales o logaritmos.
Funciones trigonométricas
Este tipo de funciones muestran la relación numérica que existe entre los diversos elementos de un triángulo y otras figuras geométricas, especialmente entre sus ángulos. Las fórmulas para el seno, coseno, tangente, secante y cosecante son ejemplos de este tipo de funciones.
Funciones inyectivas
Las funciones de este tipo se caracterizan por la particularidad de la relación entre dominio y codominio. A cada uno de los valores de este último corresponde solo un valor del dominio. También puede suceder que un valor del dominio no posea ningún valor correspondiente en el codominio.
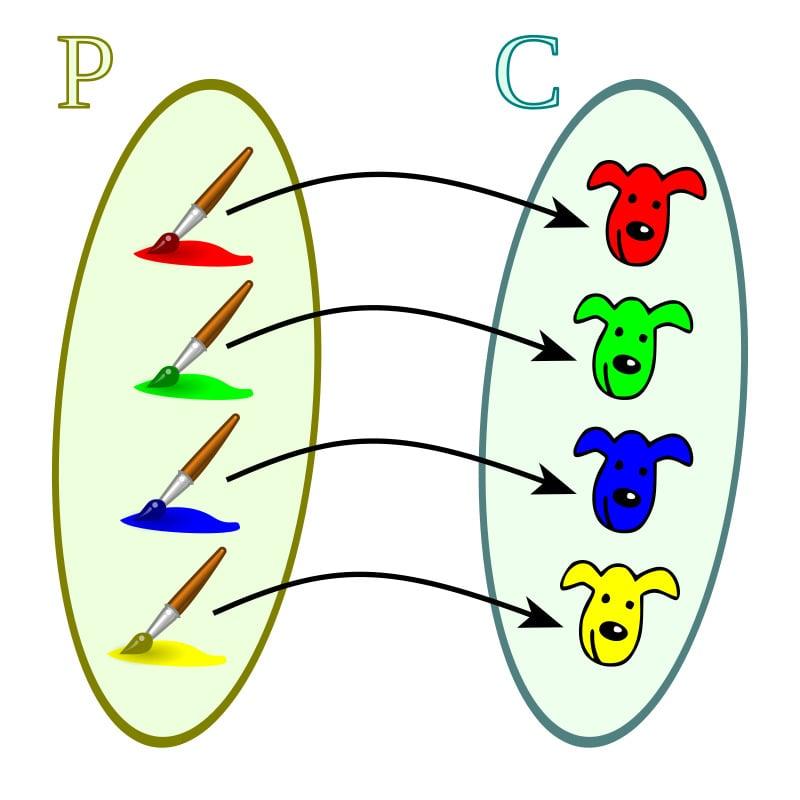
Funciones sobreyectivas
En este caso cada uno de las magnitudes del codominio tiene relación con al menos uno de los valores del dominio. Se distinguen de las funciones inyectivas en que los valores del codominio pueden estar relacionados con más de uno de los valores del dominio.
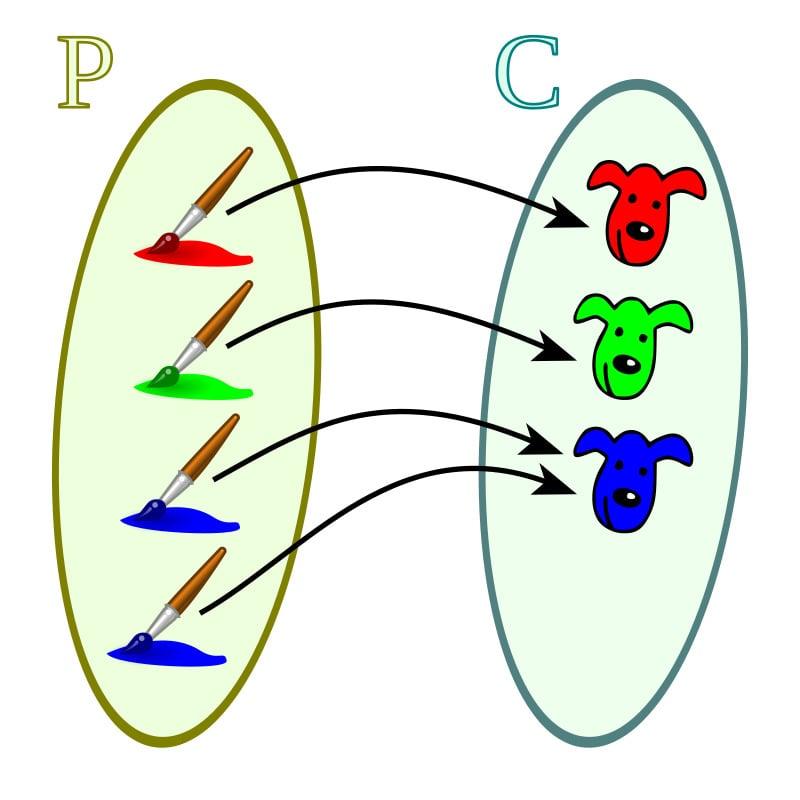
Funciones biyectivas
Este tipo de funciones presenta propiedades tanto inyectivas como sobreyectivas.
¿Para qué sirven las funciones matemáticas?
Las funciones son ampliamente usadas en todas las ciencias que tienen a la matemática como ciencia auxiliar. Es el caso de la física, la ingeniería, la medicina, las finanzas, la estadística, entre muchas otras.
En la vida cotidiana
Sin embargo, también pueden sernos útiles para resolver problemas más sencillos del día a día.
Imagina que tu abuelo te ha regalado 10 monedas, que gastarás en chocolatinas. En el quiosco, le has entregado las 10 monedas al dependiente, diciéndole que te dé todas las chocolatinas que se pueden comprar con esa cantidad de monedas. Te han dado 5 chocolatinas. ¿Cuál es el precio de cada una?
Planteamos el problema: si 5 chocolatinas equivalen a 10 monedas, entonces ¿a cuántas monedas equivale una sola chocolatina?
Nuestra variable independiente (X) es la cantidad de chocolatinas (5), mientras que a la variable dependiente (Y) corresponde el número de monedas, es decir, 10.
Expresamos la función de la siguiente manera:
F(X) = 2X/X
F(X) = 2(5)/5
F(X) = 10/5
F(X) = 2
Y ya tenemos la respuesta: cada chocolatina cuesta 2 monedas.
Referencias
- (2021). Functions and Equations. Tomado de encyclopedia.com.
- (s/f). Elementary Functions. The Mathematical Functions Site. Tomado de unctions.wolfram.com.
- (s/f). What is a Function? Tomado de mathsisfun.com.
- Britannica, The Editors of Encyclopaedia (2021). Function. Encyclopedia Britannica. Tomado de britannica.com.
- Castel, F. (s/f). Los 13 tipos de funciones matemáticas (y sus características). Tomado de psicologiaymente.com.
